
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение намагничивающего токаСодержание книги Поиск на нашем сайте
Fц=61,7+127,68+50,4+6,73+338,34=584,85 [А].
Эти падения магнитного напряжения соответствуют расчетному потоку полюса: Ф=0,0054 [Вб]. Провести магнитный поток по участкам позволяет магнитодвижущая сила обмотки статора, которая определяется произведением тока намагничивания Iм и числа витков обмотки w1. Наибольшее падение магнитного напряжения приходится на воздушный зазор: Fб/ Fц=338,34/584,85=0,578; практически это соотношение у проектируемых машин составляет от 60 до 90%; соотношение для проектируемого двигателя соответствует принятому для машин. Необходимый намагничивающий ток обмотки статора находим из выражения Iм Относительное значение намагничивающего тока:
Рекомендуемое соотношение для этих токов от 0,2 до 0,35; размеры и обмотки рассчитаны, верно, допустимые соотношения соблюдены. Ток холостого хода обмотки статора: I01=I0=Iм=2 [А].
3 Расчет активного сопротивления фазы обмотки статора
Схема замещения фазы асинхронной машины и уравнения, описывающие соотношения между токами и напряжениями в ней, отражают физические процессы, происходящие в фазе машины. Зная параметры схемы замещения, можно рассчитывать любые режимы работы двигателя. Двигатель с вращающимся ротором сведен к неподвижной схеме, где вращение учтено в приведенном активном сопротивлении фазы ротора. На рис.15 приведена схема замещения фазы. Параметры схемы замещения остаются неизменными при различных режимах работы машины: в пределах изменения скольжения от холостого хода до Sном их изменением можно пренебречь. При расчете пусковых характеристик происходит изменение параметров, из-за насыщения стали магнитопровода. Активное сопротивление фазы обмотки статора найдем из выражения: R1
lл l1ср=2*(0,13299+0,09165)=0.449[м]; L1=0,449*570=256[м]. Отсюда R1=256/(57*106*0,785*10-6)=5,68 [Ом].
Расчет активного сопротивления фазы короткозамкнутого ротора
К фазе обмотки ротора относится один стержень с сопротивлением Rс и две прилежащих к нему части короткозамыкающего кольца с сопротивлением Rк. Активное сопротивление фазы обмотки короткозамкнутого ротора найдем: R2=Rс+2Rк/[2sin(p*p/z2)]2 [Ом]; сопротивление стержня – Rс= Rк=p*Dkcp* Dkcp=D2-hп2=208,58-42=166,58 [мм]; 2Rк/[2sin(p*p/z2)]2=2*2*10-6/[2*sin(180*5/110)]2=49,4*10-6 [Oм]. Сопротивление стержня Rс=0,13299/30*106*78*10-6=56,83*10-6 [Ом]. Отсюда: R2=56,83*10-6+49,4*10-6=106,23*10-6 [Ом]. Приведенное активное сопротивление ротора: R21= R2*4m1(w1*K01)2/Z2[Ом]; R21=R2*K; K=m1(w1*K01)2/m2(w2*K02)2=m1(w1*K01)2/Z2(1/2*1)2=4*m1(w1*K01)2/Z2= =4*3*(570*0,91)2/110=29350,87 [Ом]; R21=3,12 [Ом].
Расчет индуктивного сопротивления фазы обмотки статора
Индуктивное сопротивление фазы обмотки статора найдем из выражения: X1=15.8*f/100*(w1/100)2*l1/p*q1*(aп1+ал1+Xg1)[Ом], где q1- число пазов фазы под одним полюсом; a- коэффициент магнитной проводимости пазового, лобового и дифференциального рассеяния (
hш=0,7[мм];
Для лобовой магнитной проводимости: Для дифференциальной проводимости: б=208,75*10-3 [мм]; Kб=1,23; Отсюда:
X1=15,8*50/100*(570/100)2*0,13299/5*3*(22,58+1,02+2,6)=0,086 [Ом].
Расчет индуктивного сопротивления обмотки ротора
Индуктивное сопротивление обмотки короткозамкнутого ротора найдем из выражения: X2=7,9*f1*l2*10-6*( Для лобовой проводимости: D2 =Dк=208,58 [мм]; Z2=110; l2=132,99 [мм]; аk=1,56 [мм]; 2sin(p*p/z2)=0,28;
Для дифференциальной проводимости: X2=7,9*50*0,13299*10-6*(5,83+1,1+2,37)=0,488*10-3 [Ом]. Приведенное сопротивление рассеяния фазы ротора: X21= X2*4*m1(w1*K01) 2/Z2=0,488*10-3*4*3*(570*0,91)2/110=14,32 [Ом]
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.163.43 (0.006 с.) |

 Расчет магнитной цепи машины проводим для режима холостого хода. Расчет провели с целью определения суммарного падения магнитного напряжения в замкнутом контуре магнитной цепи:
Расчет магнитной цепи машины проводим для режима холостого хода. Расчет провели с целью определения суммарного падения магнитного напряжения в замкнутом контуре магнитной цепи: [A].
[A]. .
. РАСЧЕТ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ФАЗЫ МАШИНЫ
РАСЧЕТ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ФАЗЫ МАШИНЫ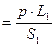 [Ом], где удельное сопротивление материала провода обмотки –
[Ом], где удельное сопротивление материала провода обмотки – =1/57*106 [Ом*м] для меди при расчетной температуре в [0С]; общая длина эффективных проводников в фазе обмотки статора - L1=l1ср*w1[м]; l1ср- средняя длина одного витка; l1ср=2(l1 +lл); lл – длина лобовой части секции;
=1/57*106 [Ом*м] для меди при расчетной температуре в [0С]; общая длина эффективных проводников в фазе обмотки статора - L1=l1ср*w1[м]; l1ср- средняя длина одного витка; l1ср=2(l1 +lл); lл – длина лобовой части секции;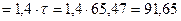 [мм];
[мм]; c*l2/Sc[Ом]; для литой обмотки ротора из алюминия – 1/
c*l2/Sc[Ом]; для литой обмотки ротора из алюминия – 1/ 
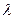 п1,
п1, 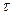 ); l1=132,99 [мм];
); l1=132,99 [мм];  b21/8 Sc)2+0.96; h1=40 [мм]; b1 =3 [мм]; Sc=78 [мм2];
b21/8 Sc)2+0.96; h1=40 [мм]; b1 =3 [мм]; Sc=78 [мм2]; 


