
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели формы распределенияСодержание книги
Поиск на нашем сайте Показатель асимметрии для сгруппированных данных находится из выражения
а показатель эксцесса:
Их относительные значения вычислены по формулам (7) и (10) и реализованы в ячейках В99 и В100. Формулы (31 и 32) записаны в ячейки В97 и В98. Проверка соответствия эмпирического распределения активов банков нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова 1. Критерий Пирсона
где Теоретические частоты вычисляются с помощью функции = 48*$B$83*НОРМРАСП(V3:V7; $В$84;$В$89;0). Формула (33) реализована в ячейке В101 =СУММПРОИЗВ (СТЕПЕНЬ (W3:W7-AF3:AF7; 2)/(AF3:AF7)). В ячейке В102 помещена формула Ячейка В103 содержит формулу = ХИ2РАСП(В101;В102) – вычисляет значение вероятности Другой подход к решению задачи основан на проверке попадания
Для вычисления Диаграмма эмпирических и теоретических частот приведена на рис. 9.
Рисунок 9 2. Критерий Романовского
Расчетное значение критерия равно 0,43, следовательно, расхождения теоретических и эмпирических частот являются случайными и несущественными. 3. Критерий Колмогорова ( Основан на определении максимального (по модулю) расхождения между накопленными частостями эмпирического и теоретического распределений (d):
Значения ВЫВОДЫ 1. В качестве характеристики центра распределения необходимо использовать среднюю арифметическую, т.к. совокупность является однородной (коэффициент вариации равен 10,87%, что менее 33%). 2. Степень дифференциации активов банков слабая. 3. Концентрация активов банков практически отсутствует. 4. Распределение активов банков плосковершинно и имеет правостороннюю асимметрию. Отклонения эмпирических частот от теоретических носят случайный характер, следовательно, эмпирическое распределение активов банков не противоречит нормальному.
ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ СРЕДНЕЙ ВЕЛИЧИНЫ АКТИВОВ БАНКОВ В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ Величина доверительного интервала (предельная ошибка выборки) находится из выражения
где t – коэффициент доверия;
Средняя ошибка бесповторной выборки:
где
N – объем генеральной совокупности. Дисперсия генеральной совокупности связана с выборочной дисперсией следующим отношением:
Следовательно, среднюю ошибку выборки можно представить выражением:
Коэффициент доверия в распределении Гаусса является только функцией доверительной вероятности, а в распределении Стьюдента, кроме того, еще и функцией объема выборки. Следовательно, для одной и той же доверительной вероятности можно получить два значения предельной ошибки.
Указанные значения приведены в ячейках D61 и D62 соответственно. В них реализованы следующие формулы: = НОРМСТОБР ((0,9973+1)/2)*D60; = СТЬЮДРАСПОБР (1-0,9973; 47)*D60. Выборка считается репрезентативной, если величина ее относительной ошибки составляет не более 5%, т.е.
Учитывая, что
Рисунок 10
Указанное преобразование возможно в силу того, что величина средней ошибки является одинаковой для Известно, что распределение Стьюдента при увеличении объема выборки стремится к нормальному, а доверительный интервал, вычисленный с его применением является более надежным. Поэтому с точки зрения статистика (исполнителя) целесообразно использовать распределение Стьюдента в малых и больших выборках. Учитывая изложенное, генеральная средняя активов банков с доверительной вероятностью 0,9973 лежит в пределах В практике наиболее часто используется доверительная вероятность равная 0,95 [10], а величина относительной ошибки предельной выборки задается на уровне 5%. Для рассматриваемого примера покажем зависимость объема бесповторной выборки от величины относительной ошибки, начиная с 0,01 до 0,05 с шагом 0,01, и коэффициентов доверия Гаусса от 1 до 3 с шагом 0,5. Объем выборки в случае использования нормального распределения можно вычислить по формуле:
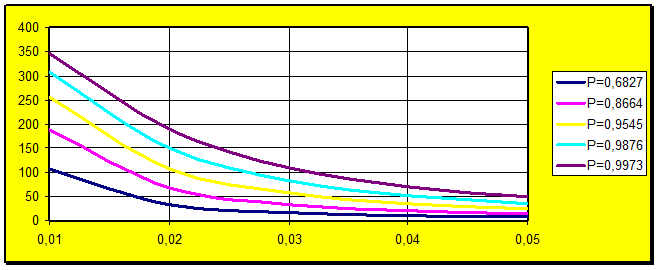
где где фигурные скобки означают округление вверх до ближайшего целого. Формула объема выборки с использованием распределения Стьюдента аналогична приведенной выше, но вместе с тем решение можно получить только применением итерационных методов, так как На рис. 11, 12 показана зависимость объема бесповторной выборки от перечисленных ранее факторов. Анализ рисунков позволяет сделать вывод о том, что выбор величины коэффициентов доверия (вероятностей) и относительной ошибки должен быть достаточно обоснованным, т.к. это приводит к резкому увеличению объема выборки и, как следствие, к возрастанию материальных и временных затрат. Рисунок 11
Рисунок 12
При известных значениях объемов выборок для различных сочетаний
Рисунок 13
Как следует из графика – с увеличением значения относительной ошибки выборки погрешность ее вычисления резко возрастает и превосходит величину относительной ошибки почти в 2 раза. Изломы на графике объясняются дискретностью значений выборки. . 4. АНАЛИЗ ЗАВИСИМОСТИ ПРИБЫЛИ БАНКОВ ОТ СТОИМОСТИ ИХ АКТИВОВ
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , (31)
, (31) (32)
(32)
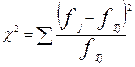 (33)
(33) - эмпирические и теоретические частоты.
- эмпирические и теоретические частоты.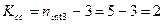 , по которой вычисляется количество степеней свободы.
, по которой вычисляется количество степеней свободы. . Искомая вероятность
. Искомая вероятность  , следовательно эмпирическое распределение не противоречит нормальному.
, следовательно эмпирическое распределение не противоречит нормальному.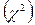 -критерия в критическую область, т.е. проверяется выполнение условия
-критерия в критическую область, т.е. проверяется выполнение условия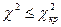 . (34)
. (34)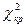 задается уровень значимости и количество степеней свободы. Формула = ХИ2ОБР(0,05; 2) рассчитывает значение 5,99, задающее правостороннюю критическую область (5,99; +∞). Так как условие (34) выполняется, то отклонения теоретических частот от эмпирических являются случайными и распределение активов банков не противоречит нормальному.
задается уровень значимости и количество степеней свободы. Формула = ХИ2ОБР(0,05; 2) рассчитывает значение 5,99, задающее правостороннюю критическую область (5,99; +∞). Так как условие (34) выполняется, то отклонения теоретических частот от эмпирических являются случайными и распределение активов банков не противоречит нормальному.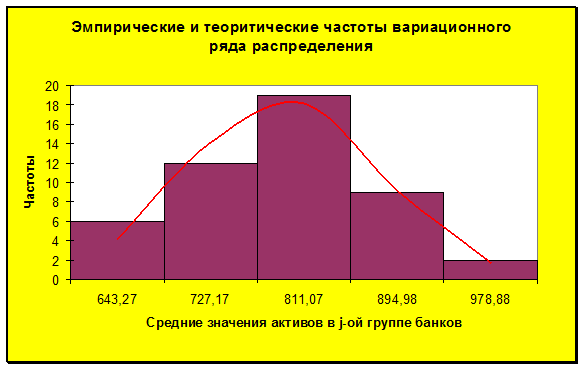
 (35)
(35)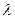 )
)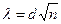 (36)
(36)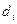 приведены в ячейках AI3: AI7. Следовательно, d=0,036. В ячейке В106 записана формула (36). По известному значению
приведены в ячейках AI3: AI7. Следовательно, d=0,036. В ячейке В106 записана формула (36). По известному значению 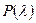 (П.2 табл. 1), если она близка к 1, то расхождение между
(П.2 табл. 1), если она близка к 1, то расхождение между 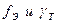 случайны.
случайны.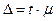 , (37)
, (37)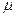 - средняя ошибка выборки.
- средняя ошибка выборки. , (38)
, (38)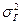 - дисперсия генеральной совокупности;
- дисперсия генеральной совокупности;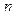 - объем выборочной совокупности;
- объем выборочной совокупности;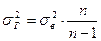 , (39)
, (39)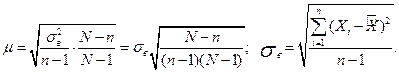 (40)
(40)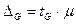
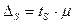
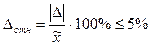 (41)
(41)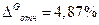 , выборку следует признать представительной. Вместе с тем
, выборку следует признать представительной. Вместе с тем 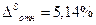 и вывод следует противоположный. В связи с этим, возникает естественный вопрос: какой же из результатов следует считать правильным? В различных источниках существуют разные рекомендации какую выборку считать малой: в одних менее 20 [4], в других менее 30 [5], в третьих менее 40 [10] и т.д. Для ответа на данный вопрос построим график функции
и вывод следует противоположный. В связи с этим, возникает естественный вопрос: какой же из результатов следует считать правильным? В различных источниках существуют разные рекомендации какую выборку считать малой: в одних менее 20 [4], в других менее 30 [5], в третьих менее 40 [10] и т.д. Для ответа на данный вопрос построим график функции , приведенной на рис. 13.
, приведенной на рис. 13.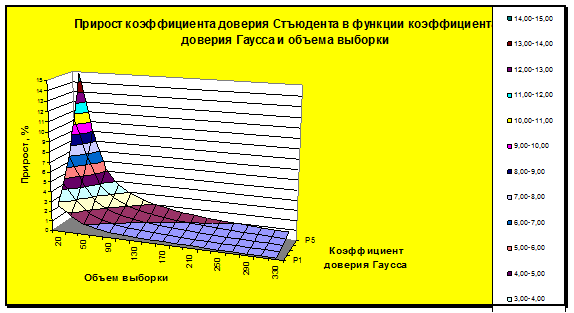
 и
и 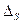 .Коэффициент доверия Гаусса на указанном рисунке изменяется от 1 до 3 с шагом 0,5. Соответствующие ему вероятности имеют следующие значения: 0,6827; 0,8664; 0,9545; 0,9876; 0,9973. Как следует из графика, погрешность в определении предельной ошибки при t =2, n=190 составляет около 1%, что соизмеримо с величиной относительной ошибки предельной выборки.
.Коэффициент доверия Гаусса на указанном рисунке изменяется от 1 до 3 с шагом 0,5. Соответствующие ему вероятности имеют следующие значения: 0,6827; 0,8664; 0,9545; 0,9876; 0,9973. Как следует из графика, погрешность в определении предельной ошибки при t =2, n=190 составляет около 1%, что соизмеримо с величиной относительной ошибки предельной выборки.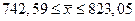 (ячейки D63, D 64).
(ячейки D63, D 64). ,
,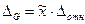 или
или 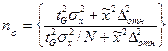 ,
, . Поэтому решения, полученные с применением
. Поэтому решения, полученные с применением 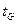 , можно использовать в качестве нулевого приближения для вычисления объемов бесповторной выборки с коэффициентами доверия Стьюдента.
, можно использовать в качестве нулевого приближения для вычисления объемов бесповторной выборки с коэффициентами доверия Стьюдента.
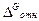 и
и 



