Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел «Общая теория статистики»Содержание книги
Поиск на нашем сайте
Вариант № __
Выполнил: студент __ курса __ группы Сроки сдачи: Иванов В.В. плановый: ________ фактический: _________ Проверил: Петров П.П. Москва – 2006
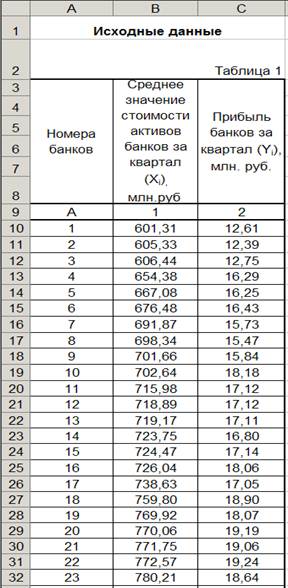
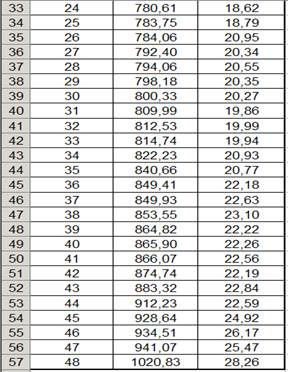
Исходные данные приведены в табл. 1
ПРОВЕРКА ПЕРВИЧНОЙ ИНФОРМАЦИИ НА ОДНОРОДНОСТЬ, НАЛИЧИЕ АНОМАЛЬНЫХ НАБЛЮДЕНИЙ И НОРМАЛЬНОСТЬ РАСПРЕДЕЛЕНИЯ Совокупность считается однородной, если коэффициент ее вариации меньше 33%.
где
n – объем совокупности. Среднее значение вычисляется с помощью функции СРЗНАЧ. Ячейка В60 табл. 2 содержит формулу = СРЗНАЧ (В10:В57), по которой рассчитывается среднее значение активов банков (
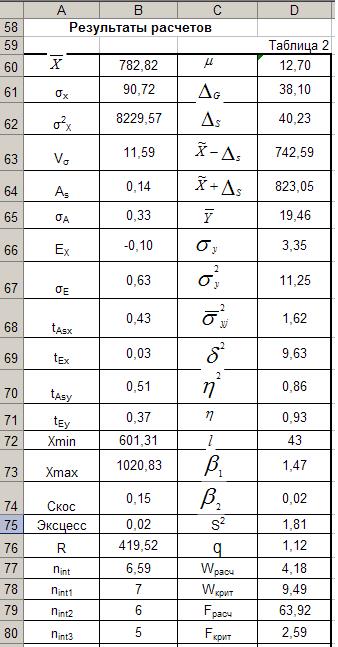
Среднее квадратическое отклонение рассчитывается в предположении, что данные представляют всю генеральную совокупность. В ячейку В61 записана формула СТАНДОТКЛОНП (В10:В57), В ячейку В63 записана формула (1), т.е. = В61/В60*100. Коэффициент вариации равен 11,59%. Если исходные данные являются эмпирическими, то их необходимо проверить на наличие аномальных наблюдений (резко выделяющихся единиц совокупности):
или
Если условия (4) или (5) не выполняются, то соответствующие единицы совокупности исключаются из дальнейшего рассмотрения, а значения Минимальное и максимальное значения совокупности находятся в ячейках В72 и В73. Из приведенных данных следует, что условие (4) выполняется. Гипотеза о нормальном распределении активов банков принимается, если выполняются оба соотношения:
где
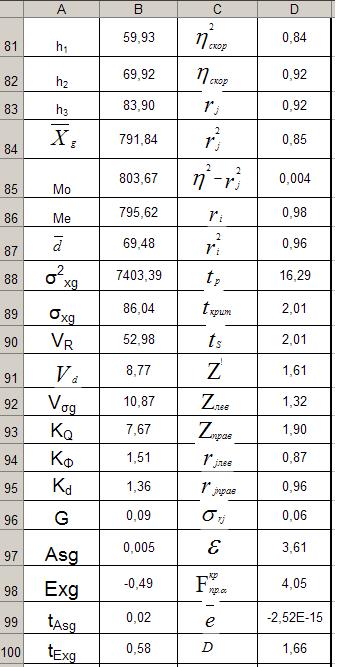
Для вычисления показателя асимметрии в ячейку В64 записана формула (8) = СУММПРОИЗВ((В10:В57-$В$60)^3) /($В$61^3*$A$57). Формула для вычисления эксцесса аналогична предыдущей и отличается показателем степени и наличием вычитаемого числа равного 3. Она реализована в ячейке В66=СУММПРОИЗВ((В10:В57-$В$60)^4)/($В$61^4*$A$57)-3. Учитывая, что оба относительных показателя ( В EXCEL для вычисления показателей асимметрии и эксцесса существуют функции СКОС и ЭКСЦЕСС. В них реализованы приближенные формулы для вычисления перечисленных показателей выборочных совокупностей. Использовать их нецелесообразно в связи с тем, что ранее было принято допущение, что исходная совокупность является генеральной. Анализ результатов расчета позволяет сделать следующие выводы: 1) Совокупность активов банков однородна ( 2) Аномальные наблюдения отсутствуют. 3) Распределение активов банков плосковершинно и имеет правостороннюю асимметрию. Отклонения эмпирических частот от теоретических носят случайный характер, следовательно эмпирическое распределение активов банков не противоречит нормальному. ВАРИАЦИОННЫЙ РЯД РАСПРЕДЕЛЕНИЯ АКТИВОВ БАНКОВ И СИСТЕМА ПОКАЗАТЕЛЕЙ ВЫЧИСЛЯЕМАЯ НА ЕГО ОСНОВЕ Определение количества групп Количество групп (интервалов) вариационного ряда вычислим по формуле Стерджесса:
Из практики известно, что выражение (13) дает удовлетворительные результаты при n>100. Кроме того, чтобы рассчитать среднее значение прибыли в j-ой группе банков, их количество (частота) должно быть не менее двух. Учитывая изложенное выполним расчет для 7, 6 и 5 интервалов. В ячейку В78 запишем формулу = ОКРВВЕРХ (В77, 1), а в В79 = ОКРВНИЗ (В77,1). Содержимое ячейки В80 определяется выражением = В79-1. Ширина интервала рассчитывается по формуле:
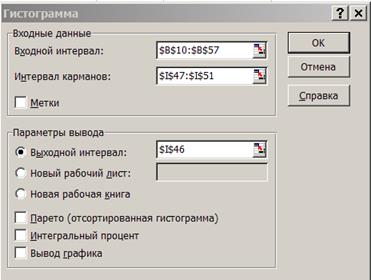
где Для определения количества банков, попадающих в j-ую группу воспользуемся режимом «Гистограмма». В диалоговом окне данного режима (рис. 1) задаются следующие параметры: Рисунок 1
1. Входной интервал- вводится ссылка на ячейки, содержащие анализируемые данные. 2. Интервал карманов (необязательный параметр) – вводится ссылка на ячейки, содержащие набор граничных значений, определяющих интервалы (карманы). Эти значения должны быть введены в возрастающем порядке. В Excel вычисляется число попаданий данных (частоты) в сформированные интервалы. Границы интервалов являются строгими нижними и нестрогими верхними: 3. Метки - флажок устанавливается в активное состояние, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок следует дезактивировать. В этом случае автоматически будут созданы стандартные названия для данных входного диапазона. 4. Выходной интервал/ Новый рабочий лист/ Новая рабочая книга. Переключатель в положении Выходной интервал активизирует поле, в которое необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экране появится сообщение в случае возможного наложения выходного диапазона на исходные данные. В положении Новый рабочий лист открывается новый лист, в который начиная с ячейки А1 вставляются результаты анализа. Если необходимо задать имя открываемого листа, введите его в поле напротив соответствующего положения переключателя. В положении Новая рабочая книга открывается новая книга, на первом месте которой, начиная с ячейки А1 вставляются результаты анализа. 5. Парето (отсортированная диаграмма) – устанавливается в активное состояние, чтобы представить данные в порядке убывания частоты. Если флажок снят, то данные в выходном диапазоне будут приведены в порядке следования интервалов. 6. Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных частот и включения в диаграмму графика кумуляты. 7. Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон. Воспользуемся тем обстоятельством, что интервалы карманов задавать необязательно и построим соответствующую диаграмму (рис. 2).
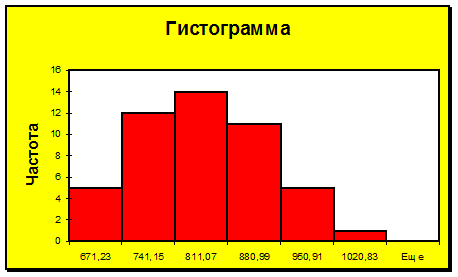
Рисунок 2
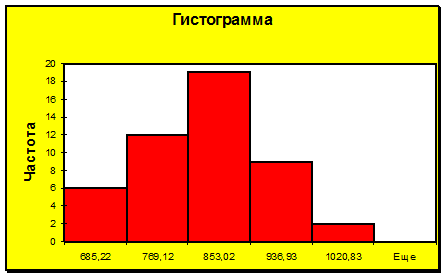
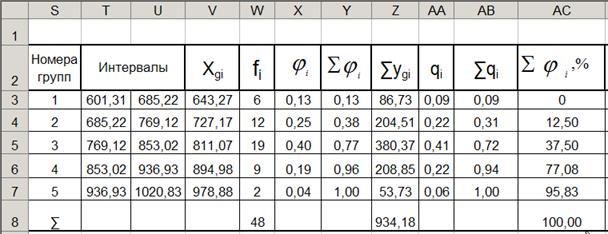
Как следует из табл. 3 и диаграммы в первой и седьмой группах частота равна 1. Следовательно данный вариант является неприемлемым. Изложенное справедливо и для диаграмм, приведенных на рис. 3, 4.
Рисунок 4
Следовательно, за основу необходимо принять вариант, содержащий 5 групп банков (табл. 6 рис. 6). Диалоговое окно режима «Гистограмма» для построения диаграммы с 5-ю интервалами приведено на рис. 5.
Рисунок 5
Рисунок 6
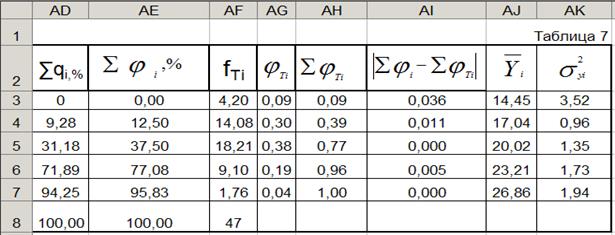
Для выполнения дальнейших расчетов, полученные результаты (интервалы и частоты) перепишем в табл. 7.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

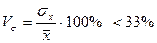 , (1)
, (1)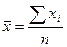 - среднее значение; (2)
- среднее значение; (2)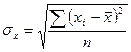 - среднее квадратическое отклонение; (3)
- среднее квадратическое отклонение; (3)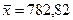 )
)
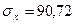 .
.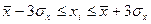 (4)
(4)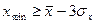 , (5)
, (5)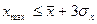 .
.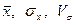 пересчитываются.
пересчитываются.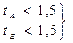 , (6)
, (6)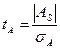 - относительный показатель ассиметрии; (7)
- относительный показатель ассиметрии; (7)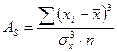 - показатель ассиметрии; (8)
- показатель ассиметрии; (8)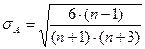 - средняя квадратическая ошибка асимметрии; (9)
- средняя квадратическая ошибка асимметрии; (9)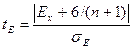 - относительный показатель эксцесса; (10)
- относительный показатель эксцесса; (10)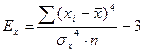 - показатель эксцесса; (11)
- показатель эксцесса; (11)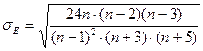 - средняя квадратическая ошибка эксцесса. (12)
- средняя квадратическая ошибка эксцесса. (12)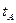 и
и 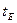 ) меньше 1,5, гипотезу о нормальном распределении активов банков следует принять.
) меньше 1,5, гипотезу о нормальном распределении активов банков следует принять.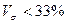 ), следовательно, средняя величина является обобщающей характеристикой активов банков и отражает типичный уровень в расчете на один банк в конкретных условиях места и времени.
), следовательно, средняя величина является обобщающей характеристикой активов банков и отражает типичный уровень в расчете на один банк в конкретных условиях места и времени.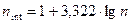 . (13)
. (13)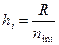 , (14)
, (14)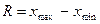 - размах вариации (15)
- размах вариации (15)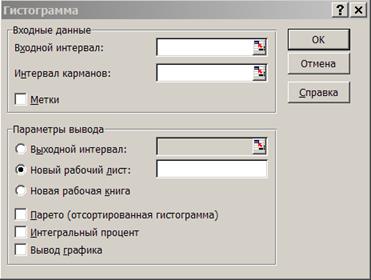
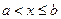 . Поэтому целесообразно задавать только верхние границы интервалов. Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
. Поэтому целесообразно задавать только верхние границы интервалов. Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.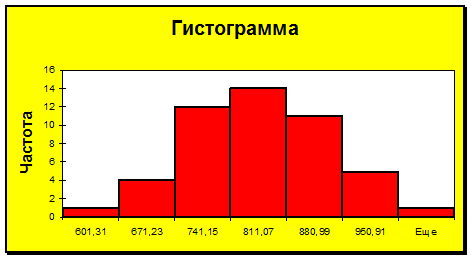
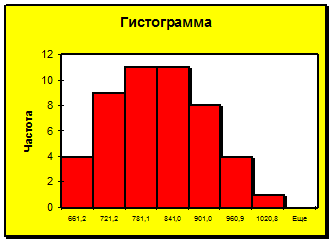 Рисунок 3
Рисунок 3