
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача про статистичну перевірку гіпотези і критерій узгодження.Содержание книги
Поиск на нашем сайте Статистичною називають гіпотезу про вигляд розподілу генеральної сукупності або про параметри відомих уже розподілів. Статистичні гіпотези поділяються на дві основні групи: · непараметричні гіпотези — це гіпотези про закони розподілу ймовірностей випадкової величини генеральної сукупності; · параметричні гіпотези — це гіпотези про значення параметрів законів розподілу ймовірностей випадкової величини генеральної сукупності. Сформульована гіпотеза, яка піддається перевірці, називається нульовою(основною). Гіпотеза, яка єсуперечить нільовій чи є протилежною до не називається альтернативною (конкуруючою). Оскільки перевірка основної гіпотези проводиться за даними вибірки статистичними методами, то цю перевірку називають статистичною. Імовірність допустити помилку першого роду називається рівнем значущості. Статистичним критерієм гіпотези (або просто критерієм) називають випадкову величину К, за допомогою якої перевіряється основна гіпотеза. Значення випадкової величини К, яке обчислене на основі певної вибірки, називається емпіричним (або спостережним) значення критерію гіпотези. Множина значень критерію К, за яких основна гіпотеза відхиляється, називається критичною областю (КО). Множина значень критерію К, за яких основна гіпотеза приймається, називається областю прийняття гіпотез (ОПГ). Критерій узгодження Пірсона (критерій)для перевірки гіпотези про закон розподілу генеральної сукупності. Критерії, які призначені для перевірки сформульованих гіпотез, називаються критеріями узгодження. Згідно з критерієм Пірсона для перевірки гіпотези вводиться випадкова величина К:
Де m- число варіант(чи інтервалів);
Перевірка гіпотез про вигляд математичного сподівання нормально розподіленої випадкової величини у випадку коли дисперсія відома. Коли дисперсія генеральної сукупності Дr(Х) відома. Допускається, що відомі п,а1,а. Правило 1. Якщо Н0:а = а0, а Н1: а 1. Обчислюється хв. 2. Обчислюється емпіричне значення критерію за формулою
3.За таблицею значень інтегральної функції Лапласа знаходять критичну точку kkp двосторонньої критичної області з рівності
3. Робиться висновок:
Правило 2. Якщо Н0:а = а0, а H1: а > а0, то перевірка гіпотези здійснюється подібно до правила 1 із змінами: 1. Визначають критичну точку kп.кр правосторонньої критичної області, користуючись при цьому) рівністю
2. Робиться висновок: · · Правило 3. Якщо Н0:а = а0, а II, \ а < а0, то перевірка гіпотези здійснюється подібно до попереднього правила 2 із змінами у висновку, ураховуючи, що критична точка лівостороння, тобто що кл кр - -кпІкр:
Перевірка гіпотез про вигляд математичного сподівання нормально розподіленої випадкової величини у випадку коли дисперсія невідома. Дисперсія генеральної сукупності невідома. Допускається, що відомі п, а0, а. Правило 1. Якщо Н0: а = а0, а Н1: а 1. Обчислюється хв. 2. Обчислюється виправлена вибіркова дисперсія Dв. 3. Обчислюється емпіричне значення критерію Стьюдента за формулою
4. За таблицею критичних точок Стьюдента за даними 5. Робиться висновок:
Правило 2. Якщо Н0: а = а0, а Н1: а > а, то перевірка гіпотези здійснюється подібно до правила 1 для цього випадку з певними змінами: 6. За таблицею критичних точок Стьюдента за даними 7. Робиться висновок:
Правило 3. Якщо Н0:а = а0, Н1: а < а0, то перевірка гіпотези здійснюється подібно до попереднього правила 2 із змінами у висновку, враховуючи, що критична точка -лівостороння, тобто що
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.94 (0.008 с.) |

 ,
, - спостережувана частота
- спостережувана частота - теоретична частота
- теоретична частота - імовірність того, що значення випадкової величини Х належить до і-тої групи.
- імовірність того, що значення випадкової величини Х належить до і-тої групи.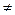 а0, то перевірка гіпотези здійснюється за правилом:
а0, то перевірка гіпотези здійснюється за правилом:





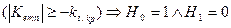

 , зосередженому у верхньому рядку таблиці, і числом ступенів вільності к = п-1 знаходять критичну точку
, зосередженому у верхньому рядку таблиці, і числом ступенів вільності к = п-1 знаходять критичну точку  двосторонньої критичної області.
двосторонньої критичної області.






