
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення відносної частоти події і статистичної ймовірності. Спільність і різниця між класичною ймовірністю і відносною частотою події.Содержание книги
Поиск на нашем сайте Відносна частота події А називається числа експериментів, у яких подія А відбулась, до числа усіх експериментів: Статистичною ймовірністю події А називається число Р(Ф), навколо якого коливається відносна частота появи цієї події в довгих серіях експериментів.
Геометричне визначення ймовірності та її обчислення. Геометричним означенням користуються коли число наслідків нескінченне, але наслідки рівно можливі. Наприклад, точку, кидаємо в область G і треба оцінити можливість попасти в область g. Отже, імовірність події А називається відношення міри g до G, тобто P (A)= mes g/mes G Mes – міра область(довжина,площа_ g – частина області G
Поняття сумісних і несумісних подій. Як обчислити ймовірність суми несумісних подій. Дві події А і В називають несумісними коли їх добуток є неможлива подія. Несумісність подій А і означає, що поява події А виключає можливість появи події В і навпаки. Сумісними подіями називають такі події, що поява однієї не виключає можливості появи іншої. Ймовірність суми несумісних подій: р (А+В)=Р(А)+Р(В)
Повна група подій. Ймовірність протилежної події. Події А1, А2,……..Аи утворюють повну групу, якщо в результаті виконання експкрименту принаймні одна з цих подій обов’язково відбудеться. Протилежною подією до події а називається подія, що складається з усіх елементів які не входять до події А. Отже,подія протилежна відбудеться тоді і тільки тоді, коли не відбудеться п.А.
Умовна ймовірність події. Імовірність добутку залежних і незалежних подій. Умовною ймовірністю події А за умови що подія В відбудеться називають відношення: Р(А/В)=Р(АΩВ)/Р(В). Імовірність добутку залежних і незалежних подій. Для залежних: імовірність появи двох випадкових подій довірнює добутку ймовірності однієї з них та умовної ймовірності другої за умови,що відбулась перша. Для незалежних: імовірність появи двох незалежних подій дорівнює добутку їх ймовірностей.
Імовірність суми сумісних подій. Імовірність появи хоча б однієї з декількох подій. Сумою 2-х сумісних подій називають подію, що складається з появи або події A, або події B, або обох їх одразу (одночасно). Імовірність появи хоча б однієї з двох сумісних подій дорівнює сумі імовірностей цих подій без імовірності їх спільної появи:
Формула повної ймовірності. Якщо Н1, Н2, ……,Ни – повна група попарно несумісних подій і Р(Ні) >0, і=1,2….и, то для будь якої п.А справедлива рівність: Р(А) = Формула виражає ймовірність п.А за умови, що відбулась одна і тільки одна з попарно несумісних подій Н1, Н2, ……,Ни.
Імовірність гіпотез і формули Байєса. Нехай набір подій Н1, Н2, ……,Ни утворює повну групу попарно несумісних подій. Тоді для будь якої випадкової події А виконується рівності Р(Ні/А)=Р(Ні)Р(А/Ні): Імовірність гіпотез Ні(І= 1,2…и) вказується якою саме умовою відбудеться п. А Щоб визначити ймовірність того, що подія А відбулась і наскільки їй при цьому сприяла гіпотеза Ні, тобто визначити Р(Ні), користуються ф-лою Баєса.
Послідовність незалежних випробувань за схемою Бернуллі та умови застосування. Випробування називаються незалежними стосовно деякої події А, якщо ймовірність цієї події в кожному випробуванні не залежить від результатів інших випробувань. Серія повторних незалежних випробуванньз одним із можливих результатів а і неА у кодному з яких подя а має одну і ту ж імовірність появи Р (А)=р, називається схемою Бернуллі. Імовірність Ри(М) тго, що в результаті и незалежних випробуваннь подія А зявиться рівно м разів (М=0,1,2,…и), обчислюється за формулою
Локальна теорема Лапласа та умови застосування. Якщо у схемі Бернуллі кількість незалежних випробувань є велика,то ймовірність появи події А м разів наближено знаходимо за формулою:
Інтегральна теорема Лапласа. Якщо у схемі Бернуллі и є досить великим, то ймовірність появи події А не менша ніж м1 і не більша ніж м2 разів наближено може бути знайдена за формулою:
Формула Пуассона для обчислення ймовірностей в схемі незалежних випробувань Бернуллі та умови застосування.
Формула Пуассона. Якщо в кожному з n незалежних повторних випробувань, а n велике, то
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |


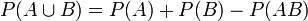



 , де
, де 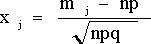 ,
,  , а
, а  .
.



