
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы) Корреляционно-регрессионный анализСодержание книги
Поиск на нашем сайте Важнейшей задачей является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи (уравнения регрессии). Могут иметь место различные формы связи: прямолинейная
криволинейная в виде: параболы второго порядка (или высших порядков)
гиперболы
показательной функции
Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):
Если связь выражена параболой второго порядка (
Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения
Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости. Непараметрические методы Методы непосредственной оценки и проверки гипотез о теоретическом распределении вероятностей и тех или иных его общих свойствах (симметрии, независимости и т. п.) по результатам наблюдений. Название "Непараметрические методы" подчёркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений), и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Особенность непараметрических методов в отличие от классических методов состоит в независимости от неизвестного теоретического распределения. Преимущества непараметрических методов: 1.Могут использоваться для проверки гипотез о параметрах генеральной совокупности, когда переменная Не распределена нормально. 2.Могут использоваться для номинальных и порядковых данных. 3.Могут использоваться для проверки гипотез, которые не связаны с параметрами генеральной совокупности. 4В большинстве случаев для непараметрических методов вычисления проще, чем для параметрических. Методы более понятны.
Недостатки непараметрических методов:
1. Они менее точны, чем соответствующие параметрические критерии. 2. Они менее информативны. 3. Они менее эффективны. Например, для критерия знаков нужна выборка из 100 человек, в то время, как для получения аналогичных результатов при использовании z - критерия достаточно было бы выборки из 60 человек.
Расчет перспективы численности населения. Общий прирост численности населения страны за год складывается как в результате его естественного движения, так и в результате механического (миграционного) перемещения отдельных лиц. Для его характеристики в статистике применяется коэффициент общего прироста населения: К общ.пр = Кр – Ксм + Кобщ.миг. Одной из задач статистики населения является определение численности населения на перспективу. Простейший прием расчета перспективной численности населения (всего) основывается на использовании данных об общем приросте населения (естественном и механическом) за определенный анализируемый период и предположение о сохранении выявленной закономерности на прогнозируемый отрезок времени. Перспективная численность населения через t лет:
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |






 )
)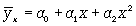 ), то систему нормальных уравнений для отыскания параметров a0, a1, a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде
), то систему нормальных уравнений для отыскания параметров a0, a1, a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде
 :
:
 - дисперсия в ряду фактических значений у.
- дисперсия в ряду фактических значений у.





