
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы передачи управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте К операторам передачи управления относят оператор безусловного перехода, иначе – оператор безусловной передачи управления (goto), оператор возврата из функции (return), оператор выхода из цикла или переключателя (break) и оператор перехода к следующей итерации цикла (continue). Оператор безусловного перехода имеет вид goto идентификатор; где идентификатор – имя метки оператора, расположенного в той же функции, где используется оператор безусловного перехода. Передача управления разрешена на любой помеченный оператор в теле функции. Однако существует одно важное ограничение: запрещено «перескакивать» через описания, содержащие инициализацию объектов. Это ограничение не распространяется на вложенные блоки, которые можно обходить целиком. Следующий фрагмент иллюстрирует сказанное: … goto B;/*Ошибка. Попытка «перескочить» через определение*/ float z = 0.0; // переменной z. goto B; /*Ошибки нет. Определение переменной n находится внутри блока*/ { int n = 10; z = n*z+z; } B: cout<<”\n x = “<<x; /*Строка, на которую передаётся управление.*/ Все операторы блока достижимы для перехода к ним из внешних блоков. Однако при таких переходах необходимо соблюдать то же самое правило: нельзя передавать управление в блок, обходя инициализацию. Следовательно, будет ошибочным переход к операторам блока, перед которыми помещены определения с явной или неявной инициализацией. Это же требование обязательного выполнения инициализации справедливо и при внутренних переходах в блоке. Следующий фрагмент содержит обе указанные ошибки: {… //Внешний блок goto ABC; // Во внутренний блок, минуя описание ii { int ii = 15; //Внутрений блок … ABC: … goto XYZ; //Обход описания СС char CC = ‘ ‘; … XYZ: … } … } В принятом в настоящее время стиле программирования принято либо вовсе отказаться от оператора goto, либо свести его применение к минимуму и строго придерживаться следующих рекомендаций: не входить внутрь блока извне; не входить внутрь условного оператора, т.е. не передавать управление операторам, размещённым после служебных слов if или else; не входить извне внутрь переключателя (switch); не передавать управление внутрь цикла. Следование перечисленным рекомендациям позволяет исключить возможные нежелательные последствия бессистемного использования оператора безусловного перехода. Полностью отказываться от оператора goto вряд ли стоит. Есть случаи, когда этот оператор обеспечивает наиболее простые и понятные решения. Оператор возврата из функции имеет вид return выражение; или просто return; Выражение, если оно присутствует, может быть только скалярным. Например, следующая функция вычисляет и возвращает квадрат значения своего аргумента: float square(float z){return z*z;} Выражение в операторе return не может присутствовать в том случае, если возвращаемое функцией значение имеет тип void. Например, следующая функция выводит на экран дисплея значение третьей степени своего аргумента и не возвращает в точку вызова никакого значения: void cube_print(float z){ cout «"\t cube = " «z * z * z; return; } В данном примере оператор возврата из функции не содержит выражения. Оператор break служит для принудительного выхода из цикла или переключателя. Определение "принудительный" подчеркивает безусловность перехода. Например, в случае цикла не проверяются и не учитываются условия дальнейшего продолжения итераций. Оператор break прекращает выполнение оператора цикла или переключателя и осуществляет передачу управления (переход) к следующему за циклом или переключателем оператору. При этом, в отличие от перехода с помощью goto, оператор, к которому выполняется передача управления, не должен быть помечен. Оператор break нельзя использовать нигде, кроме циклов и переключателей. Необходимость в использовании оператора break в теле цикла возникает, когда условия продолжения итераций нужно проверять не в начале итерации (циклы for, while), не в конце итерации (цикл do), а в середине тела цикла. В этом случае тело цикла может иметь такую структуру: { операторы if (условие) break; операторы } Например, если начальные значения целых переменных i, j таковы, что i < j, то следующий цикл определяет наименьшее целое, не меньшее их среднего арифметического: while(i<j){ i++; if (i == j) break; j--; } Оператор break практически незаменим в переключателях, когда с их помощью надо организовать разветвление. Например, следующая программа печатает название любой, но только одной, восьмеричной цифры: //Программа 4.4 #include "stdafx.h" #include <iostream> void main(){ int ic; std::cout<<"\n Input octuple number: "; std::cin>>ic; std::cout << "\n" << ic; switch(ic){ case 0: std::cout << " - zero"; break; case 1: std::cout << " - one"; break; case 2: std::cout << " - two"; break; case 3: std::cout << " - three"; break; case 4: std::cout << " - four"; break; case 5: std::cout << " - five"; break; case 6: std::cout << " - six"; break; case 7: std::cout << " - seven"; break; default: std::cout << " - this is not octuple number!"; } getchar(); } Программа напечатает название только одной введенной цифры и прекратит работу. Если в ней удалить операторы break, то в переключателе будут последовательно выполнены все операторы, начиная с помеченного нужным (введенным) значением. Циклы и переключатели могут быть многократно вложенными. Однако следует помнить, что оператор break позволяет выйти только из самого внутреннего цикла или переключателя. Например, в следующей программе, которая в символьном массиве подсчитывает количество нулей (ko) и единиц (kl), в цикл вложен переключатель: //Программа 4.5 #include "stdafx.h" #include <iostream> void main(void){ char c[] = "ABC100111"; int k0 = 0, kl = 0; for (int i = 0; c[i]!= '\0'; i++) switch (c[i]){ case '0': k0++; break; case '1': kl++; break; default: break; } std::cout<< "\n In string " <<k0 << " zero, " <<kl << " units "; getchar(); } Результат выполнения программы: В строке 2 нуля, 4 единицы Оператор break в данном примере передает управление из переключателя, но не за пределы цикла. Цикл продолжается до естественного завершения. При многократном вложении циклов и переключателей оператор break не может вызвать передачу управления из самого внутреннего уровня непосредственно на самый внешний. Поэтому удобнее всего для этого пользоваться не оператором break, а оператором безусловной передачи управления (goto). Оператор continue употребляется только в операторах цикла. С его помощью завершается текущая итерация и начинается проверка условия дальнейшего продолжения цикла, т.е. условий начала следующей итерации. Типичный пример использования оператора continue: подсчитать среднее значение только положительных элементов одномерного массива: for (s=0.0, k=0, i = 0; i<n; i++) { if(x[i] <= 0.0) continue; k++; //-Количество положительных элементов в массиве s += x[i]; // Сумма положительных элементов массива } if (k > 0) s = s/k; // Среднее значение Выполнение оператора continue эквивалентно окончанию текущей итерации цикла и началу проверки для принятия решения о начале новой итерации.
Примеры численного моделирования цепей первого порядка Из курса математики известно, что интеграл - это есть площадь, заключённая между графиком функции и осью абсис, т.е. для того чтобы найти значение определённого интеграл функции
где h = (b-a)/N; N –произвольное целое число. Понятно, что чем больше N, тем меньше шаг h и тем точнее результат численного интегрирования.
Рис. 4.8. Пояснения к методам численного интегрированния: а) точное значение интеграла b) вычисление значениея интеграла методом прямоугольников; с) вычисление значениея интеграла методом трапеций
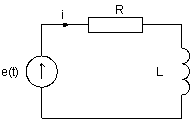
Методы численного интегрирования широко применяются при моделировании цепей и сигналов. Приведём два простейших примера. Найдём выражения для численного расчёта токов и напряжения на реактивных элементах в цепях, изображённых на рис. 4.9. Будем считать, что в момент времени t = 0 значение независимого источника напряжения e(t0) изменилось с 0 до 1 В (единичный скачёк), R =10кОм, C = 10 мкФ, L = 10мкГ.
Рис. 4.9. Моделируемая RС и RL цепь
Как известно, токи и напряжения на ёмкости C и индуктивности L связанны соотношениями:
Проинтегрировав оба уравнения, получим
Применяя метод трапеции к левым частям равенств и находя интеграл в правых частях, получим итерационные выражения:
где h – шаг численного интегрирования. Выражая напряжение через ток, получим для ёмкости С и индуктивности L итерационные выражения:
Запишем уравнения, описывающие зависимость токов и напряжений в RC и RL цепях (первый закон Киргоффа, закон коммутации, компонентные уравнения элементов цепи)
Подставив в первый закон Киргоффа вместо uC и uL полученные выше итерационные выражения, запишем:
Выберем значение шага интегрирования h = 0.1RC = 0.1мc как одну десятую от постоянной времени цепи. Исходя из законов коммутации, определим значение токов и напряжений на реактивных элементах в момент коммутации (t = t0 = 0).
Подставим численные значения в выражения и найдём значение тока i(t1) в RC и RL цепи.
Далее находим из выражения (4.1, 4.2) значение uC(t1) и uL(t1), подставляем их в выражение (4.3, 4.4) вместо uC(t0) и uL(t0), а вместо i(t0), естественно, i(t1), и находим i(t2) и т.д. Программа, реализующая расчёт напряжения и тока на ёмкости С RC-цепи, приведённой на рис. 4.9, представлена ниже. Она расчитывает первые сорок значений напряжения и тока на ёмкости C. Графики напряжения и тока на С при R =10кОм, C = 10 мкФ, Е = 1В приведены на рис 4.10. //Программа 4.6 #include "stdafx.h" #include <iostream> void main(){ double R, C, E, t = 0; std::cout<<"\nInput R = ";std::cin>>R; std::cout<<"\n Input C = ";std::cin>>C; std::cout<<"\n Input a size jump E = ";std::cin>>E; double Uc0 = 0, Ic0 = E/R, h = 0.1*R*C; double Uc1, Ic1; std::cout<<"\n t = "<<t<<" E = "<<E<<" Uc1 = "<<Uc0<<" Ic1 = "<<Ic0; for(int i = 0; i < 40; i++){ Ic1 = (E - Uc0 - h/(2*C)*Ic0)/(R + h/(2*C)); Uc1 = h/(2*C)*Ic1 + Uc0 + h/(2*C)*Ic0; t = t+h; std::cout<<"\nt="<<t<<"E="<<E<<"Uc1="<<Uc1<<"Ic1="<<Ic1; Uc0 = Uc1; Ic0 = Ic1; } getchar(); }
Рис. 4.10. Графики напряжение и ток на ёмкости при R =10кОм, C = 10 мкФ, Е = 1В
Написать программу и рассчитать значение тока и напряжения на индуктивности L в RL цепочки по полученным выражениям (4.4) и (4.6) рекомендую студентам самостоятельно.
|
|||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 920; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.013 с.) |

 , необходимо найти площадь S (рис. 4.8). Эту площадь можно найти аналитически, решив интеграл, или численно. Существует различные численные методы интегрирования, но мы рассмотрим только два простейших: метод прямоугольников и метод трапеций. Суть методов поясним с помощью рис. 4.8. Значение интегралла можно приближённо рассчитать, найдя сумму площадей прямоугольнков (рис. 4.8,b) или сумму плащадей трапеций (рис. 4.8,c).
, необходимо найти площадь S (рис. 4.8). Эту площадь можно найти аналитически, решив интеграл, или численно. Существует различные численные методы интегрирования, но мы рассмотрим только два простейших: метод прямоугольников и метод трапеций. Суть методов поясним с помощью рис. 4.8. Значение интегралла можно приближённо рассчитать, найдя сумму площадей прямоугольнков (рис. 4.8,b) или сумму плащадей трапеций (рис. 4.8,c).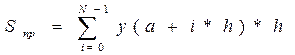
 ,
,


 .
.
 .
. ,
, ,
, , (4.1)
, (4.1) . (4.2)
. (4.2)

 , (4.3)
, (4.3) . (4.4)
. (4.4) (4.5)
(4.5) . (4.6)
. (4.6) ,
, .
.



