
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»Содержание книги
Поиск на нашем сайте
формулу правильно один раз, а затем скопировать в остальные ячейки, при этом, как известно, она «настраивается» на соответствующую ячейку.
Таблица 7.4 Результаты вычислений, выполненных в табличном процессоре
Следует заметить, что для хранения результатов расчетов в данном случае требуется очень много ячеек таблицы, и хотя современные табличные процессоры позволяют хранить большой объем информации, в случае нехватки памяти рекомендуется увеличить шаг, с которым проводятся вычисления (при этом пожертвуем точностью вычислений). Табличный процессор позволяет представлять результаты расчетов и в графической форме. Можно при работе над задачей получить результаты двумя способами: с помощью табличного процессора и составлением собственной программы - для того. чтобы затем сравнить эти результаты и временные затраты каждого из способов. Но, несмотря на успешное применение табличного процессора при решении простейшей учебной задачи, следует признать, что для решения более громоздких в вычислительном плане задач предпочтительнее программировать самим. А теперь ответим на вопрос, поставленный в задаче. Известен такой факт: один из американских каскадеров совершил прыжок в воду с высоты 75 м (Бруклинский мост), и скорость приземления была 33 м/с. Сравнение этой величины с получившейся у нас конечной скоростью 37,76 м/с позволяет считать описанный в кинофильме эпизод вполне возможным. Обсуждаемой модели можно придать черты оптимизационной, поставив задачу так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Или по-другому: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k2), чтобы скорость приземления была безопасной? Выполнение таких исследований многократно более трудоемко, нежели просто изучение одного прыжка при заказанных условиях.
ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ. ЗАКОНЫ ПОДОБИЯ
Рассмотрим эту известную задачу с учетом сопротивления воздуха. Будучи брошенным под углом α к горизонту с начальной скоростью v0, тело летит, если не учитывать сопротивления воздуха, по параболе, и через некоторое время падает на землю. Напомним элементарное решение этой задачи. Разложим скорость на горизонтальную и вертикальную составляющие:
Поскольку движение по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным - после нее; движение же по горизонтали является равномерным. Из формул равноускоренного движения vy = v
Высота этой точки
Полное время движения до падения на землю 2
Для нахождения траектории достаточно из текущих значений x и у исключить t:
следовательно,
Уравнение (7.11) - уравнение параболы. Полученные формулы могут, в частности, послужить для тестирования будущей компьютерной программы. При достаточно большой начальной скорости сопротивление воздуха может значительно изменить характер движения. Прежде чем выписывать уравнения, вновь оценим, какая из составляющих силы сопротивления - линейная или квадратичная по скорости - дает больший вклад в эту силу, и нельзя ли одной из этих составляющих пренебречь. Оценку проведем для шарика; по порядку величины оценка не зависит от формы тела. Итак, шарик радиусом r ≈ 0,1 м, движущийся со скоростью ~ 1 м/с, испытывает в воздухе линейную (стоксову) силу сопротивления
и квадратичную силу сопротивления
Величины F1 и F2 сопоставимые (как принято говорить, «одного порядка», так как они различаются менее, чем в 5 раз). При увеличении размера тела F2 растет быстрее, чем F1 (F1 ~ r, F2 ~ r2), при увеличении скорости F2 также растет быстрее, чем F1 (F1 ~ v, F2 ~ v2). Таким образом, если мы моделируем движение брошенного мяча, камня, то необходимо в уравнениях удерживать обе составляющие силы сопротивления, но если мы захотим моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь. Проецируя уравнение
Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то
где θ - угол между текущим направлением скорости и осью х. Подставляя это в уравнение и учитывая, что
Поскольку представляет несомненный интерес и траектория движения, дополним систему (7.12) еще двумя уравнениями
и, решая их совместно с (7.12), будем получать разом четыре функции: vx(t), vy(t), x(t), y(t). Прежде чем дать пример решения обсуждаемой задачи, покажем очень полезный прием, чрезвычайно популярный в физическом моделировании, называемый обезразмериванием. При решении конкретных задач мы пользуемся определенной системой единиц (СИ), в которой далеко не все числовые значения лежат в удобном диапазоне. Кроме того, абсолютные значения величин дают мало информации для качественного понимания. Скорость 15 м/с - много это или мало? Все дело в том, по сравнению с чем. Именно в сравнении с чем-то привычным и понятным мы обычно и воспринимаем слова «много» и «мало», даже если делаем это бессознательно. Идея обезразмеривания заключается в переходе от абсолютных значений расстояний, скоростей, времен и т.д. к относительным, причем отношения строятся к величинам, типичным для данной ситуации. В рассматриваемой задаче это особенно хорошо просматривается. В самом деле, при отсутствии сопротивления воздуха мы имеем значения l, h, t, определенные выше; сопротивление воздуха изменит характер движения, и если мы введем в качестве переменных величины
- безразмерные расстояния по осям и время, - то при отсутствии сопротивления воздуха эти переменные будут изменячься в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления. Для скоростей естественно ввести безразмерные переменные, соотнося проекции скорости на оси x и у с начальной скоростью v0:
Покажем, как перейти к безразмерным переменным в одном из наших уравнений, например, во втором уравнении системы (7.12). Имеем:
(так как постоянный множитель можно вынести за знак производной). Подставляя это в уравнение, получаем
или
Подставляя
получаем
где безразмерные комбинации параметров, входящих в исходные уравнения,
Выполним обезразмеривание во всех уравнениях (7.12), (7.13) (рекомендуем читателям проделать эту процедуру самостоятельно). В результате получим
Начальные условия для безразмерных переменных таковы:
Важнейшая роль обезразмеривания - установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в уравнения (7.12), (7.13) или являющихся для них начальными условиями: k1, k2, m, g, v0, а. После обезразмеривания переменных появляются безразмерные комбинации параметров - в данном случае a, b, α - фактически определяющие характер движения. Если мы изучаем два разных движения с разными размерными параметрами, но такие, что а, b и α одинаковы, то движения будут качественно одинаковы. Число таких комбинаций обычно меньше числа размерных параметров (в данном случае вдвое), что также создает удобство при полном численном исследовании всевозможных ситуаций, связанных с этим процессом. Наконец, как уже отмечалось, величины Vx, Vy, X, Y, τ физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден. Прежде чем предпринимать численное моделирование, отметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение. Система уравнений (7.14) при b = 0достаточноэлементарно интегрируется и результаты таковы:
Исключая из двух последних формул время, получаем уравнение траектории:
Заметим, что эта формула не из тех, которые привычно визуализируются, например, по сравнению с совершенно отчетливой формулой (7.11), и здесь компьютер может быть полезен в том, чтобы составить ясное представление о влиянии линейной части силы сопротивления на изучаемое движение.
Рис. 7.8. Семейство траекторий при α = 45° и значениях α, равных 0,01; 0,1; 1 и 10 (кривые - справа налево)
На рис. 7.8 приведены траектории четырех движений с разными значениями параметра α, характеризующего трение. Видно, как сильно оно влияет на движение - его форму, расстояния по вертикали и горизонтали. Общее исследование при произвольных значениях а и b поможет выполнить приведенная ниже программа. Фактически представлены две программы: при активизации первого или второго блока. В первом случае она выдает результаты численного моделирования в виде таблицы значений безразмерных скоростей и координат при фиксированном наборе параметров а, b и α, значения которых устанавливаются в разделе определения констант. При взятии в фигурные скобки первого блока и активизации второго (т.е. снятия фигурных скобок) программа выдает в графическом режиме семейство траекторий, отличающихся значениями одного из трех безразмерных параметров (в данном случае b).
Программа 148. Реализация модели «Полет тела, брошенного под углом к горизонту»
Program Pod Uglom; Uses Crt, Graph; Type G = Array[1..4] Of Real; Const A = 0; В =0.1; (параметры модели) Al = Pi / 4; (угол - параметр модели} Н = 0.001; Нрr = 0.1; (шаг интегрирования и шаг вывода результатов) Var N, I, J, M, L, К: Integer; Y0, Y: G; Х0, X, Xpr, A1, B1, Cosinus, Sinus: Real; LS: String; Function Ff(I: Integer; X: Real; Y: G): Real; {описание правых частей дифференциальных уравнений} Begin Case I Of 1: Ff:=-A1*Sinus*Y[l]-Bl*Sinus*Sqrt(Sqr(Y(l])+Sqr(Y[2]))*Y[1]; 2: Ff:=-Sinus-A1*Sinus*Y[1]-B1*Sinus*Sqrt(Sqr(Y(1])+Sqr(Y[2]))*Y[2]; 3: Ff:=Y[1]/(2*Cosinus); 4: Ff:=2*Y[2]/Sinus End End; Procedure Runge_Kut (N: Integer; Var X: Real; Y0: G; Var Y: G; Н: Real); (метод Рунге-Кутта четвертого порядка) Var I: Integer; Z, K1, K2, КЗ, К4: G; Procedure Right(X: Real; Y: G; Var F: G); {вычисление правых частей дифференциальных уравнений} Var I: Integer; Begin For I: = 1 To N Do F[I]:= Ff(I, X, У) End; Begin Right(X, Y0, K1); X:= X + Н / 2; For I:= 1 To N Do Z[I]:=Y0[I]+H*K1[I]/2; Right(X, Z, K2); For I:= 1 To N Do Z[I]:=YO[I]+H*K2[I]/2; Right(X, Z, КЗ); Х:=Х+Н/2; For I:= 1 To N Do Z[I]:= Y0[I] + H * КЗ [I]; Right (X, Z, К4); For I:= 1 To N Do Y[I]:=Y0[I]+H*(K1[I]+2*K2[I]+2*K3[I]+K4[I])/6; End; {следующий блок - для получения численных результатов при одном наборе параметров} {Begin Sinus:= Sin(Al); Cosinus:= Cos(Al); Al:= A; Bl:= B; ClrScr; N:=4; X0:=0; Y0[l]:=Cosinus; Y0[2]:=Sinus; Y0[3]:=0; Y0[4]:=0; WriteLn(' время скорость координаты'); WriteLn; X:= Х0; Xpr:= 0; Y[4]:= Y0[4]; While Y[4] >= 0 Do Begin If X >= Xpr Then Begin WriteLn ('t=', X: 6: 3, ' Vx='. Y0[l]: 6: 3, ' Vy=', Y0[2]: 6: 3. ' X=', y0[3]: 6: 3, ' Y=', Y0[4]: б: 3); Xpr:= Xpr + Hpr End; Runge_Kut(N, X, Y0, Y, H); Y0:= Y End; WriteLn; WriteLn('для продолжения нажмите любую клавишу'); Repeat Until KeyPressed End.} {следующий блок - для изображения траекторий при нескольких наборах параметров) Begin DetectGraph (J, M); InitGraph (J, M, ''); L:= 1; Al:= A; Bl:= В; Sinus:= Sin(Al); Cosinus:= Cos(Al); While L < 5 Do Begin N:= 4; (Количество уравнений в системе) Х0:= 0; Y0[l]:= Cosinus; (Начальные условия} Y0[2]:= Sinus; Y0[3]:= 0; Y0[4]:= 0: SetColor(L); Line(400, 50 + 20 * (L - 1), 440, 50 + 20 * (L - 1)); OutTextXY(450, 50 + 20 * (L - 1), '1 = '); Str(L, LS); OutTextXY(480, 50+20*(L-l), LS); X:=X0; Y[4]:=Y0[4]; While Y[4] >= 0 Do Begin Runge_Kut(N, X, Y0, Y, H); Y0:= Y; PutPixel(Abs(Trunc(Y0[3]*500)), GetMaxY-Abs(Trunc(Y0[4]*500)), L); End; Bl:= Bl * 10; L:= L + 1 End; OutTextXY(10, 50, 'для продолжения нажмите любую клавишу'); Repeat Until KeyPressed; CloseGraph End.
Приведем пример. Рассмотрим полет чугунного ядра радиуса R=0,07 м, выпущенного с начальной скоростью v0 = 60 м/с под углом α = 45° к поверхности Земли. Определим, какое расстояние пролетит ядро, на какую максимальную высоту оно поднимется, а также проследим, как изменяется скорость полета со временем. Будем решать обезразмеренные уравнения, чтобы сократить число параметров. Вычислим значения параметров а и b, после чего решим систему дифференциальных уравнений. Учтем, что плотность чугуна ρ чуг = 7800 кг/м3.
Расчеты повторялись, сначала с шагом 0,1, затем - вдвое меньшим и т.д. (хорошо известный эмпирический метод контроля точности при пошаговом интегрировании дифференциальных уравнений), пока не был получен приемлемый шаг, при котором достигается точность 10-3. Ясно, что расчеты надо проводить до тех пор, пока ядро не достигнет земли, т.е. пока Y не станет равным 0. Результаты моделирования - на рис. 7.9. В рассмотренном выше примере сопротивление среды оказывает незначительное влияние на движение тела. Проведем сравнение движения одного и того же тела без учета сопротивления среды и с его учетом, если среда достаточно вязкая (рис. 7.10).
Рис. 7.9. Графики зависимости V(τ) и Y(X) при решении задачи о полете ядра. Безразмерное значение скорости V получается по формуле Конечное значение скорости V < 1 вследствие сопротивления воздуха. Траектория движения не является параболой по той же причине
Рис. 7.10. Графики зависимости V(τ) и Y(X) при решении задачи о полете тела, брошенного под углом к горизонту, без учета сопротивления воздуха (скорость изменяется от 1 и вновь достигает значения 1; траектория - парабола) и с учетом сопротивления воздуха (конечная скорость меньше 1, и траектория - далеко не парабола) (а = 1, b = 1)
С помощью приведенной выше программы можно провести полное исследование модели в широком диапазоне значений параметров и составить качественное представление об их влиянии на изучаемое движение. Некоторые результаты иллюстрируются рис. 7.11,7.12.
Рис. 7.11. Влияние параметра а на движение тела, брошенного под углом к горизонту, при b = 0,1 (слева) и при b = 1 (справа); α = π /4 (а = 0,01; 0,1; 1; 10; кривые на рисунках соответственно располагаются справа налево)
Рис. 7.12. Влияние параметра b на движение тела, брошенного под углом к горизонту, при a = 0,1 (слева) и при а = 1 (справа); α = π /4 (b = 0,01; 0,1; 1; 10; кривые на рисунках соответственно располагаются справа налево)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.183.165 (0.011 с.) |


 -gt; раз в верхней точке vy = 0, то время достижения верхней точки на траектории
-gt; раз в верхней точке vy = 0, то время достижения верхней точки на траектории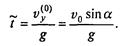

 ; за это время, двигаясь равномерно вдоль оси х со скоростью v
; за это время, двигаясь равномерно вдоль оси х со скоростью v  , тело пройдет путь
, тело пройдет путь

 (7.11)
(7.11)

 на оси х и у, получаем
на оси х и у, получаем

 , получаем уравнения движения в переменных vx, vy.
, получаем уравнения движения в переменных vx, vy. (7.12)
(7.12) (7.13)
(7.13)







 (7.14)
(7.14)
 (7.14)
(7.14)



 .
.





