
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Географическая дальность видимости горизонтаСодержание книги
Поиск на нашем сайте
Вопрос №10. Дальность видимого горизонта. Дальность видимости предмета...
Географическая дальность видимости горизонта Лучи зрения, идущие к А' и касательные к поверхности воды по всем направлениям, образуют малый круг КК', который называется линией теоретически видимого горизонта. Луч света распространяется не прямолинейно, а по некоторой кривой А'В, которая может быть аппроксимирована окружностью радиусом ρ. Явление искривления зрительного луча в атмосфере Земли называется земной рефракцией - наблюдатель видит не КК', а линию BB' - Это видимый горизонт наблюдателя. Коэффициент земной рефракции:
Угол рефракции r. Сферический радиус А'В называется географической или геометрической дальностью видимого горизонта Де. Эта дальность видимости не учитывает прозрачность атмосферы, т. е. считается, что атмосфера идеальна с коэффициентом прозрачности т = 1. Проведем через точку А' плоскость истинного горизонта Н, тогда вертикальный угол d между Н и касательной к зрительному лучу А'В будет называться наклонением горизонта
Вопрос №11. Счисление пути судна. Сущность и разновидности счисления… Счислением координат судна (счислением) называется вычисление текущих координат судна от известных координат по времени, курсу и скорости с учетом влияния ветра и течения. Навигационной прокладкой называется графическое изображение на морской карте пройденной судном части или всего маршрута, выполненное автоматически или вручную на основе измерений и вычислений. Если счисление выполняется по формулам или таблицам, оно называется аналитическим. Прокладка может быть предварительной и исполнительной. маршрут с указанием курсов, точек или ориентиров для поворота. Все это — элементы предварительной прокладки. Дальнейшая задача судоводителя сводится к обеспечению движения судна по намеченному пути и контролю за этим движением (исполнительная прокладка). При ведении прокладки решаются задачи двух видов: прямая и обратная. Невязкой места судна называется расхождение одномоментных счислимых и обсервованных мест.(С = 153° — 3,5 мили)
Графический метод учета циркуляции. прямой задаче из известной точки начала поворота В отложить перпендикулярно первому курсу величину Rц и провести из полученной точки О окружность циркуляции. линию нового курса как касательную к этой окружности. Точка касания А точка начала следования новым курсом. время поворота, по формуле: t=(T180/180)*α, α-угол поворота, Т180-вр.цирк. на 180 обратной задаче Для определения точки В — начала поворота — проведем биссектрису угла ММ1М2 и на ней найдем такое положение ножки циркуля, при котором окружность, проведенная радиусом циркуляции Rц, будет касательной к обоим курсам. Второй прием заключается в проведении двух прямых ОL и Оh, параллельных старому и новому курсам и отстоящих от них на расстоянии Rц (рис. 6.7). Дрейф судна. Учет дрейфа при прокладке Дрейфом судна называется отклонение движущегося судна с линии намеченного курса под воздействием ветра и ветрового волнения. Угол α между линией истинного курса и линией пути судна называется углом дрейфа. Угол между северной частью истинного меридиана и линией пути при дрейфе назывется путем (ПУа). Связь между ИК и ПУа выражается формулами
Определение угла дрейфа по кильватерной струе. по створу. как разность между истинным пеленгом створа и истинным курсом судна. из обсерваций. по пеленгам свободноплавающего ориентира. с помощью дрейфометра. Способ Н. Н. Матусевича. Учет дрейфа при прокладке. прямую и обратную задачи. При прямой задаче, зная ИК, рассчитывают ПУα и прокладывают линию ПУα на карте. В этом случае ПУα = ГКК + ∆ГК + α. При обратной задаче требуется рассчитать ГКК и задать его рулевому: ГКК = ПУα- α -∆ГК. Аналитический учет течения При использовании автоматических счислителей координат. β выбранный из таблиц вводится как Вопрос №12. Выбор оптимального пути… оптимальным путем между двумя и точками является тот путь, который судно проходит за кратчайшее время при минимальной затрате ресурсов, обеспечении безопасности мореплавания и сохранности перевозимых грузов. По пособиям и картам изучается район перехода. На основе этих производится выбор наивыгоднейшего маршрута перехода. Ортодромия, или ДБК, является кратчайшим расстоянием между двумя точками на земной сфере. пересекает меридианы под различными углами Кн, Ki, Kv, Kk, Разность направлений ДБК в точках А и В называется схождением меридианов УAB:
Расчет ДБК: 1. Оценка в выигрыше расстояния (S) – для этого рассчитываем Sлок = Δφ secKлок; S орт = sin φ1 sin φ2 + cosφ1cosφ2cosΔλ => ΔS = Sорт – Sлок. Если выигрыш больше 6-8ч. То исп плавание по ДБК. Расчет ДБК сводится к расчету промежуточных точек. Δλ принимается от 5-200 - плавание по хордам (19.3):
Эл-ты ДБК: Кн – угол м/у мерид. и касат к ортодр в т отхода; Кк; Sортодр Параметры ДБК: λ1,2; Ко – т, в кот ДБК пересек экватор; (φv, λv) – координаты точек вертекса(т ортодромии с наиб широтой)
Ур-е ортодромии: по этой ф-ле также рассчит промеж точки
Линия на пов-сти з, пересек-я мер-ны под 1 углом – локсодромия. На меркатор карте изобр прямой. λ2 – λ1 = tg [ ln tg (45+φ2/2) – ln tg(45+φ1/2) ] Исслед ур-я: 1 при К=0=180 - tg0=0 λ2 – λ1 = 0 локс-я совпадает с меридианом 2 К=90=270 tg90 = ∞ 0 локс-я совпадает с паралл или экв 3 0<K<90 φ=0 λ1=λ0 каждому значению φ2 будет соотв-ть только 1 знач-е λ2, т.е. локс пересек-т каждую параллель только 1 раз При всех других углах кроме 1) 2) спиралеобразная и страмится к полюсу, но не достигает.
Вопрос №13 . Визуальные методы омс По 2 пеленгам (рис. 9.1). «+» простота и быстрота определения, «-» полное отсутствие контроля при единичном определении. Поэтому критический анализ полученного места имеет решающее значение для принятия обсервации за достоверную. По 3 пеленгам При определении места по трем пеленгам в быстрой последовательности берут пеленги трех предметов А, В, С. Переводят их в истинные и прокладывают на карте. Если бы наблюдения не содержали ошибок и пеленги были взяты одновременно, то все три пеленга пересеклись бы в одной точке F, представляющей собой место судна Однако образуют так называемый треугольник погрешности. По расстояниям(10.5 10.6) По крюйс-пеленгу(11.1 11.2 11.3) Если в видимости судна имеется только один ориентир, который можно использовать для взятия пеленга. Если путь судна и пройденное расстояние известны, то, вычислив угол Θ — разность пеленгов и угол q — курсовой угол предмета А в момент первого измерения пеленга, можно рассчитать D — расстояние до предмета А в момент второго измерения пеленга. Из ∆FAF1
Так как вторая линия положения получается через элементы счисления (S и q), то место, найденное этим методом, называется счислимо-обсервованным. На практике для нахождения места судна вместо расчетов D, пользуются графическим решением (рис. 11.2). От точки пересечения с линией первого пеленга n пройденное судном расстояние S за время между пеленгами и из полученной точки m прокладывают прямую, параллельную первому пеленгу, до пересечения со вторым - приведенная линия положения; в точке пересечения этой линии со вторым пеленгом будет место судна (точка F на рис. 11.2). При наличии течения, когда элементы его известны, плавание судна между пеленгами нужно проложить с учетом действующего течения. Для этого (рис. 11.3) из произвольной точки n на первом пеленге прокладываем линию ИК судна и плавание его по лагу за время между пеленгованиями. Из полученной точки m прокладываем отрезок, равный сносу от течения за тот же промежуток времени mf = vtt, и через точку f проводим прямую, паралельную первому пеленгу. При аналитическом учете течения на линии пути необходимо отложить расстояние, пройденное судном относительно грунта:
Если за время определений судно меняло курс, то между пеленгами необходимо отложить все отрезки ИК и SЛ (рис. 11.4). СКП обсервованного места
где mл1, mл2 — средние квадратичные ошибки первой и второй линий положения; mр — средняя квадратичная ошибка приведенной линии положения, обусловленная ошибками в направлении и величине перемещения судна, средние квадратичные ошибки которых равны mк и ms
q = ПУ - ИП — угол между линией пути и первым пеленгом. По крюйс-расстоянию(11.6) Если в видимости судна имеется один ориентир и представляется возможным дважды измерить расстояние до него (по вертикальному углу или по РЛС), то место судна можно получить способом От ориентира А по направлению, параллельному линии пути судна, следует отложить пройденное расстояние SЛ. Тогда точка F2, представляющая собой место судна в момент наблюдений, может быть найдена как место пересечения двух окружностей радиусами D1 и D2, с центрами в точках А' и А. Влияние ошибок счисления будет таким же, как и в способе крюйс-пеленга. Общее графическое решение задачи определения места судна по разновременным линиям положения(11.12 11.13) Чтобы исключить ошибки счисления при омс по разновр лп, необходимо произвести четыре наблюдения и проложить полученные лп на карте. Тогда, достаточно вместить между линиями положения отрезки пути, пройденные судном по прямой, так, чтобы они относились как соответствующие промежутки времени или пройденные судном расстояния по лагу (рис. 11.12):
на кальке проводим произвольную прямую и на ней откладываем отрезки Sл1, S л2 и Sл3 (рис. 11.13). Через точки m,n,f,h и произвольную точку О проводим ОМ, ON, OF и ОН, а вблизи линии mnfh — серию параллельных прямых. Наложив кальку на карту и двигая ее, можно найти такое положение, когда все четыре точки одной из прямых, параллельных линии mnfh, будут лежать на соответствующих линиях положения и одновременно на лучах ОМ, ON, OF и ОН. Место судна на любой из линий положения на соответствующий момент помечаем уколом циркуля. ОМС по пеленгу и расстоянию при использовании радиолокатора. Расстояние может быть измерено с помощью секстана по вертикальному углу Известно, что ошибки линии положения пеленга и расстояния
По пеленгу и горизонтальному углу(12.1).
дополнительная поправка курса, а пройденное расстояние получается путем введения дополнительного коэффициента k, т. е. S = Sлk = РОЛ Клk. Вопрос №14. Использование гиперболических РНС для омс.
ОМС с помощью импульсно-фазовых РНС «Лоран-С» (США)
Cущность импульсного метода заключается в следующем. В точке приема (на судне) измеряют интервал времени ∆t = t1 – t2 между моментами прихода двух коротких импульсов, посылаемых двумя береговыми станциями. Одна из станций (А) является ведущей (Вщ), другая (В) — ведомой (Вм) (см. рис. 15.2). Разность расстояний ∆D от места судна К до радиостанций находят по формуле
Каждому значению ∆t будет соответствовать только одна гипербола. Место судна будет находиться в точке пересечения двух гипербол. Вторая гипербола получается по второй паре станций.
Что один из двух предметов закрыт для обзора, то, измерив пеленг одного предмета, можно секстаном измерить горизонтальный угол с другой точки на судне. Для получения места на карте прокладываем ИП предмета А (рис. 12.1) и затем пеленг предмета В, рассчитанный по формуле ИПВ = ИПА + α. По пеленгу и высоте светила. Если в момент взятия пеленга или радиопеленга измерить высоту светила, то место судна определяется в точке пересечения круга равных высот и линии пеленга. На практике круг равных высот заменяют высотной линией положения. Угол пересечения линий положения будет равен углу между пеленгом и направлением линии положения. Вопрос №10. Дальность видимого горизонта. Дальность видимости предмета...
Географическая дальность видимости горизонта Лучи зрения, идущие к А' и касательные к поверхности воды по всем направлениям, образуют малый круг КК', который называется линией теоретически видимого горизонта. Луч света распространяется не прямолинейно, а по некоторой кривой А'В, которая может быть аппроксимирована окружностью радиусом ρ. Явление искривления зрительного луча в атмосфере Земли называется земной рефракцией - наблюдатель видит не КК', а линию BB' - Это видимый горизонт наблюдателя. Коэффициент земной рефракции:
Угол рефракции r. Сферический радиус А'В называется географической или геометрической дальностью видимого горизонта Де. Эта дальность видимости не учитывает прозрачность атмосферы, т. е. считается, что атмосфера идеальна с коэффициентом прозрачности т = 1. Проведем через точку А' плоскость истинного горизонта Н, тогда вертикальный угол d между Н и касательной к зрительному лучу А'В будет называться наклонением горизонта
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.30.14 (0.009 с.) |




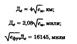

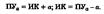

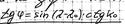
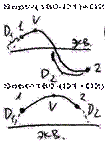


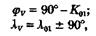









 Принцип действия. В основе работы РНС «Лоран-С» лежат импульсный и фазовый методы измерения разности расстояний
Принцип действия. В основе работы РНС «Лоран-С» лежат импульсный и фазовый методы измерения разности расстояний
 Величину ∆t определяют с помощью судового приемоиндикатора. Одной и той же разности расстояний ∆D соответствуют две изолинии (II и I’I’ на рис. 15.2), так как гипербола является кривой, симметричной относительно мнимой оси.
Величину ∆t определяют с помощью судового приемоиндикатора. Одной и той же разности расстояний ∆D соответствуют две изолинии (II и I’I’ на рис. 15.2), так как гипербола является кривой, симметричной относительно мнимой оси. Работа РНС «Лоран-С» основана на измерении промежутка времени между моментами прихода импульсов от ведущей и ведомой станций и на измерении разности фаз высокочастотных колебаний, заполняющих импульс.
Работа РНС «Лоран-С» основана на измерении промежутка времени между моментами прихода импульсов от ведущей и ведомой станций и на измерении разности фаз высокочастотных колебаний, заполняющих импульс.




