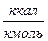Построение изобарных температурных кривых

УФА – 2007

СОДЕРЖАНИЕ:

 

Введение…………………………………………………………………….3

Исходные данные для расчета……………………………………………. 7

Построение изобарных температурных кривых, изобары, комбинированной энтальпийной диаграммы, X-Y диаграммы …………...…8

Расчет однократного испарения бинарной смеси ………………………..14

Материальный баланс ректификационной колонны……………………. 16

Тепловой баланс ректификационной колонны …………………………. 18

Расчет режима полного орошения………………………………………...19

Расчет числа теоретических тарелок по кривой равновесия…………….20

Расчет числа теоретических тарелок по тепловой диаграмме………… 21

Построение профиля температур и профиля концентраций по высоте колонны…………………………………………………………………………..23

Расчет жидкостных и паровых нагрузок по высоте колонны…………..24

Расчет фактического числа тарелок………………………………………25

Расчет высоты колонны………………………………………………… 25

Расчет диаметра колонны…………………………………………………26

Расчет диаметров штуцеров ………………………………………………29

Расчет поверхности конденсатора – холодильника……………………..30

Расчет расхода воды……………………………………………………….30

Расчет поверхности кипятильника………………………………………..31

Расчет расхода водяного пара……………………………………………..31

Заключение…………………………………………………………………33

Список использованной литературы……………………………………..35

Приложение

 

ВВЕДЕНИЕ

 

Ректификация бинарных систем является процессом разделения растворов на один или два практически чистых компо­нента путем осуществляемого в ректификационной колонне много­кратного двустороннего массообмена между движущимися про­тивотоком парами и жидкостью.

Хотя в промышленной практике сравнительно редко встре­чаются случаи разделения двухкомпонентных систем, теория ректификации бинарных смесей имеет большое познавательное значение, ибо позволяет со всей отчетливостью выявить приемы и методы исследования процесса, происходящего в ректифика­ционном аппарате, и представить результаты такого изучения на весьма наглядных расчетных диаграммах. Используя графи­ческие приемы, удается наиболее просто представить принципы расчета различных режимов работы колонны, носящие общий характер и равно приложимые и к более трудным случаям, когда разделению подвергается уже не бинарная, а значительно более сложная многокомпонентная система.

Взаимодействие фаз при ректификации представляет собой диффузию низкокипящего компонента из жидкости в пар и вы­сококипящего компонента из пара в жидкость, обусловленную разностью концентраций компонентов в массообменивающихся потоках паров и жидкости. Основным условием эффективного обмена веществом между фазами является их как можно более интенсивный контакт.

Способ контактирования фаз внутри колонны: ступенчатый (на тарелках) или непрерывный (вдоль слоя насадки), оказывает существенное влияние на глубину достигаемого разделения и на методы анализа и расчета процесса в целом.

В насадочной колонне происходит типичный противоточный дифференциальный процесс — потоки флегмы и паров находятся в постоянном взаимодействии на поверхности насадки, перенос вещества между фазами идет непрерывно. Механизм работы насадочной колонны не состоит из отдельных самостоятельных ступеней, а представляет собой непрерывное изменение концен­траций жидких и паровых потоков вдоль всей поверхности кон­такта фаз. Именно этой непрерывностью изменения составов и отличается насадочная колонна, осуществляющая истинный противоток паров и жидкости, от тарельчатой колонны, в которой составы фаз меняются скачком от одной ее тарелки к другой.

Если две неравновесные фазы, паровую и жидкую, привести во взаимный контакт и создать возможно более благоприятные условия для массопередачи, а затем после обмена веществом и энергией отделить эти фазы одну от другой каким-нибудь меха­ническим способом, то всю такую операцию в целом принято называть одной ступенью контакта. Механизм работы тарельча­той колонны, взятый в чистом виде, состоит в том, что ее тарелки действуют как ряд вполне самостоятельных ступеней контакта для встречающихся и перемешивающихся паровых и жидких потоков. Существенно, что на тарелках колонны истинный про­тивоток паров и флегмы полностью нарушается (чего не проис­ходит в насадочной колонне), и контактирующие фазы обмени­ваются веществом и энергией вследствие стремления взаимо­действующих сред к состоянию равновесия.

Чтобы установить эталон для оценки работы тарелок колонны, вводится понятие об идеальной контактной ступени или теоре­тической тарелке, характеризующейся тем, что в ходе массообмена взаимодействующие потоки достигают равновесного состояния.

Степень приближения контактирующих фаз к равновесию, реализуемая в практической ступени, условно определяется как ее эффективность или коэффициент полезного действия.

На тарелках ректификационной колонны, могущих иметь самую различную конструкцию, осуществляется интенсивное вза­имодействие между восходящим паровым и нисходящим жидким потоками. В предельном случае работы тарелки энергообмен между соприкасающимися парами и жидкостью приводит к вы­равниванию их температур, в результате обмена веществом уста­навливаются равновесные значения составов фаз, и процесс их взаимодействия прекращается, так как парожидкая система при­ходит в равновесное состояние. Пары и жидкость отделяются друг от друга, и процесс продолжается вследствие нового контак­тирования этих фаз уже на следующей ступени с другими жидкими и паровыми потоками.

В термодинамической теории массообменных процессов раз­деления при переходе от составов фаз в одном межтарелочном отделении к составам фаз в соседнем за количественную основу принимается гипотеза теоретической тарелки (ступени). Осо­бенность этой теории состоит в том, что она не занимается вопро­сом о механизме процесса и не исследует диффузионной природы и кинетической картины явления массопередачи на контактной ступени. Теория массообменных процессов разделения, основан­ная на концепции теоретической тарелки (ступени), изучает предельные условия проведения процесса и устанавливает эталоны, сравнением с которыми можно получить правильное суждение о работе практического аппарата и о степени его отклонения от наиболее совершенного в данных условиях образца.

Гипотеза теоретической тарелки не воспроизводит в точности действительной картины явления, протекающего в контактной ступени, ибо основана на статическом представлении процесса. Тем не менее эта концепция позволяет осуществить анализ и рас­чет процесса разделения исходной смеси в ректификационной колонне и получить достаточно близкую к действительности картину реального процесса, несмотря на наше неумение вполне компетентно и всесторонне исследовать сложные явления массо­передачи, происходящие на практической ступени контакта. Другим обоснованием целесо­образности разработки термо­динамической теории ректифи­кации является установивший­ся, по-видимому, окончательно взгляд, согласно которому ис следование и определение эф­фективности практических сту­пеней разделения оказывается, как правило, задачей менее трудной, чем непосредственное изучение диффузионной карти­ны процесса ректификации в ре­альной колонне. Таким образом, термодинамическая теория рек­тификации является пока пер­вой ступенью общей теории ректификации

В процессе ректификации обогатительный эффект отдельно взятых контактных ступеней, недостаточный для получения жела­тельной чистоты продуктов, увеличивается благодаря объединению группы ступеней, представляющие единый каскад — ректи­фикационную колонну, в которой и обеспечиваются условия для достижения требуемой глубины разделения.

Цель расчета ректификационной колонны состоит в том, чтобы па основе анализа ее рабочего режима и процессов, происходя­щих на контактных сту­пенях, установить для каждой из них степень обогащения фаз и тем са­мым получить возможность судить о необходимом для назначенного раз­деления числе тарелок и о составах, количествах, температурах и давлениях потоков паров и флегмы по.всей высоте колонны при установившемся режиме ее работы.

 

Исходные данные для расчета

Расчет основных показателей работы и размеров ректификационной колонны производим по следующим исходным данным:

 

― давление в середине колонны π =1,63 ата;

 

― мольная доля бензола в сырье x'_F =0,48;

 

― мольная доля отгона е'=0,52;

 

― мольная доля бензола в дистилляте y'_D=0,982;

 

― мольная доля бензола в остатке x'_W=0,037;

 

― коэффициент избытка теплоподвода n'=1,21;

 

― производительность колонны F=21,4 т/ч.

 

 

Тепловой баланс колонны

 

Без учета теплопотерь в окружающую среду все подведенное в колонну тепло: с сырьем (F·h_F) и в низ колонны через кипятильник (Q_B) отводится из колонны парами дистиллята (D·H_D), жидким остатком (W·h_W) и через конденсатор на верху колонны (Q_D).

F · h_F + Q_B = D · H_D + W · h_W + Q_D, (17)

 

Зная минимальный удельный теплоподвод (Q_B/W)_min, можем определить величину (Q_B/W):

(Q_B/W) = n'·(Q_B/W)_min, (18)

 

где n' – коэффициент избытка теплоподвода.

 

(Q_B/W) = 1,26·15200,00= 19152

Отсюда можем найти Q_B:

Q_B = (Q_B/W) · W' = 19152·96,12= 1840901,03 ккал/ч.

 

Согласно правилу рычага F, W и D лежат на одной прямой, то по энтальпийной диаграмме можем определить (Q_D/D):

(Q_D/D) = 20400 .

 

 

Отсюда можем рассчитать Q_D:

Q_D = (Q_D/D) · D' =155,5·20400= 3172138,35 ккал/ч.

 

Из энтальпийной диаграммы определим энтальпию дистиллята и остатка H_D =9400 ккал/ч и h_W = 5600 ккал/ч. Проверим сходимость теплового баланса по формуле (17):

F · h_F + Q_B = D · H_D + W · h_W + Q_D;

 

21000·7500 + 1840901,03 = 12191,9 ·9400 + 8808,1 ·5600 + 3172138,35;

159340901=167093584.

 

Расчет продолжаем, так как относительная погрешность сходимости теплового баланса составляет 4,6 %.

 

Расчет высоты колонны

 

Из опыта эксплуатации принимаем расстояние между тарелками h = 500 мм. Высота колонны рассчитываем по следующей формуле:

H = H₁ + H₂ + H₃ + (N – 2) · h, (48)

 

где N – число фактических тарелок в колонне. N = 30.

H₂ – высота зоны питания, м; H₃ – высота для самотека, м;

H₁ – высота для распределения орошения, м.

Из опыта эксплуатации принимаем H₂ = 1 м; H₃ = 1 м; H₁ = 1 м.

 

H = 1 + 1 + 1 + (30– 2) · 0,500 = 17 м.

Итак, высоту колонны принимаем H = 17000 мм.

Расчет диаметра колонны

 

Диаметр колонны рассчитывается по максимальной паровой нагрузке в верхней части колонны (из профиля паровых и жидкостных нагрузок максимальная паровая нагрузка у верхней (2) тарелки):

w_доп = 0,85 · 10^-4 · С · ((ρ^t_g – ρ_G) / ρ_G)^1/2, (45)

 

где w_доп – допустимая скорость паров в полном сечении колонны, м/с;

ρ^t_g – плотность жидкости, стекающей с первой(2) тарелки;

ρ_G – плотность пара, поступающего со второй(3) тарелки;

С – коэффициент, величина которого зависит от конструкции тарелок, расстояния между тарелками и поверхностного натяжения жидкости σ. С=900.

 

Рассчитаем объемный расход паров следующим образом:

V_G2 = G / ρ_G2, (39)

 

где ρ_G – плотность паров.

 

ρ_G2 = M_G2 / 22,4 · T₀ / (T₀ + t₂) · π, (40)

 

где T₀ – температура при н.у. T₀ = 273 K.

 

ρ_G2 = 78,84/ 22,4 · 273 / (273 + 98) · 1,55 = 4.014 кг/м³;

V_G2 = 35061,832/4.014 = 8734,048 м³/ч.

 

ρ^t_gn = (ρ²⁰_{4 g} – α · (t_n – 20)) · 1000, (42)

 

где α – средняя температурная поправка:

α = 0,001828-0,00132 · ρ²⁰_{4 g}

ρ²⁰_{4 g} – относительная плотность жидкости при 20 °С.

ρ²⁰_{4 g} = 1 / (x_n / ρ²⁰_{4 Б} + (1 – x_n) / ρ²⁰_{4 Т}), (43)

 

где ρ²⁰_{4 Б} и ρ²⁰_{4 Т} – относительные плотности соответственно бензола и толуола при 20 °С; x_n – массовая доля бензола в жидкости, стекающей с n – ной тарелки.

x_n = M_Б / M_gn · x'_n, (44)

 

 

x₂ = 78 / 79,89 · 0,865 = 0,845;

ρ²⁰_{4 g} = 1 / (0,9128 / 0,8790 + (1 – 0,9128) / 0,8669) = 0,877;

α = 0,001828-0,00132 · 0,877 = 0,0006704

ρ^t_g2 = (0,877 – 0,0006704· (98– 20)) · 1000 = 824,81кг/м³;

 

d_K = (V_G2 / (0,785 · w_доп ))^1/2, (46)

 

где d_K – диаметр колонны, м; V_G2– максимальная паровая нагрузка.

V_G =8734,048 м³/ч =2.43 м³/с.

Выбираем тарелки колпачкового типа. При максимальных нагрузках для колпачковых тарелок, расстояние между которыми принимаем h_T = 500 мм.

 

w_доп = 0,85 · 10^-4 · 900 ·((824,81 – 4,014) / 4,014)^1/2 = 1,094 м/с;

d_K = (2.43 / (0,785 · 1,094))^1/2 = 1,682 м.

 

Принимаем диаметр верхней части колонны d_K = 1,8 м.

 

Расчет диаметра штуцеров

 

Расчет расхода воды

Q_D = W · c · ∆t, (61)

W = Q_D / (c · ∆t),

 

где c – теплоемкость воды. c = 1 ккал/кг;

B – расход воды, кг/ч.

∆t = 50 – 30 = 20 °С.

B =3164363,50 / (1 · 20) = 158218,175 кг/ч.

 

Выводы

 

В ходе работы по заданным параметрам (подача сырья, содержание бензола в сырье, дистиллята и др.) был проведен расчет процесса ректификации и ректификационной колонны.

В процессе работы получены следующие результаты:

- число теоретических тарелок 16

в концентрационной части 7

в отгонной части 9

- число фактических тарелок 30

- высота аппарата 17000 мм

- диаметр колонны: 1800 мм

 

Диаметры штуцеров:

- штуцер для ввода орошения 70 мм

- штуцер вывода паров из колонны 400 мм

- штуцер ввода паров из рибойлера 350 мм

- штуцер для самотека 200 мм

- штуцер для подачи сырья 350 мм

 

Поверхность конденсатора- холодильника: 323.48 м².

Расход воды: 158218,175 кг/ч.

Поверхность кипятильника: 267.286 м².

Расход пара: 3463.05 кг/ч.

 

Список использованной литературы:

1. Касаткин А. Г. Основные процессы и аппараты химической технологии. – Москва: Химия, 1971 г.

 

2. Скобло А. И., Трегубова И. А., Молоканов Ю. К. Процессы и аппараты нефтеперерабатывающей и нефтехимической промышленности. – Москва: Химия, 1982 г.

 

3. Павлов К. Ф., Романков П. Г., Носков А. А. Примеры и задачи по курсу процессов и аппаратов химической технологии. – Ленинград: Химия, 1987 г.

 

УФА – 2007

СОДЕРЖАНИЕ:

 

Введение…………………………………………………………………….3

Исходные данные для расчета……………………………………………. 7

Построение изобарных температурных кривых, изобары, комбинированной энтальпийной диаграммы, X-Y диаграммы …………...…8

Расчет однократного испарения бинарной смеси ………………………..14

Материальный баланс ректификационной колонны……………………. 16

Тепловой баланс ректификационной колонны …………………………. 18

Расчет режима полного орошения………………………………………...19

Расчет числа теоретических тарелок по кривой равновесия…………….20

Расчет числа теоретических тарелок по тепловой диаграмме………… 21

Построение профиля температур и профиля концентраций по высоте колонны…………………………………………………………………………..23

Расчет жидкостных и паровых нагрузок по высоте колонны…………..24

Расчет фактического числа тарелок………………………………………25

Расчет высоты колонны………………………………………………… 25

Расчет диаметра колонны…………………………………………………26

Расчет диаметров штуцеров ………………………………………………29

Расчет поверхности конденсатора – холодильника……………………..30

Расчет расхода воды……………………………………………………….30

Расчет поверхности кипятильника………………………………………..31

Расчет расхода водяного пара……………………………………………..31

Заключение…………………………………………………………………33

Список использованной литературы……………………………………..35

Приложение

 

ВВЕДЕНИЕ

 

Ректификация бинарных систем является процессом разделения растворов на один или два практически чистых компо­нента путем осуществляемого в ректификационной колонне много­кратного двустороннего массообмена между движущимися про­тивотоком парами и жидкостью.

Хотя в промышленной практике сравнительно редко встре­чаются случаи разделения двухкомпонентных систем, теория ректификации бинарных смесей имеет большое познавательное значение, ибо позволяет со всей отчетливостью выявить приемы и методы исследования процесса, происходящего в ректифика­ционном аппарате, и представить результаты такого изучения на весьма наглядных расчетных диаграммах. Используя графи­ческие приемы, удается наиболее просто представить принципы расчета различных режимов работы колонны, носящие общий характер и равно приложимые и к более трудным случаям, когда разделению подвергается уже не бинарная, а значительно более сложная многокомпонентная система.

Взаимодействие фаз при ректификации представляет собой диффузию низкокипящего компонента из жидкости в пар и вы­сококипящего компонента из пара в жидкость, обусловленную разностью концентраций компонентов в массообменивающихся потоках паров и жидкости. Основным условием эффективного обмена веществом между фазами является их как можно более интенсивный контакт.

Способ контактирования фаз внутри колонны: ступенчатый (на тарелках) или непрерывный (вдоль слоя насадки), оказывает существенное влияние на глубину достигаемого разделения и на методы анализа и расчета процесса в целом.

В насадочной колонне происходит типичный противоточный дифференциальный процесс — потоки флегмы и паров находятся в постоянном взаимодействии на поверхности насадки, перенос вещества между фазами идет непрерывно. Механизм работы насадочной колонны не состоит из отдельных самостоятельных ступеней, а представляет собой непрерывное изменение концен­траций жидких и паровых потоков вдоль всей поверхности кон­такта фаз. Именно этой непрерывностью изменения составов и отличается насадочная колонна, осуществляющая истинный противоток паров и жидкости, от тарельчатой колонны, в которой составы фаз меняются скачком от одной ее тарелки к другой.

Если две неравновесные фазы, паровую и жидкую, привести во взаимный контакт и создать возможно более благоприятные условия для массопередачи, а затем после обмена веществом и энергией отделить эти фазы одну от другой каким-нибудь меха­ническим способом, то всю такую операцию в целом принято называть одной ступенью контакта. Механизм работы тарельча­той колонны, взятый в чистом виде, состоит в том, что ее тарелки действуют как ряд вполне самостоятельных ступеней контакта для встречающихся и перемешивающихся паровых и жидких потоков. Существенно, что на тарелках колонны истинный про­тивоток паров и флегмы полностью нарушается (чего не проис­ходит в насадочной колонне), и контактирующие фазы обмени­ваются веществом и энергией вследствие стремления взаимо­действующих сред к состоянию равновесия.

Чтобы установить эталон для оценки работы тарелок колонны, вводится понятие об идеальной контактной ступени или теоре­тической тарелке, характеризующейся тем, что в ходе массообмена взаимодействующие потоки достигают равновесного состояния.

Степень приближения контактирующих фаз к равновесию, реализуемая в практической ступени, условно определяется как ее эффективность или коэффициент полезного действия.

На тарелках ректификационной колонны, могущих иметь самую различную конструкцию, осуществляется интенсивное вза­имодействие между восходящим паровым и нисходящим жидким потоками. В предельном случае работы тарелки энергообмен между соприкасающимися парами и жидкостью приводит к вы­равниванию их температур, в результате обмена веществом уста­навливаются равновесные значения составов фаз, и процесс их взаимодействия прекращается, так как парожидкая система при­ходит в равновесное состояние. Пары и жидкость отделяются друг от друга, и процесс продолжается вследствие нового контак­тирования этих фаз уже на следующей ступени с другими жидкими и паровыми потоками.

В термодинамической теории массообменных процессов раз­деления при переходе от составов фаз в одном межтарелочном отделении к составам фаз в соседнем за количественную основу принимается гипотеза теоретической тарелки (ступени). Осо­бенность этой теории состоит в том, что она не занимается вопро­сом о механизме процесса и не исследует диффузионной природы и кинетической картины явления массопередачи на контактной ступени. Теория массообменных процессов разделения, основан­ная на концепции теоретической тарелки (ступени), изучает предельные условия проведения процесса и устанавливает эталоны, сравнением с которыми можно получить правильное суждение о работе практического аппарата и о степени его отклонения от наиболее совершенного в данных условиях образца.

Гипотеза теоретической тарелки не воспроизводит в точности действительной картины явления, протекающего в контактной ступени, ибо основана на статическом представлении процесса. Тем не менее эта концепция позволяет осуществить анализ и рас­чет процесса разделения исходной смеси в ректификационной колонне и получить достаточно близкую к действительности картину реального процесса, несмотря на наше неумение вполне компетентно и всесторонне исследовать сложные явления массо­передачи, происходящие на практической ступени контакта. Другим обоснованием целесо­образности разработки термо­динамической теории ректифи­кации является установивший­ся, по-видимому, окончательно взгляд, согласно которому ис следование и определение эф­фективности практических сту­пеней разделения оказывается, как правило, задачей менее трудной, чем непосредственное изучение диффузионной карти­ны процесса ректификации в ре­альной колонне. Таким образом, термодинамическая теория рек­тификации является пока пер­вой ступенью общей теории ректификации

В процессе ректификации обогатительный эффект отдельно взятых контактных ступеней, недостаточный для получения жела­тельной чистоты продуктов, увеличивается благодаря объединению группы ступеней, представляющие единый каскад — ректи­фикационную колонну, в которой и обеспечиваются условия для достижения требуемой глубины разделения.

Цель расчета ректификационной колонны состоит в том, чтобы па основе анализа ее рабочего режима и процессов, происходя­щих на контактных сту­пенях, установить для каждой из них степень обогащения фаз и тем са­мым получить возможность судить о необходимом для назначенного раз­деления числе тарелок и о составах, количествах, температурах и давлениях потоков паров и флегмы по.всей высоте колонны при установившемся режиме ее работы.

 

Исходные данные для расчета

Расчет основных показателей работы и размеров ректификационной колонны производим по следующим исходным данным:

 

― давление в середине колонны π =1,63 ата;

 

― мольная доля бензола в сырье x'_F =0,48;

 

― мольная доля отгона е'=0,52;

 

― мольная доля бензола в дистилляте y'_D=0,982;

 

― мольная доля бензола в остатке x'_W=0,037;

 

― коэффициент избытка теплоподвода n'=1,21;

 

― производительность колонны F=21,4 т/ч.

 

 

Построение изобарных температурных кривых

Для построения кривых изобар нам необходимо знать зависимость между температурой t и давлением насыщенных паров компонента Р_i, поэтому воспользуемся эмпирическим уравнением Антуана:

lg P_i = A_i – B_i / (C_i+ t), (1)

 

где А_i, В_i, С_i– эмпирические величины, постоянные для каждого компонента.

Таблица 1.1 Значение коэффициентов

 

Компонент	Ai	Bi	Ci
бензол	4,03129	1214,65	221,205
толуол	4,07427	1345,09	219,516

 

Для определения температур кипения бензола (низкокипящего компонента) t_КБ и толуола (высококипящего компонента) t_КТ, т.е. крайних точек изобарных температурных кривых, при заданном рабочем давлении уравнение Антуана нам надо решить относительно температуры t. Для этого вместо давления насыщенных паров компонента Р_iв уравнение подставим давление в середине колонны π, т.е.

t = B_i / (A_i – lg π) – C_i, (2)

 

t_КБ = B_Б / (A_Б – lg π) – C_Б = 1214,65 / (4,03129 – lg 1,63) – 221,205= 96,841 °С;

t_КТ = B_Т / (A_Т – lg π) – C_Т = 1345,09 / (4,07427 – lg 1,63) – 219,516= 128,765 °С.

 

Далее в пределах рассчитанных температур кипения компонентов зададимся

8 температурами:

 

Δt =(t_КТ – t_КБ) / 6= (128,765–96,841) / 5=6,3848 °С;

t₁ =96,841 °С

t₂ = 103,226 °С

t₃ = 109,611 °С

t₄ = 115,996 °С

t₅ = 122,38 °С

t₆ = 128,765 °С

Давления насыщенных паров компонентов Р_Б и Р_Т найдем по уравнению (1):

 

При температуре t₁ = 96,841 °C

P_Б1 = 10^{(4,03129 – 1214,65 / (221,205 +96,841))} = 1,63 ата;

P_Т1 = 10^{(4,07427 – 1345,09 / (219,516 + 96,841))} = 0,664 ата.

 

При температуре t₂ =103,226 °C

P_Б2 = 10^{(4,03129 – 1214,65 / (221,205 + 103,226))} = 1,938 ата;

P_Т2 = 10^{(4,07427 – 1345,09 / (219,516 + 103,226))} = 0,806 ата.

 

При температуре t₃ = 109,611 °C

P_Б3 = 10^{(4,03129 – 1214,65 / (221,205 + 109,611))} = 2,289ата;

P_Т3 = 10^{(4,07427 – 1345,09 / (219,516 + 109,611))} = 0,971 ата.

 

При температуре t₄ = 115,996 °C

P_Б4 = 10^{(4,03129 – 1214,65 / (221,205 + 115,996))} = 2,686 ата;

P_Т4 = 10^{(4,07427 – 1345,09 / (219,516 + 115,996))} = 1,162 ата.

 

При температуре t₅ = 122,38 °C

P_Б5 = 10^{(4,03129 – 1214,65 / (221,205 + 122,38))} = 3,134 ата;

P_Т5 = 10^{(4,07427 – 1345,09 / (219,516 + 122,38))} = 1,381 ата.

 

При температуре t₆ = 128,765 °C

P_Б6 = 10^{(4,03129 – 1214,65 / (221,205 + 128,765))} = 3,635ата;

P_Т6 = 10^{(4,07427 – 1345,09 / (219,516 + 128,765))} = 1,63ата.

 

 

Определим мольные доли бензола в кипящей жидкой фазе

x' = (π – Р_Т)/(Р_Б – Р_Т), (3)

 

в равновесной паровой фазе

y' = К_Б · x' = Р_Б / π · x', (4)

 

где К_Б – константа фазового равновесия бензола.

 

При температуре t₁ = 96,841 °С

x'₁ = (1,63 – 0,664)/(1,63 – 0,664) = 1;

y'₁ = 1,63/1,63*1=1.

 

При температуре t₂ = 103,226 °С

x'₂ = (1,63 – 0,806)/(1,938 – 0,806) = 0,73;

y'₂ = 1,938 /1,63*0,73 = 0,87.

 

При температуре t₃ = 109,611 °С

x'₃ = (1,63 – 0,971)/(2,289– 0,971) = 0,5;

y'₃ = 2,289/1,63*0,5 = 0,7.

 

При температуре t₄ = 115,996 °С

x'₄ = (1,63 – 1,162)/(2,686 – 1,162) = 0,31;

y'₄ = 2,686 /1,63*0,31 = 0,51.

 

 

При температуре t₅ = 122,38 °С

x'₅ = (1,63 – 1,381)/(3,134 – 1,381) = 0,14;

y'₅ = 3,134 /1,63*0,14 = 0,27.

 

 

При температуре t₆ = 128,765 °С

x'₂ = (1,63 – 1,63)/(3,635– 1,63) = 0;

y'₂ = 3,635/1,63*0= 0.

 

 

Для построения кривой равновесия фаз и изобарных температурных кривых составим таблицу полученных данных:

 

Таблица 1.2 Обработка данных по компоннентно

 

Температура, °С	бензол	толуол
PБ, ата	x'	y'	PТ, ата	1-x'	1-y'
t1 = tКБ = 96,841	1,63			0,628
t2 = 103,226	1,938	0,73	0,87	0,739	0,27	0,13
t3 = 109,611	2,289	0,5	0,7	0,866	0,5	0,3
t4 = 115,996	2,686	0,31	0,51	1,008	0,69	0,49
t5 = 122,38	3,134	0,14	0,27	1,169	0,86	0,73
t6= tКТ =128,765	3,635			1,55

Величины энтальпии для различных веществ в жидком и газообразном состоянии мы можем рассчитать по эмпирическим зависимостям от температуры t и относительной плотности ρ²⁰₄ вещества:

 

h_i = (0,403 + 0,000405·t) · t · (ρ²⁰₄) ^-1/2 · М, (5)

 

H_i = [(50,2 + 0,109·t + 0,00014·t²) · (4 – ρ²⁰₄) – 73,8] · М, (6)

 

где h_i и H_i – энтальпии вещества в жидком состоянии и газообразном состоянии,

M – молярная масса вещества, кг/кмоль.

 

Таблица 1.3 Физические свойства компонентов

 

Компонент	M, кг/кмоль	ρ^204
бензол		0,8790
толуол		0,8669

 

Найдем энтальпии бензола h_Б, H_Б и толуола h_Т, H_Т при различных температурах по уравнениям (5) и (6):

 

При температуре t₁ =95,031 °C

h_Б1 = (0,403 + 0,000405·95,031) · 95,031 · (0,879) ^-1/2 · 78= 3490,48 ;

H_Б1 =[(50,2 + 0,109·95,031 + 0,00014·95,031 ²) · (4 – 0,8790) – 73,8] · 78=

= 9293,60 ;

h_Т1 = [(0,403 + 0,000405·95,031) · 95,031 · (0,8669) ^-1/2]·92=4145,61 ;

H_Т1 = [(50,2 + 0,109·95,031 + 0,00014·95,031²) · (4 – 0,8669) – 73,8] · 92 =

= 11030,50 .

При температуре t₂ =100,327 °C

h_Б2 = (0,403 + 0,000405·100,327)·100,327· (0,879) ^-1/2·78 = 3702,89 ;

H_Б2 = [(50,2 + 0,109·100,327+ 0,00014·100,327²)·(4 – 0,8790) – 73,8] · 78=

= 9469,38 ;

h_Т2 = (0,403 + 0,000405·100,327)·100,327·(0,8669)^-1/2 · 92 =4397,88 ;

H_Т2 = [(50,2 + 0,109·100,327 + 0,00014·100,327²)·(4 – 0,8669)– 73,8] · 92=

= 11238,64 .

При температуре t₃ = 105,623 °C

h_Б3 = (0,403 + 0,000405·105,623)·105,623 (0,8790) ^-1/2 ·78 = 3917,19 ;

H_Б3 = [(50,2 + 0,109·105,623 + 0,00014·105,623²) · (4 – 0,8790) – 73,8] · 78

= 9647,07

h_Т3 = [(0,403 + 0,000405 ·105,623)·105,623·(0,8669)^-1/2· 92=4652,41 ;

H_Т3 = [(50,2 + 0,109·105,623 + 0,00014·105,623 ²)· (4 – 0,8669) – 73,8]·92

= 11449,03 .

При температуре t₄ =110,918 °C

h_Б4 = (0,403 + 0,000405·110,918)·110,918·(0,8790) ^-1/2· 78 = 4133,38 ;

H_Б4 = [(50,2 + 0,109·110,918 + 0,00014·110,918²)·(4 – 0,8790) – 73,8]·78

= 9826,67 ;

h_Т4 = (0,403 + 0,000405·110,918)·110,918 ·(0,8669) ^-1/2·92= 4909,17 ;

H_Т4=[(50,2+0,109·110,918+0,00014·110,918²)·(4–0,8669)–73,8]·92

=11661,69 .

При температуре t₅ =116,214 °C

h_Б5 = (0,403+ 0,000405·116,214)·116,214·(0,8790) ^-1/2 · 78 = 4351,46 ;

H_Б5 = [(50,2 + 0,109·116,214 + 0,00014·116,214²)·(4 – 0,8790) – 73,8] · 78

= 10008,18 ;

h_Т5 = (0,403 + 0,000405·116,214)·116,214·(0,8669) ^-1/2·92= 5168,18 ;

H_Т5 = [(50,2 + 0,109·116,214 + 0,00014·116,214²) · (4 – 0,8669) – 73,8] ·92

= 11876,61 .

При температуре t₆ =121,509°C

h_Б6 = (0,403 + 0,000405·121,509)·121,509·(0,8790) ^-1/2·78 = 4571,43 ;

H_Б6 = [(50,2 + 0,109·121,509+ 0,00014·121,509²) · (4 – 0,8790) – 73,8] · 78 = 10191,61 ;

h_Т6 = (0,403 + 0,000405·121,509)·121,509·(0,8669) ^-1/2·92= 5429,44 ;

H_Т6 = [(50,2 + 0,109·121,509+ 0,00014·121,509²) · (4 – 0,8669) – 73,8] · 92=

= 12093,80 .

При температуре t₇ =126,805°C

h_Б7 = (0,403 + 0,000405·126,805) ·126,805· (0,8790) ^-1/2·78 = 4793,29 ;

H_Б7 = [(50,2 + 0,109·126,805+ 0,00014·126,805²)·(4 – 0,8790) – 73,8]·78

=10376,94 ;

h_Т7 = (0,403+0,000405·126,805)*126,805·(0,8669) ^-1/2]·92=5692,94 ;

H_Т7 =[(50,2 + 0,109·126,805+ 0,00014·126,805²)·(4–0,8669) – 73,8] · 92

= 12313,24

Пренебрегая теплотой растворения, рассчитаем энтальпии жидкой и паровой фаз, имеющих равновесные составы (точнее, содержания бензола) x' и y' при заданной температуре t, по следующим уравнениям аддитивности:

для жидкой фазы

h = h_Б · x' + h_Т · (1 - x'), (7)

 

для насыщенных паров

H = H_Б · y' + H_Т · (1 - y'), (8)

 

Имея все необходимые данные, проведем расчет с помощью электронных таблиц Excel.

 

Таблица 1.4 Обработка результатов

 

параметр
PБ	1,550	1,793	2,064	2,366	2,701	3,070	3,476
PТ	0,628	0,739	0,866	1,008	1,169	1,349	1,550
x'	1,00	0,77	0,57	0,40	0,25	0,12	0,00
y'	1,00	0,89	0,76	0,61	0,43	0,23	0,00
1-x'	0,00	0,23	0,43	0,60	0,75	0,88	1,00
1-y'	0,00	0,11	0,24	0,39	0,57	0,77	1,00
hБ	3490,48	3702,89	3917,19	4133,38	4351,46	4571,43	4793,29
HБ	9293,60	9469,38	9647,07	9826,67	10008,18	10191,61	10376,94
hТ	4145,61	4397,88	4652,41	4909,17	5168,18	5429,44	5692,94
HТ	11030,50	11238,64	11449,03	11661,69	11876,61	12093,80	12313,24
h	3490,48	3863,19	4232,67	4599,71	4965,01	5329,22	5692,94
H	9293,60	9664,01	10078,86	10544,22	11066,76	11653,78	12313,24

 

Построим энтальпийную диаграмму, используя составленную таблицу рассчитанных данных.