
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о «рождественской ёлке»Содержание книги Поиск на нашем сайте
Задачи этого типа часто фигурируют под названием задачи о «рождественской ёлке» или задачи о «продавце газет», так как задача торговца ёлками или задача продавца газет состоит в том, чтобы определить, сколько ёлок заказать к рождественским праздникам или сколько газет закупить для киоска на определенный день. Это так называемые задачи управления запасами в течение одного периода. Сформулируем задачу о «рождественской ёлке» более подробно. Предположим, что продавец рождественских ёлок должен заказать партию за месяц до Рождества. После этого срока, даже если возникнет необходимость, он больше заказать не может. Таким образом, в течение сезона продавец имеет только одну возможность подачи заказа. Одна елка обходится в Пусть
так как если Задача состоит в том, чтобы найти такое Задача рождественской ёлки представляет частный случай более общей задачи, которая может быть сформулирована так. Товары можно заказать только в начале периода. Единица товаров стоит В задаче требуется определить оптимальный объём наличных запасов в начальный момент времени по критерию максимума средней прибыли за период. Если в начале периода было заготовлено единиц, то средняя прибыль равна
где В данной задаче требуется определить значение
Модель определения количества запасных частей.
При рассмотрении этой модели штрафы, связанные с дефицитом запасов считаются конечными. Кроме того, данная модель имеет следующие особенности: 1. Спрос и пополнение заказов оцениваются на основе опытных данных. 2. Рассматривается производство и потребление дискретного продукта. 3. Распределения во времени спроса и заказов на пополнение дискретные и неравномерные. 4. Известно и постоянно время выполнения заказов. Пример. Компания по производству электроэнергии собирается приобрести новый генератор для своей электростанции. Одна из основных деталей генератора весьма сложна и дорога, и целесообразно при заказе генератора заказать и несколько штук этих деталей в запас. Однако эта деталь индивидуально подгоняется для каждого генератора, и ее уже нельзя будет использовать на другом генераторе. Компания желает знать, сколько запасных частей ей следует заказывать для каждого генератора. При решении этого вопроса компания располагает следующей информацией. Стоимость одной детали, если ее заказывать вместе с генератором, составляет 500$. Отсутствие этой детали в запасе при поломке приводит к выходу генератора из строя, а простой генератора и срочный заказ детали обходятся в 10 000$. Данные о частоте выхода этой детали из строя (по 100 генераторам) приведены в таблице 3.2.1. Уравнение издержек. Составим уравнение издержек, т.е. математическую модель. Пусть в запасе имелось Число деталей, которое потребуется для ремонта генератора, заранее неизвестно, однако вероятности выхода из строя определенного числа деталей Чтобы вычислить ожидаемые при данном уровне запасов затраты, необходимо просуммировать значения расходов для каждого
Таблица 3.2.1
Подсчитаем сначала численно ожидаемый суммарный расход при различных, но разумных уровнях запасов (т.е. от 0 до 5). Будем считать, что убыток от неиспользованных запасных деталей равен их покупной стоимости, так как расходы на хранение пренебрежимо малы. Таким образом Произведя с помощью этого уравнения расчеты для различных уровней запасов, получаем следующие значения для ожидаемых суммарных расходов:
Это показывает, что оптимальный уровень запасов равен 2. Рассмотрим аналитическое решение этой задачи. Определим величину S, при которой ожидаемые суммарные доходы будут минимальными
Положим в этом уравнении
Но Отсюда получаем
Точно также можно получить, что
Определим теперь
Для любого целого Поэтому Таким образом, определено значение
Если
то из уравнения для определения
Если же
то из уравнения для определения
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 598; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.198 (0.008 с.) |

 долларов, а продаётся за
долларов, а продаётся за 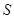 долларов. Затраты за непроданные до конца сезона ёлки составляют итоговые потери из-за нереализованных товаров.
долларов. Затраты за непроданные до конца сезона ёлки составляют итоговые потери из-за нереализованных товаров. означает вероятность того, что за сезон потребуется
означает вероятность того, что за сезон потребуется  елей. Если к началу сезона было заготовлено
елей. Если к началу сезона было заготовлено  деревьев, то
деревьев, то  математическое ожидание прибыли за сезон составит
математическое ожидание прибыли за сезон составит ,
, , то годовой доход равен
, то годовой доход равен  , если
, если  , то за проданные ёлки будет получено
, то за проданные ёлки будет получено  долларов.
долларов.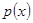 – вероятность того, что за период потребуется
– вероятность того, что за период потребуется  штук. Если в момент возникновения требования на складе нет товаров, то помимо недополученной прибыли, фирма терпит убытки, связанные с потерей предпочтения, которые можно оценить
штук. Если в момент возникновения требования на складе нет товаров, то помимо недополученной прибыли, фирма терпит убытки, связанные с потерей предпочтения, которые можно оценить  долларов в пересчёте на единицу товара. Все товары, не распроданные к концу периода, могут быть реализованы по цене
долларов в пересчёте на единицу товара. Все товары, не распроданные к концу периода, могут быть реализованы по цене  долларов
долларов  .
.









 -средний спрос за период.
-средний спрос за период.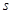 деталей, а за все время эксплуатации генератора потребовалось
деталей, а за все время эксплуатации генератора потребовалось 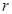 деталей. Тогда запасу в
деталей. Тогда запасу в 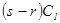 . Если
. Если 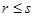 , то запас оказался чрезмерным и
, то запас оказался чрезмерным и 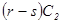 , если
, если 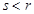 , т.е. запасных деталей не хватило.
, т.е. запасных деталей не хватило.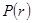 мы знаем.
мы знаем.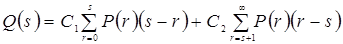 .
.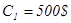 . Нехватка запасных деталей обходится в
. Нехватка запасных деталей обходится в 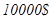 за одну штуку – такова плата за простой генератора и срочный заказ недостающей детали.
за одну штуку – такова плата за простой генератора и срочный заказ недостающей детали.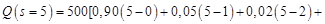
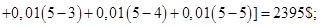
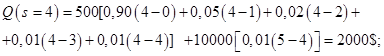
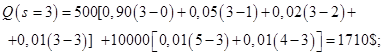
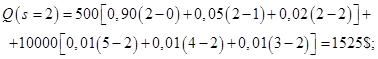
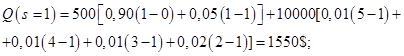
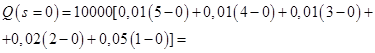
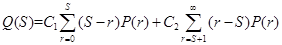 .
.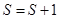 , тогда
, тогда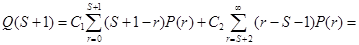
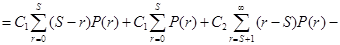
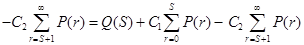 .
.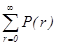 =1 или
=1 или 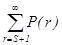 =1-
=1- 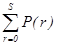 .
.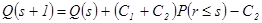 .
.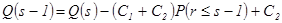 .
.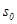 , при котором
, при котором 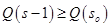 и
и 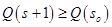 . Для этого, как видно из соотношений, определяющих
. Для этого, как видно из соотношений, определяющих 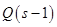 и
и 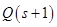 , необходимо, чтобы
, необходимо, чтобы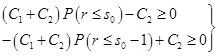 .
.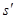 , большего
, большего 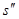 , меньшего
, меньшего 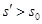
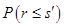 будет больше
будет больше 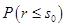
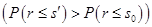 , а при
, а при 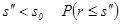 будет меньше
будет меньше 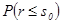 .
.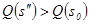 при любом
при любом 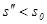 и
и 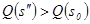 при любом
при любом 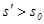 .
.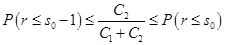 .
.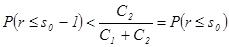 ,
,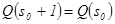 .
.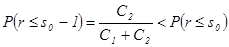 ,
,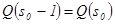 .
. 


