
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача проектирования судов как экспериментальная задача математического проектированияСодержание книги
Поиск на нашем сайте
Широкое применение вычислительной техники в задачах проектирования судов стало возможным благодаря формулировке задачи проектирования как экспериментальной задачи математического проектирования. Они записываются следующим образом: Пусть задан вектор исх. данных с(с1, с2,….)компонентами этого вектора м.б. параметры ТЗ (с1=mгр; c2=v; c3=Mгр….) отыскивается вектор оптимизированных переменных х(х1, х2,….) где компонентами этого вектора являются искомые гл. элементы судна (x1=L, x2=B, x3=T…..), при чём на вектор x накидываются двусторонние ограничения вида
Кроме этого на компоненты вектора x накладываются односторонние ограничения типа
j- какое либо регламентируемое качество судна связанное с требования регистра; G- в зависимости от (x,c) функционал которая описывает требования к g-качество; А- функционал самого j качества.
В этом случае можно записать исходя из «Правил регистра» Аi=0,25м Любое решение полученных равенств и неравенств относительно вектора искомых параметров будет удовлетворять, решению задачи, однако из множества решений надо выбрать одно которое наилучшим образом соответствует поставленной задаче. Для того, чтобы определить термин «наилучшим образом» необходимо выбрать критерий эффективности или функцию цели Z(x,c). Этих критериев может быть один или несколько в зависимости от желания проектанта(Dà min или Nàmin). Функция цели может быть провозоспособность судна Пà min и т.д. Z(x,c)à Extr Т.О. задачу проектирования можно сформулировать следующим образом: при заданном векторе исходных данных с требуется найти: - вектор исходных переменных х удовлетворяющие односторонним и двусторонним неравенствам, при чём найти т.о., при найденных значениях х обращалось в Еxtr.-мум, а именно так формулируется Extr- мальные задачи математического програмирования. Пример: Построить математическую модель проектирования грузового судна. Компоненты вектора с примем следующими. С1=mгр* -требуемая грузоподъёмность судна; С2=Мгр*-грузовместимость; С3=v*- скорость судна; С4=r*- дальность плавания; С5=nэк- численность экипажа судна. Компоненты вектора х искомых данных примем: Х1=D
X3=δ X4=В/Т X5=Н/Т Замечания: В принципе можно принять и другие значения вектора искомых переменных X1=L; X2=B; X3=T; X4=H…. 1. В первом приближении определить D можно используя ηгр- коэффициент утилизации по грузоподъёмности:
Если мы хотим организовать двусторонние ограничение, то
Ε- среднеквадратическое отклонение тогда запишем
2. Скорость хода судна должна v=v* v- фактическая скорость хода; Скорость хода определяется по формуле:
3. Грузоподъёмность судна д.б. не менее требуемой
4. Удельная грузоподъёмность д.б. не менее требуемой
5. Относительная поперечная метацентрическая высота д.б. менее определяемой требования регистра
6. Собственный период качки судна д.б. не менее допустимого по условиям обитаемости.
7. Минимальная высота надводного борта д.б. не менее регламентируемой «Правилами регистра»
Т.О. получим систему из одного уравнения и семи неравенств. В качестве критерия эффективности примем абсолютные приведённые затраты Z=EK+Q Е- нормативный коэффициент эффективности капитала вложений (0,12)i К- строительная стоимость судна
Сi- стоимость единицы массы соответствующего раздела нагрузки; Q- эксплуатационные расходы; Q=Q1+Q2+Q3+Q4 Q1 – расходы зависящие от строительной стоимости судна Q2 – расходы на экипаж Q3 – расходы на топливо и смазку Q4 – косвенные расходы В полученных уравнениях и неравенствах все обозначения переводятся на символы векторы с и х, а решение системы уравнений и неравенств позволяет получить все искомые главные элементы судна, причём такие, которые приведут к min приведённых затрат.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.141 (0.009 с.) |



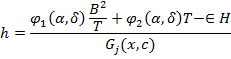
 - относительная длина
- относительная длина
 и
и 
 - математическое ожидание коэффициента утилизации
- математическое ожидание коэффициента утилизации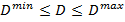




 отсюда
отсюда








 - коэффициент учитывающий серийность постройки судов;
- коэффициент учитывающий серийность постройки судов;


