
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое выражение для кривой ЛиссажуСодержание книги Поиск на нашем сайте
где A, B – амплитуды колебаний, a, b – частоты, δ – сдвиг фаз. Вид кривой сильно зависит от соотношения a / b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии Фигуры Лиссажу, где
являются полиномами Чебышева первого рода степени Фигуры Лиссажу можно наблюдать, например, на экране электронно-лучевого осциллографа, если к двум парам отклоняющих пластин подведены переменное напряжения с равными или кратными периодами. Вид фигур Лиссажу позволяет определить соотношения между периодами и фазами обоих колебаний. Если колебания, которые совершает точка, происходят не по гармоническому, а по более сложному закону, но с одинаковым периодом, то получаются замкнутые траектории, аналогичные фигурам Лиссажу но искажённой формы. По виду этих фигур можно судить о форме колебаний. Таким образом, наблюдение фигур Лиссажу – удобный метод исследования соотношений между периодами и фазами колебаний, а также и формы колебаний. Теория лабораторной работы Для определения частоты неизвестного гармонического колебания часто используется метод фигур Лиссажу, который заключается в следующем: исследуемое колебание складывается с взаимно-перпендикулярным ему колебанием известной частоты. В общем случае в результате сложения получаются фигуры Лиссажу, по общему виду которых можно определить частоты исследуемого напряжения. В настоящей работе сравнение частот производится с помощью электронного осциллографа, на вертикально отклоняющие пластины которого подается исследуемое напряжение от источника колебаний звуковой частоты, а на горизонтально отклоняющие пластины - напряжение определенной частоты от другого генератора. Рассмотрим два взаимно-перпендикулярных колебания
где Система уравнений (5) представляет собой уравнение кривой, являющейся результатом сложения этих колебаний, заданной в параметрической форме. Определим уравнение траектории точки, участвующей в данных колебаниях, исключая из уравнения (5) время
Прибавим к левой и правой части (6) минимальную величину
По формуле Муавра: Продолжим преобразования:
Но Подставляя эти значения в формулу (7), получим:
Разлагая по биному Ньютона выражение в квадратных скобках и приравнивая действительные части слева и справа, получим уравнение траектории колеблющейся точки. Рассмотрим частный случай - сложение колебаний с одинаковыми частотами
Откуда: Это уравнение в общем случае является уравнением эллипса. Рассмотрим частные случаи этого уравнения. Пусть колебания происходят с разностью фаз равной нулю или
т.е. эллипс вырождается в прямую (рис. 7).
 . Тогда уравнение (9) будет иметь вид: . Тогда уравнение (9) будет иметь вид:  . .
 . В тех случаях, когда . В тех случаях, когда  , по общему виду уравнения результирующего колебания, получаемого по формуле (8), трудно судить о форме траектории. , по общему виду уравнения результирующего колебания, получаемого по формуле (8), трудно судить о форме траектории.
Пусть показатель степени в уравнении (8) есть число рациональное, т, е. может быть представлено в виде отношения двух целых чисел
Из системы уравнений (5) следует, что:
где
Отсюда следует, что за промежуток времени После истечения времени Пусть Выведем правило нахождения отношения частоты по фигурам Лиссажу. Учитывая уравнение (10), можно переписать уравнение (8) в виде:
 . Тогда, возводя левую и правую части по биному Ньютона и приравнивая действительные части, получим уравнение . Тогда, возводя левую и правую части по биному Ньютона и приравнивая действительные части, получим уравнение 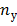 – степени относительно – степени относительно 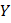 , имеющее , имеющее 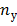 корней. Графически это означает, что ось корней. Графически это означает, что ось 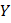 пересекает кривую пересекает кривую 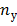 раз. Если раз. Если  , где , где 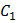 – произвольная постоянная, то получим так же уравнение, имеющее – произвольная постоянная, то получим так же уравнение, имеющее 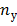 корней. корней.
Фигура Лиссажу будет пересекать Полагая
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.01 с.) |

 ,
, и отрезка прямой
и отрезка прямой  . Ещё один пример фигуры Лиссажу – парабола
. Ещё один пример фигуры Лиссажу – парабола 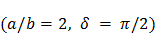 .
. – рациональное число.
– рациональное число. ,
,  (
(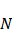 – натуральное число) и
– натуральное число) и (4)
(4)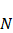 .
.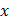 и
и  с частотами
с частотами  и
и  .
. (5)
(5) - начальная разность фаз между колебаниями. Очевидно,
- начальная разность фаз между колебаниями. Очевидно, 
 :
: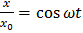 ;
;  , где
, где  (6)
(6)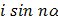 , получим:
, получим: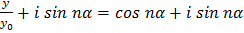 .
. .
. .(7)
.(7) ;
; 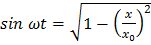 .
. .(8)
.(8) ,
,  ,
,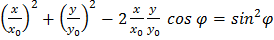 . (9)
. (9) . В этом случае уравнение (9) принимает вид:
. В этом случае уравнение (9) принимает вид:
 , или
, или  ,
, Рис. 7.
Рис. 7.
 Рис. 8.
Рис. 8.
 и
и 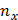 :
: .
. ,
, и
и  – частота и период колебаний в направлении оси
– частота и период колебаний в направлении оси 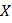 ;
;  и
и  – частота и период колебаний в направлении оси
– частота и период колебаний в направлении оси  .
. полных колебаний в направлении оси
полных колебаний в направлении оси  полных колебаний в направлении оси
полных колебаний в направлении оси 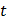 точка будет находиться в той же фазе, что и в начальный момент, т. е. за следующий промежуток времени
точка будет находиться в той же фазе, что и в начальный момент, т. е. за следующий промежуток времени  колебания в точности повторятся. В результате колебания будут накладываться сами на себя и дадут устойчивую картину (фигуры Лиссажу). Если же одно из чисел
колебания в точности повторятся. В результате колебания будут накладываться сами на себя и дадут устойчивую картину (фигуры Лиссажу). Если же одно из чисел  нельзя представить в виде отношения целых чисел, то это приведет к добавочной разности фаз. В результате картина результирующего колебания будет непрерывно изменяться. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого. Такое сравнение частот можно проделать осциллографическим методом, подавая на горизонтально отклоняющие пластины напряжение с известной частотой
нельзя представить в виде отношения целых чисел, то это приведет к добавочной разности фаз. В результате картина результирующего колебания будет непрерывно изменяться. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого. Такое сравнение частот можно проделать осциллографическим методом, подавая на горизонтально отклоняющие пластины напряжение с известной частотой  а на вертикально отклоняющие пластины – исследуемое напряжение с частотой
а на вертикально отклоняющие пластины – исследуемое напряжение с частотой  .
.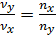 , тогда:
, тогда:  . (10)
. (10) .
. Рис. 9.
Рис. 9.
 , получим уравнение
, получим уравнение 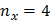 и
и  . Следовательно,
. Следовательно, 



