
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная форма закона ФарадеяСодержание книги Поиск на нашем сайте
В дифференциальной форме закон Фарадея можно записать в следующем виде:
В интегральной форме (эквивалентной):
Здесь Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже). В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно). 1.3. Явление самоиндукции Самоиндукция – возникновение эдс индукции При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, в результате чего в нём возбуждается эдс – эдс самоиндукции. Направление эдс самоиндукции определяется правилом Ленца, т. е. при увеличении тока в цепи эдс самоиндукции препятствует возрастанию тока, а при уменьшении тока – его убыванию. Таким образом, самоиндукция подобна явлению инерции в механике. Эдс самоиндукции
Коэффициент пропорциональности В электрической цепи, содержащей постоянную эдс, при замыкании цепи сила тока за счёт эдс самоиндукции устанавливается не мгновенно, а через некоторый промежуток времени, а при размыкании цепи ток не прекращается мгновенно; возникающая при размыкании цепи эдс самоиндукции может во много раз превысить эдс источника. В цепи переменного тока вследствие самоиндукции сила тока в катушке, обладающей индуктивностью, отстаёт по фазе от напряжения на концах катушки на Явление самоиндукции играет важную роль в электротехнике и радиотехнике. Благодаря самоиндукции происходит перезарядка конденсатора, соединённого последовательно с катушкой индуктивности, в результате в контуре возникают свободные электромагнитные колебания. 1.4. Индуктивность Величина магнитной индукции
где Индукти́вность (или коэффициент самоиндукции) (от лат. inductio – наведение, побуждение) – коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. Индуктивность подобно электроемкости, зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник. Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём силы тока:
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с. Нередко говорят об индуктивности прямого длинного провода. В этом случае и других полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля. Единицу индуктивности в СИ называют генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В: 1 Гн = 1 В / (1 А/с) = 1 В·с/А = 1 Ом·с. 1.5. Соленоид
Солено́ид (от греч. solen – трубка и eidos – вид) – это однослойная катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра; система круговых токов, центры которых лежат на одной прямой (рис. 9). Магнитное поле соленоида аналогично магнитному полю полосового магнита. Соленоид с током представляет собой электромагнит. Соленоид
Соленоид на постоянном токе Если длина соленоида намного больше его диаметра и не используется магнитный материал, то при протекании тока по обмотке внутри катушки создаётся магнитное поле, направленное вдоль оси, которое однородно и для постоянного тока по величине равно: При протекании тока соленоид запасает энергию, равную работе, которую необходимо совершить для установления текущего тока
При изменении тока в соленоиде возникает ЭДС самоиндукции. Индуктивность соленоида Индуктивность соленоида выражается следующим образом:
где Без использования магнитного материала плотность магнитного потока
где
Отсюда следует формула для индуктивности соленоида:
эквивалентная предыдущим двум формулам. Теория лабораторной работы
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.007 с.) |

 .
. .
. – напряжённость электрического поля,
– напряжённость электрического поля,  – магнитная индукция,
– магнитная индукция,  – произвольная поверхность,
– произвольная поверхность,  – её граница. Контур интегрирования
– её граница. Контур интегрирования  в проводящем контуре при изменении в нём силы тока; частный случай индукции электромагнитной.
в проводящем контуре при изменении в нём силы тока; частный случай индукции электромагнитной. пропорциональна скорости изменения силы тока
пропорциональна скорости изменения силы тока  и индуктивности
и индуктивности  контура:
контура:
 .
.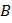 , создаваемой током в любом замкнутом контуре, пропорциональна силе тока
, создаваемой током в любом замкнутом контуре, пропорциональна силе тока  . Так как магнитный поток
. Так как магнитный поток  пропорционален
пропорционален  ,
, – коэффициент пропорциональности между током в проводящем контуре и созданным им магнитным потоком, пронизывающим этот контур. Величину
– коэффициент пропорциональности между током в проводящем контуре и созданным им магнитным потоком, пронизывающим этот контур. Величину  .
. Рис. 9. Образование магнитного потока в соленоиде
Рис. 9. Образование магнитного потока в соленоиде
 Рис.10.
Рис.10.
 , где
, где  – магнитная проницаемость вакуума,
– магнитная проницаемость вакуума,  – число витков N на единицу длины
– число витков N на единицу длины  (линейная плотность витков),
(линейная плотность витков),  .
. ,
, – объём соленоида,
– объём соленоида,  – длина проводника, намотанного на соленоид,
– длина проводника, намотанного на соленоид,  – длина соленоида,
– длина соленоида,  – диаметр витка.
– диаметр витка. в пределах катушки является фактически постоянной и равна:
в пределах катушки является фактически постоянной и равна: ,
,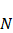 − число витков,
− число витков,  , умноженному на площадь поперечного сечения и число витков
, умноженному на площадь поперечного сечения и число витков  ,
, ,
,


