
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эндогенный технический прогрессСодержание книги Поиск на нашем сайте
Так как технический прогресс чаще всего связан со значительными затратами общества на научные исследования, образование и техническое обновление производства, то он сам зависит от уровня развития экономики. Поэтому более адекватное представление о механизме функционирования растущей экономики дают модели, в которых технический прогресс является эндогенным параметром. В качестве примера учета технического прогресса в виде эндогенного фактора рассмотрим модель экономического роста с производственной функцией, в число аргументов которой, кроме труда и физического капитала, входит и «человеческий капитал»6. Под ним в данном случае подразумевают особые способности работника, повышающие результативность его труда и приобретенные вследствие затрат на получение образования и квалификации. В экономике, имеющей постоянный темп прироста населения и предложения труда (n), технология производства отображается производственной функцией Кобба—Дугласа:
где H – объем человеческого капитала, измеряемого в условных единицах «образованности», наподобие того, как физический капитал измеряется в единицах некоторого стандартного вида техники. Хозяйство ведется в условиях совершенной конкуренции, поэтому факторы производства оплачиваются по ценам, равным их предельным производительностям
Представительное домашнее хозяйство распределяет все имеющееся у него время (Т), сверх необходимого для отдыха, между работой (N) и учебой (E). Поэтому уравнение бюджета времени i -го домашнего хозяйства имеет вид
Объем приобретаемого за время учебы человеческого капитала зависит не только от выделенного индивидом времени, но и от количества произведенного государством общественного блага (B) – инфраструктуры образования, измеряемого объемом затрат на его производство
Формула (14.7) есть производственная функция создания человеческого капитала. Общественным благом все население может пользоваться бесплатно; его производство финансируется за счет подоходного налога. Цель домашнего хозяйства – распределить свое время между трудом и учебой так, чтобы максимизировать доход от труда и человеческого капитала. Формально задача состоит в том, чтобы максимизировать сумму (wNi + hHi) при ограничениях (14.6) и (14.7). Для решения задачи составим функцию Лагранжа
Она достигает максимума при
Подставив формулы (14.8) и (14.9) в выражение (14.10), после преобразований получим
Из производственной функции (14.7) следует, что
Поэтому условие максимизации дохода отдельным домашним хозяйством (14.11) можно записать в виде
Поскольку при заданной технологии
где X – число всех домашних хозяйств. Из равенств (14.12) и (14.13) следует, что
Таким образом, пропорция, в которой представительное домашнее хозяйство распределяет имеющееся у него время между работой и учебой, постоянна и зависит только от технологии производства национального дохода и общественного блага; так как Ni + Ei = T = const, то и число часов, уделяемое работе и учебе, не изменяется во времени: Запишем равенство (14.11) в темпах прироста:
Соответственно из условия:
Равенство (14.16) выражает зависимость между темпами роста человеческого капитала и общественного блага. Приращение последнего за период равно собираемым за этот срок налогам
Прирост физического капитала за период равен объему сбережений
Поскольку рост предложения труда экзогенно задан, то зависимости (14.17) и (14.18) определяют возможности стабильного роста национального дохода, производимого по технологии
Можно доказать7, что в рассматриваемой модели устойчивое динамическое равновесие наступает при постоянных коэффициентах капиталоемкости (K/y) и «образованиеемкости» (B/y) национального дохода. С учетом этого определим величину равновесного темпа прироста. Запишем уравнение производственной функции в темпах прироста
Так как
Следовательно, равновесный темп прироста национального дохода
Так как gm > 0, то g > n, т.е. темп роста национального дохода превышает темп роста трудовых ресурсов. Поскольку равновесный темп роста не зависит от нормы сбережений и ставки подоходного налога, то можно определить их значения, максимизирующие фонд потребления при равновесном росте8
Оптимальная норма сбережений тем меньше, а оптимальная ставка подоходного налога для финансирования производства общественного блага тем больше, чем эластичней производство национального дохода по объему общественного блага.
Краткие выводы Цель построения теоретических моделей экономического роста – определить условия, обеспечивающие равенство между совокупным спросом и совокупным предложением в растущей экономике и совместимость динамического равновесия с полной занятостью. Исследования основаны на различных исходных предпосылках посткейнсианских и неоклассических моделей приводят к взаимопротивоположным выводам относительно устойчивости равновесного роста и факторов, определяющих его темп. Неустойчивость экономического роста в модели Харрода—Домара вытекает из трех ее исходных предпосылок: невзаимозаменяемости факторов производства, жесткости их цен и экзогенно заданной нормы сбережений. Из-за отсутствия в модели Калдора двух последних предпосылок в ней достигается устойчивый рост при технологии Леонтьева. В неоклассических моделях устойчивый рост существует при экзогенной норме сбережений в результате взаимозаменяемости факторов производства и гибкости их цен. Из посткейнсианских моделей следует, что при данной технике темп экономического роста определяется величиной предельной склонности к сбережению и равновесный рост может сопровождаться неполной занятостью. В неоклассической модели темп экономического роста при отсутствии технического прогресса определяется темпом прироста трудовых ресурсов. Изменение нормы сбережений меняет только капиталовооруженность и производительность труда, оставляя в длинном периоде темп равновесного роста постоянным. Из независимости равновесного темпа роста национального хозяйства от нормы сбережений вытекает проблема ее оптимизации. При отсутствии технического прогресса максимальный рост потребления на душу населения достигается тогда, когда предельная склонность к сбережению равна эластичности выпуска по капиталу. Поскольку главным фактором экономического роста является технический прогресс, то процессы, происходящие в растущей экономике, наиболее адекватно отображаются посредством моделей, учитывающих его. Это достигается путем включения в производственную функцию модели дополнительного аргумента, изменяющегося во времени экзогенно или эндогенно. Основными целями изучения последствий технического прогресса в теории экономического роста являются определение условий его совместимости с равновесным ростом и его влияние на функциональное распределение национального дохода. Экзогенный технический прогресс называют нейтральным, если он не изменяет функциональное распределение национального дохода. Существуют три разновидности нейтрального технического прогресса. Нейтральность по Хиксу достигается за счет того, что он не изменяет ни капиталовооруженность труда, ни соотношение предельных производительностей факторов производства. Нейтральность по Харроду обеспечивается за счет того, что по мере развития технического прогресса каждому значению средней производительности капитала соответствует неизменная предельная его производительность. При нейтральности по Солоу по мере развития технического прогресса каждому значению средней производительности труда соответствует неизменная предельная его производительность. С равновесным ростом совместим нейтральный по Харроду технический прогресс. Он характеризуется тем, что капиталовооруженность и производительность труда растут с постоянным темпом.
Математическое приложение: Определение условий равновесного роста экономики при эндогенном техническом прогрессе Обозначим
Учитывая зависимости (14.17) и (14.18), получим
Умножим обе части равенства (1) на h
Из равенств (14.17), (14.18) и (14.19) также следует, что
Умножим обе части равенства (3) на n
В состоянии динамического равновесия
Поскольку Определим значения s и t, максимизирующие фонд потребления. Поскольку при равновесном росте
то объем потребления можно представить в виде
Фонд потребления достигает максимума при
Подставив в найденные условия максимизации фонда потребления значения
1 World Economic Outlook, October. 2001. IWF. www.iwf.org.
2 Р. Харрод и Е. Домар независимо друг от друга построили простейшую модель экономического роста, соответствующую кейнсианской концепции функционирования национальной экономики. Harrod R. An essay in dynamic theory // Economics. Journal, 1939. Mar. Vol. 49; Domar E. Expansion and employment // American Economic Review, 1947. Mar. Vol. 37.
3 Kaldor N. A model of economic growth // Economics Journal, 1957. Dec. Vol. 67.
4 Solow R. A contribution to the theory of Economic Growth // Quart. J. Econ., 1956. Vol. 70. 5 Swan T. Economic Growth and Capital Accumulation // Economic Record, 1956. Vol. 32.
6 Schultz T. Investment in human capital // American Economic Revien, 1987. Vol. 77; Maussner A., Klump R. Wachstumtheorie. Berlin, 1996. S. 72—77.
7 См. Математическое приложение к данной главе. 8 Там же.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.104 (0.007 с.) |

 ,
, .
. (14.6)
(14.6) . (14.7)
. (14.7)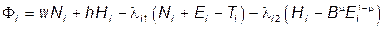 .
.
 . (14.11)
. (14.11) .
. . (14.12)
. (14.12)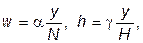 то
то  . (14.13)
. (14.13) . (14.14)
. (14.14)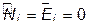 .
. ; так как
; так как  , то
, то . (14.15)
. (14.15) и
и  следует, что
следует, что 
 . Отсюда:
. Отсюда:  . Поэтому равенство (14.15) можно записать в виде
. Поэтому равенство (14.15) можно записать в виде . (14.16)
. (14.16) . (14.17)
. (14.17) . (14.18)
. (14.18) .
.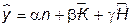 . (14.19)
. (14.19) , а
, а  .
. (14.20)
(14.20) .
. . Тогда с учетом (14.16) и (14.19) получаем
. Тогда с учетом (14.16) и (14.19) получаем
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) . Поэтому равновесные значения коэффициентов капиталоемкости и «образованиеемкости» национального дохода находятся из следующей системы уравнений:
. Поэтому равновесные значения коэффициентов капиталоемкости и «образованиеемкости» национального дохода находятся из следующей системы уравнений:
 и
и  , то
, то  и
и  .
. ,
, .
.
 и учитывая равенства (14.20) и
и учитывая равенства (14.20) и 



