Уравнение Фредгольма II-го рода с симметричным ядром. Связь с краевой задачей
Рассмотрим уравнения Фредгольма II-го рода:  , ,  . с непрерывным ядром . с непрерывным ядром  и непрерывной правой частью и непрерывной правой частью  . .
Опр: Ядро  интегрального оператора Фредгольма называется симметричным, если интегрального оператора Фредгольма называется симметричным, если 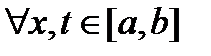 справедливо равенство: справедливо равенство:  . Обозначим интегральный оператор Фредгольма через A: . Обозначим интегральный оператор Фредгольма через A: 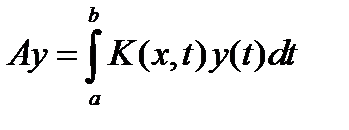 . И вспомним определенние характаристического числа: Числа . И вспомним определенние характаристического числа: Числа  , при которых однородное уравнение , при которых однородное уравнение 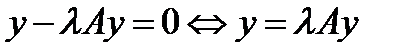 имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида  называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу  . .
Теорема Пусть  и и  , ,  – заданные функции, и однородная задача: – заданные функции, и однородная задача:  (59), (59),  (60), (60),  (61) не имеет других решений, кроме тождественного нуля. Тогда задача Штурма–Лиувилля: (61) не имеет других решений, кроме тождественного нуля. Тогда задача Штурма–Лиувилля:  , ,  , ,  эквивалентна интегральному уравнению: эквивалентна интегральному уравнению:  (63), где (63), где  функция Грина задачи (59) – (61), а функция Грина задачи (59) – (61), а  т.е. y(x) является собственной функцией задачи (62), (60), (61), соответствующей собственному значению т.е. y(x) является собственной функцией задачи (62), (60), (61), соответствующей собственному значению  , тогда и только тогда, когда y(x) является собственной функцией уравнения (63), соответствующей характеристическому значению , тогда и только тогда, когда y(x) является собственной функцией уравнения (63), соответствующей характеристическому значению  . .
Док: По теореме Гильберта (билет 13) существует функция Грина задачи (59) – (61), причём решение задачи (62), (60), (61), если правую часть  рассматривать как известную функцию, представляется в виде: рассматривать как известную функцию, представляется в виде: 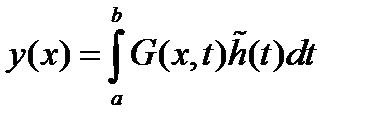 (64), откуда (64), откуда  = =  . Итак, пара . Итак, пара  есть собственная функция задачи (62), (60), (61) и соответствующее ему собственное значение тогда и только тогда, когда пара есть собственная функция задачи (62), (60), (61) и соответствующее ему собственное значение тогда и только тогда, когда пара  есть собственная функция уравнения (63) и соответствующее есть собственная функция уравнения (63) и соответствующее
ему характеристическое значение. Замечание Напомним, что функция Грина всегда симметрична, поэтому получаемое интегральное уравнение
 есть уравнение с симметричным ядром. есть уравнение с симметричным ядром.
27. Уравнение Фредгольма II-го рода с симметричным ядром. Симметричность оператора
Рассмотрим уравнения Фредгольма II-го рода:  , ,  . с непрерывным ядром . с непрерывным ядром  и непрерывной правой частью и непрерывной правой частью  . .
Опр: Ядро  интегрального оператора Фредгольма называется симметричным, если интегрального оператора Фредгольма называется симметричным, если 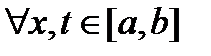 справедливо равенство: справедливо равенство:  . Обозначим интегральный оператор Фредгольма через A: . Обозначим интегральный оператор Фредгольма через A: 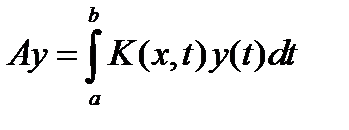 . И вспомним определенние характаристического числа: Числа . И вспомним определенние характаристического числа: Числа  , при которых однородное уравнение , при которых однородное уравнение 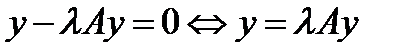 имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида  называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу  . .
Лемма Оператор A является симметричным, т.е.  – функций класса – функций класса 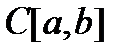 справедливо равенство справедливо равенство  . .
док: Рассмотрим выражение  : :  = = 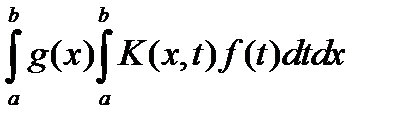 = =  = =  = =  = =  = = 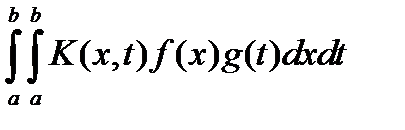 = =  = = 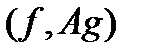 . .
28. Уравнение Фредгольма II-го рода с симметричным ядром. Действительность характеристических значений:
Рассмотрим уравнения Фредгольма II-го рода:  , (51) , (51)  (52). с непрерывным ядром (52). с непрерывным ядром  и непрерывной правой частью и непрерывной правой частью  . .
Опр: Ядро  интегрального оператора Фредгольма называется симметричным, если интегрального оператора Фредгольма называется симметричным, если 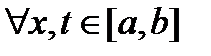 справедливо равенство: справедливо равенство:  . Обозначим интегральный оператор Фредгольма через A: . Обозначим интегральный оператор Фредгольма через A: 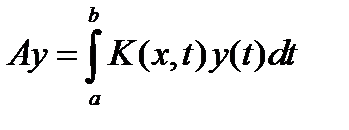 . И вспомним определенние характаристического числа: Числа . И вспомним определенние характаристического числа: Числа  , при которых однородное уравнение , при которых однородное уравнение 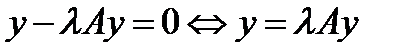 имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида  называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу  . .
Теорем а Все характеристические значения оператора Фредгольма с симметричным ядром действительны.
Док. Пусть  – характеристическое значение оператора Фредгольма A. Число – характеристическое значение оператора Фредгольма A. Число  можно не рассматривать, т.к. оно и так действительно. Тогда можно не рассматривать, т.к. оно и так действительно. Тогда  , , 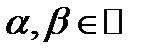 – характеристическое значение оператора Фредгольма A. Пусть – характеристическое значение оператора Фредгольма A. Пусть  – соответствующая собственная функция, т.е. решение однородного уравнения (52). Тогда – соответствующая собственная функция, т.е. решение однородного уравнения (52). Тогда  , что равносильно системе , что равносильно системе  , ,  = =  , ,  = =  = =  ,(равны между собой) откуда ,(равны между собой) откуда  , что означает, что , что означает, что  , а значит , а значит  .Приведём без доказательства ещё один факт. .Приведём без доказательства ещё один факт.
Теорема 2. 12. Оператор Фредгольма с симметричным ядром (отличным от тождественного нуля) имеет по крайней мере одно характеристическое число, не равное нулю.
29. Уравнение Фредгольма II-го рода с вырожденным ядром. Эквивалентность СЛАУ. Следствия
Рассмотрим уравнения Фредгольма II-го рода:  , (37) , (37)  (38). с непрерывным ядром (38). с непрерывным ядром  . .
опр: Ядро  называется вырожденным, если оно представимо в виде конечной суммы произведений функций, зависящих только от x, на функции, зависящих только от t: называется вырожденным, если оно представимо в виде конечной суммы произведений функций, зависящих только от x, на функции, зависящих только от t: 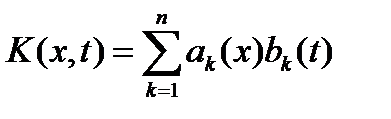 (39). (39).
Лемма об эквивалентности: Пусть 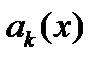 , ,  , ,  . Тогда уравнение Фредгольма II-го рода (37) эквивалентно СЛАУ (41) с коэффициентами (42), т.е. имеют место следующие утверждения: . Тогда уравнение Фредгольма II-го рода (37) эквивалентно СЛАУ (41) с коэффициентами (42), т.е. имеют место следующие утверждения:
1) Всякое решение  уравнения (37) представимо в виде уравнения (37) представимо в виде  (40), где (40), где 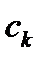 является решением СЛАУ: является решением СЛАУ:  (41). где коэффициенты (41). где коэффициенты  и и 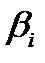 вычисляются по формулам: вычисляются по формулам:  , ,  (42). (42).
2) Наоборот, всякому решению 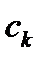 СЛАУ (41) с коэффициентами (42) соответствует решение СЛАУ (41) с коэффициентами (42) соответствует решение  уравнения (37) вида (40). уравнения (37) вида (40).
док: Перенесём интегральное слагаемое в уравнении  в правую часть: в правую часть:  и учтем вид вырожденного ядра: и учтем вид вырожденного ядра:  = = 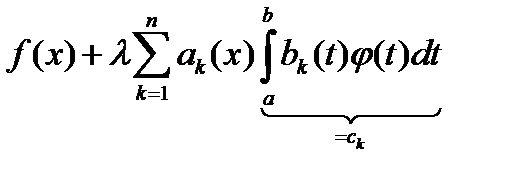 . Таким образом равенство (40) получено. Чтобы найти числа . Таким образом равенство (40) получено. Чтобы найти числа 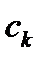 , поменяем в нём x на t, а индекс суммирования k на j и подставим его в каждое из равенств: , поменяем в нём x на t, а индекс суммирования k на j и подставим его в каждое из равенств:  , получим , получим  = = 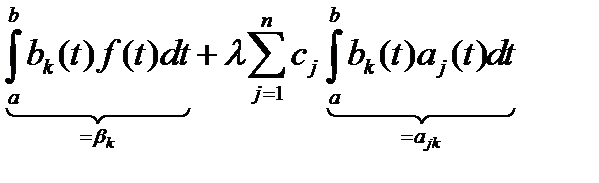 или короче или короче 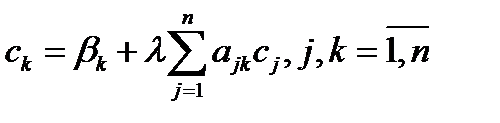 .Записав последнее равенство в матричном виде, получим (41). Теперь обратим внимание, что проведённые выкладки означают, что если .Записав последнее равенство в матричном виде, получим (41). Теперь обратим внимание, что проведённые выкладки означают, что если  – решение (37), то его можно записать в виде (40), причём где – решение (37), то его можно записать в виде (40), причём где 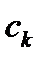 являются решением СЛАУ (41) с коэффициентами (42). Иначе говоря, выполняется утверждение 1) леммы. С другой стороны, вычислив по заданному ядру являются решением СЛАУ (41) с коэффициентами (42). Иначе говоря, выполняется утверждение 1) леммы. С другой стороны, вычислив по заданному ядру 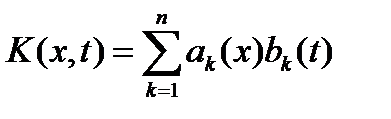 коэффициенты (42), мы можем обратить все выкладки и прийти к выводу, что функция коэффициенты (42), мы можем обратить все выкладки и прийти к выводу, что функция  , вычисленная о формуле (40), обязана удовлетворять , вычисленная о формуле (40), обязана удовлетворять
уравнению (37). Иными словами, выполняется утверждение 2) леммы
Следствия: (Альтернатива Фредгольма). Пусть 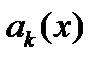 , ,  , ,  , а , а 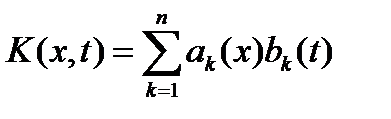 -вырожденное ядро. Тогда -вырожденное ядро. Тогда  имеет только тривиальное решение имеет только тривиальное решение 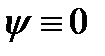 .Суть данной теоремы в том, что существование единственного решения (37) равносильно отличию от нуля определителя матрицы в (41). Следующая теорема относится к случаю, когда этот определитель равен нулю. .Суть данной теоремы в том, что существование единственного решения (37) равносильно отличию от нуля определителя матрицы в (41). Следующая теорема относится к случаю, когда этот определитель равен нулю.
Теорема Пусть 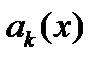 , ,  , ,  , а , а 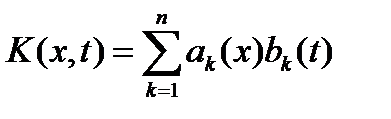 - вырожденное ядро. Кроме того - вырожденное ядро. Кроме того  - ФСР однородного уравнения(38). Тогда уравнение (37) либо имеет бесконечно много решений - ФСР однородного уравнения(38). Тогда уравнение (37) либо имеет бесконечно много решений  реализуется, если функция f(x) ортогональна в смысле скалярного произведения реализуется, если функция f(x) ортогональна в смысле скалярного произведения  всем решениям сопряжённого однородного уравнения всем решениям сопряжённого однородного уравнения  Если же для какого-либо решения Если же для какого-либо решения  этого уравнения этого уравнения  уравнение (37) не имеет решений вообще уравнение (37) не имеет решений вообще
|



 ,
,  . с непрерывным ядром
. с непрерывным ядром  и непрерывной правой частью
и непрерывной правой частью  .
.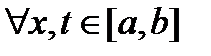 справедливо равенство:
справедливо равенство:  . Обозначим интегральный оператор Фредгольма через A:
. Обозначим интегральный оператор Фредгольма через A: 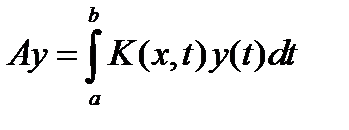 . И вспомним определенние характаристического числа: Числа
. И вспомним определенние характаристического числа: Числа  , при которых однородное уравнение
, при которых однородное уравнение 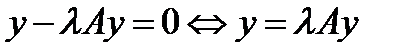 имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида
имеет нетривиальное решение, называются характеристическими числами оператора A, а всё множество таких чисел вида  называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу
называется спектром оператора A. Само же нетривиальное решение y называется собственной функцией оператора A, соответствующей характеристическому числу  .
. и
и  ,
,  – заданные функции, и однородная задача:
– заданные функции, и однородная задача:  (59),
(59),  (60),
(60),  (61) не имеет других решений, кроме тождественного нуля. Тогда задача Штурма–Лиувилля:
(61) не имеет других решений, кроме тождественного нуля. Тогда задача Штурма–Лиувилля:  ,
,  (63), где
(63), где  функция Грина задачи (59) – (61), а
функция Грина задачи (59) – (61), а  т.е. y(x) является собственной функцией задачи (62), (60), (61), соответствующей собственному значению
т.е. y(x) является собственной функцией задачи (62), (60), (61), соответствующей собственному значению  рассматривать как известную функцию, представляется в виде:
рассматривать как известную функцию, представляется в виде: 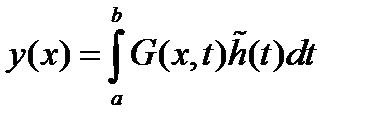 (64), откуда
(64), откуда  =
=  . Итак, пара
. Итак, пара  есть собственная функция задачи (62), (60), (61) и соответствующее ему собственное значение тогда и только тогда, когда пара
есть собственная функция задачи (62), (60), (61) и соответствующее ему собственное значение тогда и только тогда, когда пара  – функций класса
– функций класса 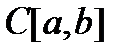 справедливо равенство
справедливо равенство  .
. :
:  =
= 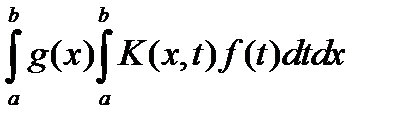 =
=  =
=  =
=  =
=  =
= 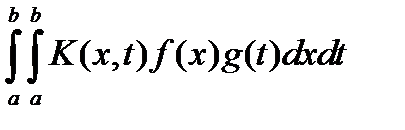 =
=  =
= 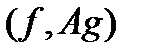 .
. – характеристическое значение оператора Фредгольма A. Число
– характеристическое значение оператора Фредгольма A. Число  можно не рассматривать, т.к. оно и так действительно. Тогда
можно не рассматривать, т.к. оно и так действительно. Тогда  ,
, 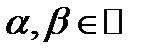 – характеристическое значение оператора Фредгольма A. Пусть
– характеристическое значение оператора Фредгольма A. Пусть  – соответствующая собственная функция, т.е. решение однородного уравнения (52). Тогда
– соответствующая собственная функция, т.е. решение однородного уравнения (52). Тогда  , что равносильно системе
, что равносильно системе  ,
,  =
=  ,
,  =
=  =
=  ,(равны между собой) откуда
,(равны между собой) откуда  , что означает, что
, что означает, что  , а значит
, а значит  .Приведём без доказательства ещё один факт.
.Приведём без доказательства ещё один факт. .
. называется вырожденным, если оно представимо в виде конечной суммы произведений функций, зависящих только от x, на функции, зависящих только от t:
называется вырожденным, если оно представимо в виде конечной суммы произведений функций, зависящих только от x, на функции, зависящих только от t: 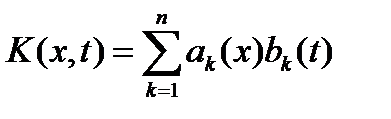 (39).
(39).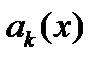 ,
,  ,
,  . Тогда уравнение Фредгольма II-го рода (37) эквивалентно СЛАУ (41) с коэффициентами (42), т.е. имеют место следующие утверждения:
. Тогда уравнение Фредгольма II-го рода (37) эквивалентно СЛАУ (41) с коэффициентами (42), т.е. имеют место следующие утверждения: уравнения (37) представимо в виде
уравнения (37) представимо в виде  (40), где
(40), где 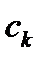 является решением СЛАУ:
является решением СЛАУ:  (41). где коэффициенты
(41). где коэффициенты  и
и 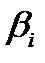 вычисляются по формулам:
вычисляются по формулам:  ,
,  (42).
(42). и учтем вид вырожденного ядра:
и учтем вид вырожденного ядра:  =
= 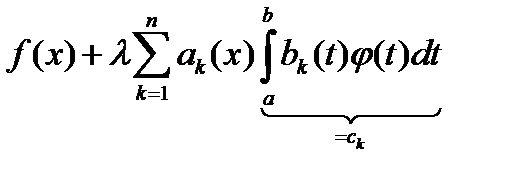 . Таким образом равенство (40) получено. Чтобы найти числа
. Таким образом равенство (40) получено. Чтобы найти числа  , получим
, получим  =
= 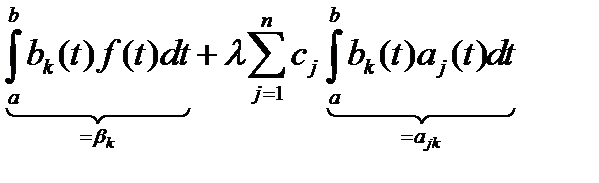 или короче
или короче 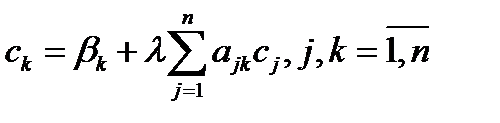 .Записав последнее равенство в матричном виде, получим (41). Теперь обратим внимание, что проведённые выкладки означают, что если
.Записав последнее равенство в матричном виде, получим (41). Теперь обратим внимание, что проведённые выкладки означают, что если  имеет только тривиальное решение
имеет только тривиальное решение 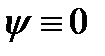 .Суть данной теоремы в том, что существование единственного решения (37) равносильно отличию от нуля определителя матрицы в (41). Следующая теорема относится к случаю, когда этот определитель равен нулю.
.Суть данной теоремы в том, что существование единственного решения (37) равносильно отличию от нуля определителя матрицы в (41). Следующая теорема относится к случаю, когда этот определитель равен нулю. - ФСР однородного уравнения(38). Тогда уравнение (37) либо имеет бесконечно много решений
- ФСР однородного уравнения(38). Тогда уравнение (37) либо имеет бесконечно много решений  реализуется, если функция f(x) ортогональна в смысле скалярного произведения
реализуется, если функция f(x) ортогональна в смысле скалярного произведения  всем решениям сопряжённого однородного уравнения
всем решениям сопряжённого однородного уравнения  Если же для какого-либо решения
Если же для какого-либо решения  этого уравнения
этого уравнения  уравнение (37) не имеет решений вообще
уравнение (37) не имеет решений вообще


