
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действительность собственных значений оператора ШЛСтр 1 из 3Следующая ⇒
Действительность собственных значений оператора ШЛ Все собственные значения задачи Штурма–Лиувилля действительны. Док: Пусть
Ортогональность собственных функций оператора ШЛ. Пусть Штурма–Лиувилля, соответствующие разным собственным значениям
Тогда
док: Напомним, что все линейно независимые собственные функции задачи Штурма–Лиувилля могут быть выражены через действительнозначные собственные функции, и мы для удобства ими и ограничиваемся. Пусть
Отсюда
Простота собственных значений оператора ШЛ Пусть Штурма–Лиувилля, соответствующие одному и тому же значению Док: Лемма билета 2 утвержает
Как известно из общей теории линейных ОДУ n-го порядка, если определитель Вронского системы решений одного и того же линейного уравнения равен нулю хотя бы в одной точке, то он равен нулю на всём промежутке, на котором выполняется уравнение (в нашем случае это Замечание Доказанное свойство называется простотой собственных значений задачи Штурма–Лиувилля и означает, что кратность каждого собственного значения равна 1.
Теорема Стеклова. Пример: разложить функцию в ряд по собственным функциям задачи ШЛ. Пусть Пусть собственных функций задачи Штурма–Лиувилля:
Тогда справедливо представление функции f(x) в виде ряда (Фурье):
Пример: Пусть дана задача ШЛ:
Тогда, решив её как мы сделали в примере 1. 3 (с. 6), получим систему собственных функций:
Посчитав норму собственных функций:
получим представление для f(x): что совпадает с формулой разложения f(x) в тригонометрический ряд Фурье по косинусам. Для получим
Действительность собственных функций оператора ШЛ. Без ограничения общности можно считать, что все собственные функции задачи Штурма–Лиувилля действительнозначны. Док: Пусть функция y(x) = u(x) + iv(x) – комплекснозначная собственная функция задачи Штурма–Лиувилля, соответствующая собственному значению можно переписать в виде: Поскольку
Это означает, что функции u(x) и v(x) также являются собственными функциями, соответствующими одному и тому же собственному значению По теореме билета 5 о линейной зависимости функций, соответствующие одному и тому же значению
Таким образом, введение комплекснозначных собственных функций не обо- гащает систему всех собственных функций задачи Штурма–Лиувилля, а лишь добавляет в неё линейно зависимые элементы.
Лемма о диссипативности Пусть f(x) – функция класса Тогда справедливо неравенство: док: Проверим неравенства: Обоснуем первое неравенство. Рассмотрим три случая: 1) 2) 3) Второе доказывается аналогично
Предел последовательности собственных значений Собственные значения задачи Штурма–Лиувилля образуют бесконечное множество, его можно пронумеровать в порядке возрастания, и полученная последовательность
Теорема о сущ шаг 2
Определим
Проверим теперь выполнение условий 1)-4) 1)
при
2) при любом фиксированном 3) при любом фиксированном Для того, чтобы убедиться в справедливости этого равенства для по- строенной
откуда 4) при любом фиксированном При этом при построении функции чтобы при – как они удовлетворяли КУ, – получается, что
Теорема Гильберта Пусть
При этом справедлива формула: док: Существование решения Пользуясь явным видом
Убедимся, что
Откуда Единственность: Пусть
Замечание 1. 1. Из теоремы 1. 1 и теоремы 1. 3 моментально следует, что при выполнении условий решение.
Действительность собственных значений оператора ШЛ Все собственные значения задачи Штурма–Лиувилля действительны. Док: Пусть
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.055 с.) |
 – собственное значение задачи Штурма–Лиувилля и, соответственно, оператора Штурма–Лиувилля L[y]. Пусть y(x) = u(x)+iv(x)
– собственное значение задачи Штурма–Лиувилля и, соответственно, оператора Штурма–Лиувилля L[y]. Пусть y(x) = u(x)+iv(x)  – соответствующая собственная функция. Тогда
– соответствующая собственная функция. Тогда  , что равносильно системе
, что равносильно системе =>
=>  равны между собой
равны между собой , что означает, что
, что означает, что  , а значит
, а значит 
 и
и  – собственные функции задачи
– собственные функции задачи , соответственно:
, соответственно: 


 =
=  =
=  =[ в силу симметричности L]=
=[ в силу симметричности L]=  =
=  =
= 
 тогда
тогда 
 , тогда
, тогда 
 – функции класса
– функции класса  т.е. удовлетворяющих классическим краевым условиям на концах
т.е. удовлетворяющих классическим краевым условиям на концах  и
и  , где
, где 
 и удовлетворяет КУ:
и удовлетворяет КУ:  ,
, 
 – ортогональная система всех линейно независимых
– ортогональная система всех линейно независимых
 ,
,  , причем ряд сходится абсолютно и равномерно на всем
, причем ряд сходится абсолютно и равномерно на всем 
 ,
,  ,
,  ,
, 
 ,
, 
 ,
, 
 тригонометрический ряд Фурье по синусам:
тригонометрический ряд Фурье по синусам: ,
,  .
. . Тогда равенство:
. Тогда равенство: 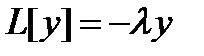

 в силу теоремы билета 3, а
в силу теоремы билета 3, а  в силу определения основного дифференциального оператора билета 2. Данное уравнения распадается на два, для
в силу определения основного дифференциального оператора билета 2. Данное уравнения распадается на два, для  и
и 
 ,
,  .
. .
. такое что:
такое что: , откуда сразу
, откуда сразу  , либо
, либо , откуда сразу
, откуда сразу  .
. (т.е. удовлетворяет классическим КУ).
(т.е. удовлетворяет классическим КУ).
 ,
, 
 . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство: 
 . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство:  . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство: 
 :
:
 -вронскиан пары функций
-вронскиан пары функций  .
.
 , где
, где  ;
;  и не обращается в нуль, так как
и не обращается в нуль, так как а Вронскиан системы линейно независимых решений однородного линейного уравнения всюду отличен от нуля. Числитель же непрерывен и даже дважды непрерывно дифференцируем в
а Вронскиан системы линейно независимых решений однородного линейного уравнения всюду отличен от нуля. Числитель же непрерывен и даже дважды непрерывно дифференцируем в  . Однако при
. Однако при  и
и у него один и тот же предел:
у него один и тот же предел:

 и удовлетворяет однородному уравнению (1):
и удовлетворяет однородному уравнению (1):  при
при 
 и
и  как решения однородного уравнения, а все остальные множители от x вообще не зависят.
как решения однородного уравнения, а все остальные множители от x вообще не зависят.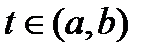 первая производная
первая производная  имеет в точке
имеет в точке  разрыв первого рода, причём:
разрыв первого рода, причём: 
 , найдём
, найдём ,
,

 удовлетворяет краевым условиям по x:
удовлетворяет краевым условиям по x:  ,
, 
 мы позаботились о том,
мы позаботились о том, она вела себя как
она вела себя как  , а при
, а при 
 . Поскольку мы строили
. Поскольку мы строили  и
и  так, чтобы
так, чтобы

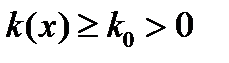 и
и  – заданные функции,
– заданные функции,  ,
,  , и однородная (т.е. при
, и однородная (т.е. при  ) задача (1) –(3) не имеет других решений, кроме тождественного нуля. Тогда для любой функций
) задача (1) –(3) не имеет других решений, кроме тождественного нуля. Тогда для любой функций  существует и притом единственное решение краевой задачи (1) – (3):
существует и притом единственное решение краевой задачи (1) – (3): (1)
(1) (2)
(2) (3)
(3) , где
, где  -функция Грина задачи (1)-(3)
-функция Грина задачи (1)-(3) ,
,  . Запишем
. Запишем и тогда z(x) примет вид:
и тогда z(x) примет вид: =
=  =
=  +
+  =
=  +
+  =
=  +
+  . Тогда
. Тогда  =
=  +
+  +
+  -
-  =
=  +
+  .Тогда
.Тогда  =
=  +
+  +
+  -
-  =[подставим c(x)]=
=[подставим c(x)]=  =
= 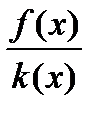 =
=  +
+  +
+  .
. +
+  -
-  =
=  +
+  +
+  +
+  +
+  -
-  +
+  +
+  +
+  .Проверим выполнение КУ на левом конце: При
.Проверим выполнение КУ на левом конце: При 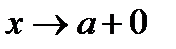
 ,
,
 .Краевое условие на правом конце проверяется аналогично. Существование решения, заданного равенством (6), доказано.
.Краевое условие на правом конце проверяется аналогично. Существование решения, заданного равенством (6), доказано. и
и  – два решения краевой задачи (1) – (3). Тогда их разность
– два решения краевой задачи (1) – (3). Тогда их разность  удовлетворяет однородной задаче:
удовлетворяет однородной задаче: Но по условию теориемы у такой задачи есть только тривиальное решение, те
Но по условию теориемы у такой задачи есть только тривиальное решение, те  , а значит
, а значит  .
.


