
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональность собственных функций оператора ШЛ.Содержание книги
Поиск на нашем сайте
Пусть Штурма–Лиувилля, соответствующие разным собственным значениям
Тогда
док: Напомним, что все линейно независимые собственные функции задачи Штурма–Лиувилля могут быть выражены через действительнозначные собственные функции, и мы для удобства ими и ограничиваемся. Пусть
Отсюда
Простота собственных значений оператора ШЛ Пусть Штурма–Лиувилля, соответствующие одному и тому же значению Док: Лемма билета 2 утвержает
Как известно из общей теории линейных ОДУ n-го порядка, если определитель Вронского системы решений одного и того же линейного уравнения равен нулю хотя бы в одной точке, то он равен нулю на всём промежутке, на котором выполняется уравнение (в нашем случае это Замечание Доказанное свойство называется простотой собственных значений задачи Штурма–Лиувилля и означает, что кратность каждого собственного значения равна 1.
Теорема Стеклова. Пример: разложить функцию в ряд по собственным функциям задачи ШЛ. Пусть Пусть собственных функций задачи Штурма–Лиувилля:
Тогда справедливо представление функции f(x) в виде ряда (Фурье):
Пример: Пусть дана задача ШЛ:
Тогда, решив её как мы сделали в примере 1. 3 (с. 6), получим систему собственных функций:
Посчитав норму собственных функций:
получим представление для f(x): что совпадает с формулой разложения f(x) в тригонометрический ряд Фурье по косинусам. Для получим
Действительность собственных функций оператора ШЛ. Без ограничения общности можно считать, что все собственные функции задачи Штурма–Лиувилля действительнозначны. Док: Пусть функция y(x) = u(x) + iv(x) – комплекснозначная собственная функция задачи Штурма–Лиувилля, соответствующая собственному значению
можно переписать в виде: Поскольку
Это означает, что функции u(x) и v(x) также являются собственными функциями, соответствующими одному и тому же собственному значению По теореме билета 5 о линейной зависимости функций, соответствующие одному и тому же значению
Таким образом, введение комплекснозначных собственных функций не обо- гащает систему всех собственных функций задачи Штурма–Лиувилля, а лишь добавляет в неё линейно зависимые элементы.
Лемма о диссипативности Пусть f(x) – функция класса Тогда справедливо неравенство: док: Проверим неравенства: Обоснуем первое неравенство. Рассмотрим три случая: 1) 2) 3) Второе доказывается аналогично
Неотрицательность собственных значений оператора ШЛ. Предел последовательности собственных значений Пусть q(x) > m. Тогда для всех собственных значений
Док: Рассмотрим собственную функцию y(x):
В силу леммы о диссипативности слагаемое откуда оценка: Предел последовательности собственных значений Собственные значения задачи Штурма–Лиувилля образуют бесконечное множество, его можно пронумеровать в порядке возрастания, и полученная последовательность
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.30.216 (0.005 с.) |

 и
и  – собственные функции задачи
– собственные функции задачи , соответственно:
, соответственно: 


 =
=  =
=  =[ в силу симметричности L]=
=[ в силу симметричности L]=  =
=  =
= 
 тогда
тогда 
 , тогда
, тогда 
 – функции класса
– функции класса  т.е. удовлетворяющих классическим краевым условиям на концах
т.е. удовлетворяющих классическим краевым условиям на концах  и
и  , где
, где 
 и удовлетворяет КУ:
и удовлетворяет КУ:  ,
, 
 – ортогональная система всех линейно независимых
– ортогональная система всех линейно независимых
 ,
,  , причем ряд сходится абсолютно и равномерно на всем
, причем ряд сходится абсолютно и равномерно на всем 
 ,
,  ,
,  ,
, 
 ,
, 
 ,
, 
 тригонометрический ряд Фурье по синусам:
тригонометрический ряд Фурье по синусам: ,
,  .
. . Тогда равенство:
. Тогда равенство: 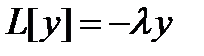

 в силу теоремы билета 3, а
в силу теоремы билета 3, а  в силу определения основного дифференциального оператора билета 2. Данное уравнения распадается на два, для
в силу определения основного дифференциального оператора билета 2. Данное уравнения распадается на два, для  и
и 
 ,
,  .
. .
. такое что:
такое что: , откуда сразу
, откуда сразу  , либо
, либо , откуда сразу
, откуда сразу  .
. (т.е. удовлетворяет классическим КУ).
(т.е. удовлетворяет классическим КУ).
 ,
, 
 . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство: 
 . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство:  . Тогда
. Тогда  , и неравенство превращается в равенство:
, и неравенство превращается в равенство: 
 задачи Штурма–Лиувилля:
задачи Штурма–Лиувилля: справедлива оценка
справедлива оценка 
 . Имеем:
. Имеем: =
=  =
=  +
+  +
+  +
+  +
+  .
. с другой стороны
с другой стороны  .
. .
. :
:



