
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт тарифов предпринимательских рисковСодержание книги
Поиск на нашем сайте
Виды предпринимательских рисков: · страхование убытков по единица продаж · депозитов · банков невозврата кредитов · остановок производства · инноваций – венчурного бизнеса · рисков снижения объемов продаж или увеличение расходов · страхование урожаев Все эти виды страхования страхуют потери, которые произошли не по вине страхователя. Страховщик имеет право контролировать прочес соблюдения технологий норм. На примере страхования урожаев X-сам урожай FК-функция распределения величины урожая.
В качестве ориентира вводится ф-я потерь. За ориентир принимается некоторая средняя
Fy=1-Fx dFy = - fFx
ML – средние потери EL –ожидаемые потери, они меньше чем средние EL=ML-pa Событие
Х Y 0
Ф-я потерь
1)
Таким образом EL=F
2)
dFy = -dFx
EL=E(Y|I)pa; E(Y|I)
Модель коллективного риска и стохастическое ур-ние динамики страховых резервов.
Составной Пуассоновский процесс N(t)
Zi = Ki Ii Si n – договоров EIi = p
Модель коллективного риска имеют следующие допущения: 1) процесс поступления рисков растянут во времени. У нее есть динамика, при это не рассматривается вероятность индивидуальных рисков (нет n и p). 2) Размеры выплат друг от друга не зависят 3) В страх. компанию поступает непрерывно во времени приток договоров с некоторой интенсивностью.
В этих моделях рассмотрим динамику резервов.
Задача: ставится задача исследовать вероятность разорения компании (резервы станут <0) в зависимости от стартового капитала и страховой премии, величины страхового тарифа.
Yt –диск переменная – стартовый капитал страховщика
с – страховая премия t – время N(t) – случайная величина, кол-во рисков
Z=
N=
Z=
Будем считать, что все Zn друг от друга не зависят и все они одинаковы.
Sn=1, Rn-одинаковые Zn=Rn
Z=
ER ED= EN DN=
Надо найти EZ, DZ
Если бы Z=NR, то как неоднородный портфель (???) EZ=
EZ=
=
=ER
EN
DZ =
E(ct)=EZ= C= Т Т0 Т+r
Если Y0<0, то
N(t) – представляет собой пуассоновский процесс P(N(t) = N(t)
T
T-время между событиями
Ezt=
Величину
Если y
В общем случае имеет место неравенство Крамера-Лундберга
Где R -положительный корень интегрального уравнения
x=0,1….
t
Так же потоки являются аппаратами массового обслуживания.
Простейший пуассоновский поток – процесс с независимыми приращениями Этот поток обладает св-ми 1)стационарность, т.е. вероятность появления х событий на интервале (t; t+ Зависит от
2) отсутствие последействия – предыстория не влияет на вероятности появления событий в будущем. Только начальное состояние влияет на будущее, прошлое не имеет значения, его нет.
3)ординарность, т.е. вероятность появления в некотором «малом» интервале времени более чем одного события почти равна 0. Эта вероятность на порядок меньше, чем вероятность вообще ни одного события или одного события.
Следствием из этих св-в является то, что интервалы времени между событиями распределены экспоненциально.
Проверка св-в
1)
Разложим е в ряд Тейлора и будем считать, что
А если
T=среднее время между отдельными событиями
Из проверки видно, что интервалы времени распределены по экспоненциальному закону.
Т.к
Это означает, что ф-я распределения
Кривая
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.191.148 (0.01 с.) |


 , f-франшиза,
, f-франшиза,  ,
, 
 величина обратная по отношения к ф-ции х
величина обратная по отношения к ф-ции х


 1 и 2 способ соответсвенно
1 и 2 способ соответсвенно




 нижний частный момент порядка 1, относительно
нижний частный момент порядка 1, относительно 
 ;
; 



 ML
ML

 у
у  + ct -
+ ct - 



 ; N=1,2,3……
; N=1,2,3……
 =
= 



 *
*  (???)
(???) ) * p(N=n)
) * p(N=n) =
= = ER EN
= ER EN

 интенсивность, скорость
интенсивность, скорость , тогда C=
, тогда C=  , С - страховая премия, тариф.
, С - страховая премия, тариф. )
)
 вероятность, величина разорения
вероятность, величина разорения
 e
e 

 -среднее время между 2 скачками
-среднее время между 2 скачками
 Z) = 1- e
Z) = 1- e  , то имеется решение:
, то имеется решение:


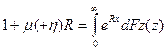

 генерирует поток событий
генерирует поток событий



 постоянна, потому поток стационарен
постоянна, потому поток стационарен - среднее время между события малость означает, что
- среднее время между события малость означает, что  T <<1
T <<1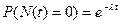


 , т.е
, т.е  -величина маленькая.
-величина маленькая.
 , то
, то 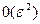 является величиной второго порядка малости.
является величиной второго порядка малости. означает, что интервал
означает, что интервал 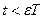

 от t не зависит, то можно положить, что t=0
от t не зависит, то можно положить, что t=0








