
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття системи одночасних структурних рівнянь та різновиди їх формСодержание книги
Поиск на нашем сайте
Поняття системи одночасних структурних рівнянь та різновиди їх форм В економіці існує багато задач, коли для опису економічного процесу доводиться використовувати систему взаємозв'язків між декількома показниками та факторами і які описуються системою рівнянь регресії. Наприклад, якщо Y1 - курс гривні до американського долара, Y2 - обсяг імпорту, Хі (і=1,2,..., m) - фактори, від яких залежать ці показники, наприклад: X1 - національний прибуток, Х2 - середній рівень заробітної плати, Х3 - обсяг імпорту, Х4 - ціни енергоносіїв, що купуються, Х5 - інфляція долара, Х6 - відсоткові ставки кредитів у банках, X7 - розмір емісії, Х8 - інфляція гривні за попередні періоди в Україні, Росії, Германії.
В розглянутому прикладі систему регресійних рівнянь можна записати у вигляді
При побудові моделей пояснювальні зміні можуть мати запізнення (лаги) за один, два або більше періодів. Наприклад, інфляція долара в Україні залежить від рівня його інфляції в Германії, Америці, Японії, Росії за попередній період.
Найчастіше системи одночасних структурних рівнянь включають лінійні рівняння. Нелінійність зв'язків зводиться до лінійних відносно змінних або апроксимується лінійними співвідношеннями. Динаміка економічних зв'язків враховується за допомогою часових лагів або лагових зміних.
В загальному вигляді економетрична модель на основі системи одночасних рівнянь має вигляд
В цій моделі окремі коефіцієнти можуть дорівнювати нулю, якщо відповідна зміна не входить до рівняння. Якщо деяке рівняння описує детерміновані співвідношення (вони не містять випадкових величин), то відповіднi відхилення еіt, також можуть дорівнювати нулю.
Систему (1) можна записати у матричній формі Yt = АYt + ВХt + Ut, (2) де Yt - вектор ендогених (залежних) змінних; Xt - матриця екзогених (незалежних) зміних, U - вектор відхилень, A - матриця коефіцієнтів при змінних Y розміром k х k; В - матриця коефіцієнтів при змінних X розміром k x m.
Економетрична модель вигляду (1) відображає структуру зв'язків між змінними величинами і називається структурною формою економетричної моделі. Використовуючи матричний запис (2) і припущення, що ранг системи дорівнює m, розв'яжемо цю систему відносно Y:
де П = (U - А)-1 вектор-стовпець, складений з лінійних комбінацій випадкових змінних Еt.
Рівняння (3) можна записати у вигляді системи
Це називається зведеною формою системи одночасних рівнянь.
Система одночасних структурних рівнянь називається рекурсивною формою системи, якщо матриця А параметрів ендогенних змінних структурної системи (1) має трикутний вигляд, а випадкові відхилення не корелюють між собою. Складові систем рівнянь При дослідженні систем одночасних рівнянь змінні діляться на два великі класи - ендогенні й екзогенні змінні. Ендогенні змінні - це змінні, значення яких визначаються всередині моделі. Екзогенні змінні - це зовнішні щодо моделі змінні. Їхні значення визначаються поза моделлю і тому вони вважаються фіксованими. Така класифікація змінних дозволяє вказати методи визначення ендогенних змінних. Наприклад, у системі (1) функції попиту та пропозиції, умова рівноваги визначають величини попиту qtD пропозиції qt S і ціну Р. Всі ці змінні є ендогенними, тому що вони визначаються усередині системи. У моделі (3) змінні С і Y є ендогенними змінними, які оцінюються усередині моделі. Змінна I задається (визначається) поза моделлю. Отже, вона є екзогенною змінною. Зі співвідношення (З) видно, що змінна С залежить від Y і від ε, зі співвідношення (З2) - Y залежить від С и від I. Неважко помітити, що обидві змінні С и Y можуть бути виражені через І і ε. Підставивши ct із другого співвідношення в перше, маємо: yt = Коефіцієнт Рівняння, що становлять вихідну модель, називають структурними рівняннями моделі. Їх підрозділяють на поведінкові рівняння й рівняння-тотожності. У перших з них описуються взаємодії між змінними. У других - співвідношення, які мають виконуватися у всіх випадках (помітимо, що тотожності не містять оцінцені параметри й випадкові складовіі). Наприклад, у моделі (3) рівняння (31) - поведінкове, а (32) - тотожність. Рівняння, які відображають схему визначення ендогенних змінних, називаються рівняннями у наведеній формі (наведеними рівняннями): ендогенні змінні виражені тільки через екзогенні або визначені заздалегідь змінні, а також випадкові складовіі. Прикладами таких рівнянь є рівняння (81) і (82). Визначеними заздалегідь змінними називаються лагові ендогенні змінні, значення яких визначені до розгляду співвідношень. Наприклад, рівняння попиту в моделі «попит - пропозиція» матиме вигляд qt S = α0 + α1 іt + α2 рt -1 + εt, (9)
Тут змінна pt -1 – це ціна товару в попередній момент часу; pt+1 - визначена заздалегідь змінна. 3. МНК для систем одночасних рівнянь - непрямий метод найменших квадратів(НМНК). Безпосереднє використання МНК для оцінки параметрів кожного з рівнянь регресії, що входять до системи одночасних рівнянь, у більшості випадків приводить до незадовільного результату: оцінки виходять зміщені й неспроможними, а статистичні висновки за ними - некоректними. Один з таких можливих методів - непрямий метод найменших квадратів (НМНК), заснований на використанні наведених рівнянь. Для ілюстрації КМНК розглянемо модель Кейнса формування доходів (3). У наведеному виді ця модель виражається через систему (8). Покладемо в (81) Покладемо в (82) Тоді замість (81) і (82) маємо: yt = λ10 + λ11 · іt + vt, (91) ct = λ 20 + λ21· іt + vt. (92) Тому що обсяг інвестицій I є екзогенною змінною моделі, то іt некорелює із випадковим членом εt в рівняннях (81), (82), а отже, і з vt в (91) і (92). Це означає, що для випадкового члена vt виконуються передумови МНК. Тому оцінки λ*10 , λ*11, λ*20 , λ*21, отримані за МНК, будуть значущими оцінками параметрів λ10 , λ11, λ20 , λ21. Знаючи отримані оцінки, нескладно визначити оцінки b0 і b1 коефіцієнтів β0 і β1 рівняння ct = β0 + β1 уt + εt (З1): b1 = β1 * = Визначення оцінок за зазначеною схемою називається непрямим методом найменших квадратів (НМНК). Оцінки b0 і b1, отримані за НМНК, є спроможними, а отже, при більших вибірках велика ймовірність, що вони будуть близькі до істинних значень параметрів. Таким чином, НМНК складається із наступних етапів: 1. Виходячи із структурних рівнянь, будуються рівняння у наведеній формі. 2. Оцінюються за МНК параметри рівнянь у наведеній формі. 3. На підставі оцінок, знайдених на етапі 2, оцінюються параметри структурних рівнянь.
Оцінка моделей із лагами Моделі із розподіленими лагами залежать від кількості (скінченної або нескінченної) лагів:
- Коефіцієнт - Сума всіх коефіцієнтів - Довільна сума
Модель зі скінченним лагом зводиться до рівняння множинної регресії:
Модель із нескінченної кількістю лагів перетворенням Койка зводиться до авторегресійної моделі (умова: коефіцієнти Перетворення Койка
де Це перетворення знімає проблему мультиколінеарності і дозволяє аналізувати короткотермінові і довготермінові властивості змінних: - у коротко термінованому періоді значення
- у довго терміновому періоді
- крім того як сума нескінченно спадної геометричної прогресії - при Але: серед пояснюючих змінних є змінна Структура часових рядів Систематична складова ч. р. – результат впливу постійно діючих складових: - тренд – системна лінійна або нелінійна компонента, яка змінюється у часі; - сезонність – період коливання спостережень ч. р. протягом одного року; - циклічність – період коливання за період більше 1 року. Стохастична (випадкова) складова – випадкова похибка (шум), яка впливає на часовий ряд нерегулярно, яка може з’явитися в разі різкого і раптового впливу (катастрофічні коливання) і мають найбільш сильний вплив на основні тенденції ч. р., і шум, викликаний діями наявних факторів або пов'язаний із похибками спостережень. Окрема складова ч. р. є функцією багатьох змінних: адитивна модель часового ряду мультиплікативна модель мішана модель Виявлення тренду: Один із найпростіших критеріїв – медіанний критерій: - часовий ряд обсягом - визначається медіана ряду - порівняння початкових значень із медіаною
- перевірка гіпотези про відсутність тренду: відхиляється за умов невиконання хоча б однієї нерівності Стаціонарні ряди Детерміновані ч. р. – значення спостережень ч. р. точно визначаються деякою математичною функцією, а сама функція є реалізацією досліджуваного процесу. Випадкові ч. р. – спостереження ч. р. описуються за допомогою функції розподілу ймовірностей. Стохастичний (випадковий) процес – процес, який розвивається на підставі законів теорії ймовірностей. Стаціонарний процес – основні властивості є незмінними у часі: - - - автоковаріація (коваріація між значеннями - сталий коефіцієнт автокореляції «Білий шум» - випадкова послідовність значень Поняття системи одночасних структурних рівнянь та різновиди їх форм
В економіці існує багато задач, коли для опису економічного процесу доводиться використовувати систему взаємозв'язків між декількома показниками та факторами і які описуються системою рівнянь регресії. Наприклад, якщо Y1 - курс гривні до американського долара, Y2 - обсяг імпорту, Хі (і=1,2,..., m) - фактори, від яких залежать ці показники, наприклад: X1 - національний прибуток, Х2 - середній рівень заробітної плати, Х3 - обсяг імпорту, Х4 - ціни енергоносіїв, що купуються, Х5 - інфляція долара, Х6 - відсоткові ставки кредитів у банках, X7 - розмір емісії, Х8 - інфляція гривні за попередні періоди в Україні, Росії, Германії.
В розглянутому прикладі систему регресійних рівнянь можна записати у вигляді
При побудові моделей пояснювальні зміні можуть мати запізнення (лаги) за один, два або більше періодів. Наприклад, інфляція долара в Україні залежить від рівня його інфляції в Германії, Америці, Японії, Росії за попередній період.
Найчастіше системи одночасних структурних рівнянь включають лінійні рівняння. Нелінійність зв'язків зводиться до лінійних відносно змінних або апроксимується лінійними співвідношеннями. Динаміка економічних зв'язків враховується за допомогою часових лагів або лагових зміних.
В загальному вигляді економетрична модель на основі системи одночасних рівнянь має вигляд
В цій моделі окремі коефіцієнти можуть дорівнювати нулю, якщо відповідна зміна не входить до рівняння. Якщо деяке рівняння описує детерміновані співвідношення (вони не містять випадкових величин), то відповіднi відхилення еіt, також можуть дорівнювати нулю.
Систему (1) можна записати у матричній формі Yt = АYt + ВХt + Ut, (2) де Yt - вектор ендогених (залежних) змінних; Xt - матриця екзогених (незалежних) зміних, U - вектор відхилень, A - матриця коефіцієнтів при змінних Y розміром k х k; В - матриця коефіцієнтів при змінних X розміром k x m.
Економетрична модель вигляду (1) відображає структуру зв'язків між змінними величинами і називається структурною формою економетричної моделі. Використовуючи матричний запис (2) і припущення, що ранг системи дорівнює m, розв'яжемо цю систему відносно Y:
де П = (U - А)-1 вектор-стовпець, складений з лінійних комбінацій випадкових змінних Еt.
Рівняння (3) можна записати у вигляді системи
Це називається зведеною формою системи одночасних рівнянь.
Система одночасних структурних рівнянь називається рекурсивною формою системи, якщо матриця А параметрів ендогенних змінних структурної системи (1) має трикутний вигляд, а випадкові відхилення не корелюють між собою.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.97.131 (0.012 с.) |


 (1)
(1) (3)
(3)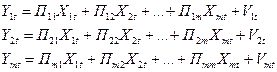 (4)
(4) (81 ) сt =
(81 ) сt =  (82 )
(82 ) в (81) представляє грошовий мультиплікатор, що визначає, на яку величину збільшується сукупний дохід при збільшенні обсягу інвестицій на одиницю.
в (81) представляє грошовий мультиплікатор, що визначає, на яку величину збільшується сукупний дохід при збільшенні обсягу інвестицій на одиницю. ,
, 
 ,
,  ,
,  ≈
≈ 
 b0 = β0 * =
b0 = β0 * = 


 – коротко терміновий мультиплікатор, характеризує зміну середнього значення Y під впливом одиничної зміни фактору Х в той же момент часу.
– коротко терміновий мультиплікатор, характеризує зміну середнього значення Y під впливом одиничної зміни фактору Х в той же момент часу. – довго терміновий мультиплікатор – характеризує зміну Y під впливом одиничної зміни фактору Х в кожному із часових періодів.
– довго терміновий мультиплікатор – характеризує зміну Y під впливом одиничної зміни фактору Х в кожному із часових періодів. – проміжний мультиплікатор.
– проміжний мультиплікатор.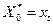 ;
;  ; …;
; …; 

 для лагових змінних є членами спадної геометричної прогресії:
для лагових змінних є членами спадної геометричної прогресії:  ,
,  - швидкість спадання коефіцієнтів зі збільшенням лагу):
- швидкість спадання коефіцієнтів зі збільшенням лагу):  .
.


 - ковзка середня між
- ковзка середня між  .
. розглядається як фіксоване і короткотерміновий мультиплікатор =
розглядається як фіксоване і короткотерміновий мультиплікатор = 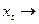 до деякого свого рівнозваженого значення
до деякого свого рівнозваженого значення  , то значення
, то значення  і
і 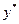 :
:

 ;
; є довготерміновим мультиплікатором;
є довготерміновим мультиплікатором; довготерміновий вплив буде сильнішим за короткотерміновий
довготерміновий вплив буде сильнішим за короткотерміновий 
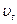 .
. , де Т - тренд, S – сезонність, С – циклічність, Е – випадковий шум:
, де Т - тренд, S – сезонність, С – циклічність, Е – випадковий шум:


 впорядковується за зростанням;
впорядковується за зростанням;


 - загальна кільсть серій знаків «+», «-»;
- загальна кільсть серій знаків «+», «-»;  - кількість найдовшої серії знаків.
- кількість найдовшої серії знаків.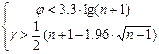


 ) залежить від величини лагу
) залежить від величини лагу 

 , якщо її математичне сподівання
, якщо її математичне сподівання  , а її елементи є некорельованими зі сталою дисперсією.
, а її елементи є некорельованими зі сталою дисперсією.


