
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графика с выводом результатаСодержание книги
Поиск на нашем сайте
расчета.............................................................................................. 22 4.1. Вывод промежуточных значений............................................. 22 4.2. Вывод графика временной функции......................................... 23 ЗАКЛЮЧЕНИЕ.................................................................................... 24 СПИСОК ИСПОЛЬЗОВАНЫХ ИСТОЧНИКОВ........................... 25 ПРИЛОЖЕНИЕ А. Листинг программы.............................. 2
Введение
С развитием промышленности возникает необходимость в автоматизации технологических процессов и производств. На данном этапе развития техники широкое применение находят роботы и робототехнические системы. Для управления производственными процессами в 70-е, 80-е годы стало возможным применение микропроцессорной техники. Развитие различных языков программирования (Fortran, Basic, Assembler, Pascal, C и т.д.) дает возможность разработки и внедрения объемных пакетов прикладных программ для управления сложными технологическими процессами и производствами. Пакеты прикладных программ дают возможность дистанционного управления и контроля сложных процессов с невозможным прямым вмешательством человека. Управляющая система намного быстрее и точнее выполняет поставленные задачи, не требуя при этом времени на отдых. Применение программного управления значительно увеличивает производительность труда. Первоначальные затраты материальных средств на установку и наладку микропроцессорного оборудования в процессе работы быстро окупаются. Это делает выгодным применение систем такого рода в производстве. Для написания программного обеспечения к микропроцессорному оборудованию подходит язык программирования Basic. Программы, написанные на нём, обладают высокой работоспособностью и не требуют от управляющей машины высоких аппаратных качеств. Они позволяют провести расчет параметров системы, как в машинном, так и в реальном времени.
Выбор и обоснование методов решения Понятие машинного и реального времени
Реализацию любой программы можно проводить по двум путям: либо в темпе быстродействия ЭВМ (с учётом быстродействия языка программирования), либо в реальном масштабе времени. При этом время задержки напрямую зависит от частоты процессора, и эта программа может наиболее объективно использоваться на той ЭВМ, для которой она была написана. Машинное время является относительным, т.к. зависит от быстродействия ЭВМ, от используемого языка, от сложности алгоритма и т.д.
Исследователь должен уметь связывать последовательность результатов с реальным временем, проводить эксперимент в реальном времени. Моделирование в реальном времени дает возможность оценивать эффективность алгоритмов для работы в реальных системах. Дискретизация времени
При исследовании блоков и систем во временной области на ЭВМ, в частности микроЭВМ, непрерывные процессы заменяются на дискретные. При этом временной интервал L представляется как совокупность дискретных интервалов:
где Tk – период квантования по времени непрерывной функции; n – количество шагов или квантов. Количество квантов выбирается не произвольно, а исходя из максимальной частоты процесса и допустимой погрешности при моделировании.
Реализация временных задержек в программе Можно выделить два основных способа реализации временных задержек в программе. Первый – самый простой – состоит в том, чтобы прямо указать программе, сделать паузу (например, оператором DELAY). Второй способ – организовать цикл, внутри которого выполняется арифметическая операция, абсолютно не влияющая на результат выполнения программы. Метод Крамера для решения системы линейных уравнений Система линейных уравнений:
a1x + b1x2= c1 a2x + b2x2 = c2,
Имеет одно решение (x1, x2), если система является невырожденной т.е. выполняется неравенство: a1b2-a2b1≠0,
Тогда решение можно найти по общим формулам:
Метод Ньютона
Задано: Введем обозначения: Так как вычисления искомого значения Итак, алгоритм решения: 1. Задаем значение 2. Вычисляется 3. Вычисляется 4. Определяется 5. Вычисляется
6. Проверяется условие Если условие выполняется, то 1.6. Алгоритм (схема) Горнера
Известно, что полином в общем виде записывается следующим образом:
Горнер предложил переиндексировать коэффициенты многочлена: Далее он предложил разложить многочлен и представить в виде:
Исходя из такого представления, он предложил алгоритм, который еще называют схемой Горнера: -все коэффициенты -должны учитываться все коэффициенты. Если они отсутствуют в полиноме, то их надо все равно использовать, считая их равными нулю; -до цикла FOR-NEXT взять значения y=A(1); -цикл по управляющей переменной организовывать с I=2 до X+1; -в цикле использовать формулу: Y=Y*X+A(I). Если все значения Y надо сохранить, то Y следует организовать тоже как массив. Построение графика
Что касается построения графиков функций, то можно использовать графические операторы PSET и LINE. Однако при построении графиков необходимо всегда решать вопрос, связанный с масштабированием графиков. Во-первых, при построении графиков на компьютере пользователь всегда имеет дело с дискретными функциями: yn = f(ndx) или yn = f(nTk), где dx – шаг изменения аргумента; Tk – период квантования, который является тоже шагом по аргументу, которым является время t = nTk. Необходимо всегда оценивать минимальное и максимальное значение функции: y0(min) при n=0 и yn(max) при nmax. Кроме того, необходимо выбрать начальную точку (a, b) для построения графика, определить границы окончания графика справа и сверху, а потом рассчитать масштаб по аргументу и по функции. Для пояснения на рисунке 1.1 показан произвольный график:
Рисунок 1.1 — Выбор масштаба
Если исходить из разрешающей способности 640х480 пикселей (12 режим экрана монитора), то: - количество пикселей по оси Х: 640 – а – а1; - количество пикселей по оси У: b – b1, где а1 и в1 – отступы соответственно с правой и верхней сторон экрана, как показано на рисунке 1.1 Тогда масштабы по осям Х(Мх) и Y(Му) равны:
С учетом Мх и Му координаты точек для оператора PSET будут следующими: В этих формулах учитывается, что по оси абсцисс количество пикселей возрастает при увеличении n, а количество пикселей по оси y убывает. Для проверки правильности выбора а2 и в 2 надо подставить в эти формулы значения nmax и ymax вместо n и y. При этом a2 = 640 – a1, а b2 = b1, то есть, последние значения будут соответствовать значениям отступов. Таким образом, при построении графика следует использовать PSET с координатами (a2,b2):
Таблица переменных программы
В таблице 2.1 приведены глобальные переменные программы и их функциональное значение.
Таблица 2.1— Таблица переменных программы
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.126.43 (0.011 с.) |

 ,
,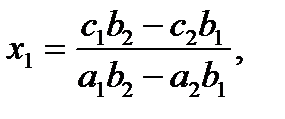

 ,
,  и
и  . При использовании этого метода нелинейное уравнение должно быть приведено к виду
. При использовании этого метода нелинейное уравнение должно быть приведено к виду  - левая часть нелинейного уравнения;
- левая часть нелинейного уравнения;  – первая производная от
– первая производная от  ;
;  .
. производится в этом методе иначе, чем в методе простой итерации, то значения
производится в этом методе иначе, чем в методе простой итерации, то значения  могут использоваться без индексов. Анализ нахождения искомого значения
могут использоваться без индексов. Анализ нахождения искомого значения  .
. .
.
 .
. .
. .
. .
. .
. представить в виде элементов массива;
представить в виде элементов массива;
 .
. .
. .
.


