
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Questions Regarding SkyscrapersСодержание книги
Поиск на нашем сайте The dictionary says (and I trust it’s no lie), a SKYSCRAPER's a VERY TALL BUILDING. Why, how tall, then, is VERY TALL? What rule to apply? Would twenty-six storeys qualify? And besides, skyscrapers should scrape the sky. But I’ve never seen one doing it. Why? Perhaps it’s because the sky’s too high even for skyscrapers. My oh my! But how high, tell me then, is the sky? At what height does it begin? and why? Is it just where the jackdaws cry: or farther up where the aeroplanes fly? or where the satellites orbit by? or where the stars are rich in supply? or where the angels sing lullaby? And, anyway, what on earth is the sky, that it can be scraped? Is it soft as pie (sometimes they say there’s a pie in the sky), or is it hard like a wooden ply, or simply a giant butterfly? I wish I could fly up and try, but the flight, I’m afraid, may go awry. Perhaps I’ll only find out when I die, unless you can tell me, but please don’t lie. If you tell me, I’ll give you a chunk of my pie. Dietrich Hucke Jena, Germany. February 1989
31. Answer the following questions: 1. Why do people wish to build tall structures? 2. How do they manage in high-rise construction? 3. Can you recollect the examples of tall structures from the ancient times and at present? 4. What is the main purpose of building skyscrapers? 5. Can we manage without them? 6. What risks can ultra-high skyscrapers be at?
32. There exist several problems associated with the skyscrapers: 1. Designs should be tested in earthquakes. 2. Skyscrapers should be protected from terrorists’ attacks. 3. Skyscrapers threaten wide views of historic buildings and city skyline. 4. Skyscrapers are big users of electric power. Try to find possible solutions to these problems. What other problems can you mention? Work in pairs.
The following concerns a question in a physics degree exam at the University of Copenhagen: One student replied: "You tie a long piece of string to the neck of the barometer, then lower the barometer from the roof of the skyscraper to the ground. The length of the string plus the length of the barometer will equal the height of the building." This highly original answer so incensed the examiner that the student was failed immediately. The student appealed on the grounds that his answer was indisputably correct, and the university appointed an independent arbiter to decide the case. The arbiter judged that the answer was indeed correct, but did not display any noticeable knowledge of physics. To resolve the problem it was decided to call the student in and allow him six minutes in which to provide a verbal answer that showed at least a minimal familiarity with the basic principles of physics. For five minutes the student sat in silence, forehead creased in thought. The arbiter reminded him that time was running out, to which the student replied that he had several extremely relevant answers, but couldn't make up his mind which to use. On being advised to hurry up the student replied as follows: "Firstly, you could take the barometer up to the roof of the skyscraper, drop it over the edge, and measure the time it takes to reach the ground. The height of the building can then be worked out from the formula H = 0.5g x t squared. But bad luck on the barometer." "Or if the sun is shining you could measure the height of the barometer, then set it on end and measure the length of its shadow. Then you measure the length of the skyscraper's shadow, and thereafter it is a simple matter of proportional arithmetic to work out the height of the skyscraper." "But if you wanted to be highly scientific about it, you could tie a short piece of string to the barometer and swing it like a pendulum, first at ground level and then on the roof of the skyscraper. The height is worked out by the difference in the gravitational restoring force T =2 pi sqr root (l /g)." "Or if the skyscraper has an outside emergency staircase, it would be easier to walk up it and mark off the height of the skyscraper in barometer lengths, then add them up." "If you merely wanted to be boring and orthodox about it, of course, you could use the barometer to measure the air pressure on the roof of the skyscraper and on the ground, and convert the difference in millibars into feet to give the height of the building." "But since we are constantly being exhorted to exercise independence of mind and apply scientific methods, undoubtedly the best way would be to knock on the janitor's door and say to him 'If you would like a nice new barometer, I will give you this one if you tell me the height of this skyscraper'." The student was Niels Bohr, the only Dane to win the Nobel Prize for physics.
Texts for supplementary reading Text 1 Technical Terms Our language is expanding all the time. Whenever new inventions, styles, or ideas are created, old words take on new meanings or new words are added. For example, the word computer took on a new meaning with the invention of the high-speed electronic machine that stores information and performs mathematical and logical calculations. The technical terms software and hardware entered our language.
Use the diagrams to answer these questions: 1. What does the term post mean in architecture? 2. What other meanings does the word have? 3. What does the term keystone refer to? 4. What meaning does capital have in architecture? 5. What other meanings does the word have? 6. What parts make up a column? 7. What parts make up an entablature?
Text 2
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 The Barometer Problem
The Barometer Problem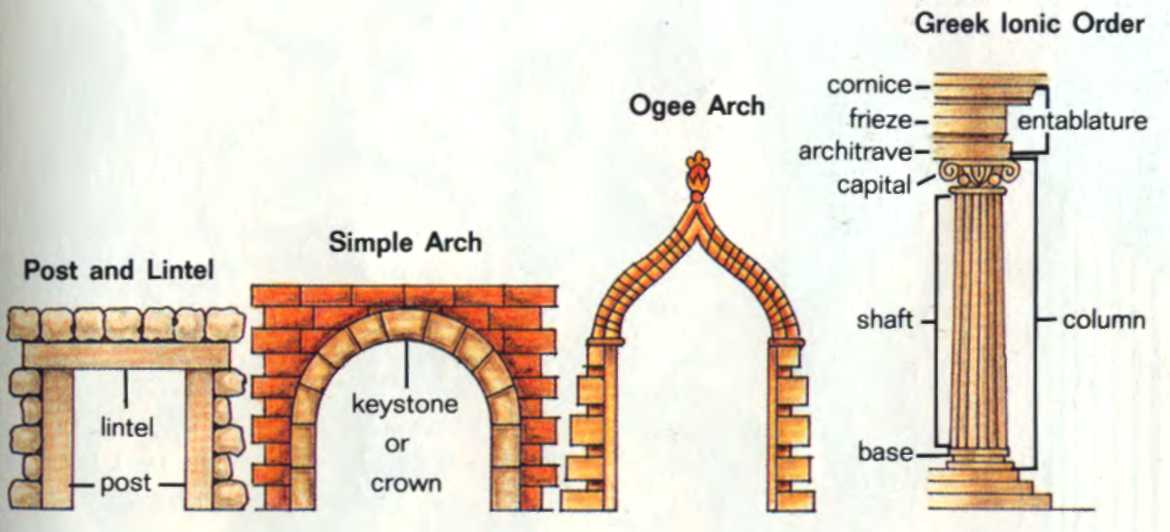 All fields of science and applied arts use technical terms that have particular meanings. The diagrams below will help you understand some technical terms used in architecture.
All fields of science and applied arts use technical terms that have particular meanings. The diagrams below will help you understand some technical terms used in architecture.


