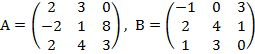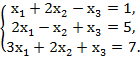Имени Никиты Акинфиевича Демидова»

Имени Никиты Акинфиевича Демидова»

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

по учебной дисциплине

ЕН. 01 Элементы высшей математики

Специальность 080110 «Банковское дело»

для студентов заочного отделения

Филиала

ГАОУ СПО СО «НТГПК им. Н.А. Демидова»

СОДЕРЖАНИЕ

 

	стр.
1. РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
2. Методические указания по выполнению контрольной работы
3. содержание контрольной работы
4. Контрольно-измерительные материалы и комплексные оценочные средства

Паспорт ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

«Элементы высшей математики»

Область применения программы

Программа учебной дисциплины является частью основной образовательной программы в соответствии с ФГОС по специальности СПО 080110 «Банковское дело»

Программа учебной дисциплины может быть использована в дополнительном профессиональном образовании и профессиональной подготовки по другим специальностям:

 

1.2. Место учебной дисциплины в структуре основной профессиональной образовательной программы: дисциплина входит в математический и общий естественнонаучный цикл

1.3. Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:

 

В результате освоения учебной дисциплины обучающийся должен уметь:

 

· решать системы линейных уравнений;

· производить действия над векторами, составлять уравнения прямых и определять их взаимное расположение;

· вычислять пределы функций;

· дифференцировать и интегрировать функции;

· моделировать и решать задачи линейного программирования;

В результате освоения учебной дисциплины обучающийся должен знать:

· основные понятия линейной алгебры и аналитической геометрии;

· основные понятия и методы математического анализа;

· виды задач линейного программирования и алгоритм их моделирования

 

Освоение учебной дисциплины «Элементы высшей математики» способствует формированию общих и профессиональных компетенций:

ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ПК 1.1 Осуществлять расчетно-кассовое обслуживание клиентов.

ПК 1.2. Осуществлять безналичные платежи с использованием различных форм расчетов в национальной и иностранной валютах.

ПК 1.3. Осуществлять расчетное обслуживание счетов бюджетов различных уровней.

ПК 1.4. Осуществлять межбанковские расчеты.

ПК 2.1 Оценивать кредитоспособность клиентов.

ПК 2.3 Осуществлять сопровождение выданных кредитов.

ПК 2.5 Формировать и регулировать резервы на возможные потери по кредитам.

1.4. Рекомендуемое количество часов на освоение программы учебной дисциплины:

максимальной учебной нагрузки обучающегося часов, в том числе:

обязательной аудиторной учебной нагрузки обучающегося часов;

самостоятельной работы обучающегося часов.

СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1. Объем учебной дисциплины и виды учебной работы

Вид учебной работы	Объем часов
Максимальная учебная нагрузка (всего)
Обязательная аудиторная учебная нагрузка (всего)
в том числе:
практические занятия
контрольные работы
Самостоятельная работа обучающегося (всего)
Итоговая аттестация в форме экзамена

2.2. Тематический план и содержание учебной дисциплины Элементы высшей математики

Наименование разделов и тем	Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся, курсовая работа (проект)	Объем часов	Уровень освоения
Раздел 1. Теория пределов.
Тема 1.1. Предел функции. Непрерывность функции	Содержание учебного материала
Предел функции. Замечательные пределы. Виды неопределенностей. Непрерывность функции. Точки разрыва и их классификация.
Практические занятия: вычисления предела функции, раскрытие простейших неопределенностей.
Самостоятельная работа обучающихся: выполнение практических работ по теме «Теория пределов»
Раздел 2. Дифференциальное и интегральное исчисление.
Тема 2.1. Производная функции	Содержание учебного материала
Производная функции одной переменной. Производная сложной функции. Производная обратных функций (обратные тригонометрические функции). Вторая производная и производные высших порядков.
Практические занятия: исследование функции посредством производной и построение графика функции.
Самостоятельная работа обучающихся: выполнение практических работ по теме «Производная функции».
Тема 2.2. Исследование функции с помощью производной	Содержание учебного материала
Схема исследования функции посредством производной и построение графика.
Практические занятия: исследование функции посредством производной и построение графика функции.
Самостоятельная работа обучающихся: Домашняя практическая работа «Исследование функции и построение графика»
Тема 2.3. Неопределенный интеграл	Содержание учебного материала
Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Интегрирование посредством разложения подынтегральной функции на слагаемые, посредством замены переменной, по частям.
Практические занятия: вычисление неопределенного интеграла посредством разложения подынтегральной функции на слагаемые, посредством замены переменной, по частям.
Самостоятельная работа обучающихся: Выполнение практических работ по теме «Неопределенный интеграл»
Тема 2.4. Определенный интеграл	Содержание учебного материала
Определенный интеграл, его свойства. Формула Ньютона-Лейбница. Вычисление определенного интеграла интегрированием по частям и подстановкой.
Практические занятия: вычисление определенного интеграла с помощью формулы Ньютона-Лейбница, интегрированием по частям и подстановкой.
Самостоятельная работа обучающихся: Выполнение практических работ по теме «Определенный интеграл»
Раздел 3. Линейная алгебра с элементами аналитической геометрии.
Тема 3.1. Матрицы, определители	Содержание учебного материала
Матрица, виды матрицы. Действия над матрицами: сложение матриц, умножение матрицы на число, транспонирование матрицы, умножение матриц. Детерминант (определитель) матрицы, его свойства. Обратная матрица.
Практические занятия: действия над матрицами, вычисление определителей.
Самостоятельная работа обучающихся: Выполнение практических работ по теме «Алгебра матриц и определителей».
Тема 3.2. Решение систем линейных уравнений.	Содержание учебного материала
Система линейных алгебраических уравнений (СЛАУ). Методы решения системы линейных алгебраических уравнений: метод Крамера решения невырожденных квадратных линейных систем, метод Гаусса нахождения общего решения.
Практические занятия: решение СЛАУ методом Гаусса и методом Крамера.
Самостоятельная работа обучающихся: Выполнение практических работ по теме «Решение систем линейных уравнений»
Тема 3.3. Аналитическая геометрия на плоскости	Содержание учебного материала
Вектор. Действия над векторами. Уравнения прямой на плоскости. Угол между двумя прямыми. Взаимное расположение двух прямых на плоскости.
Практические занятия: составление уравнения прямых на плоскости. Определение взаимного расположения двух прямых на плоскости.
Самостоятельная работа обучающихся: Выполнение практических работ по теме «Аналитическая геометрия на плоскости»
Раздел 4. Линейное программирование.
Тема 4.1. Общая постановка задачи линейного программирования.	Содержание учебного материала
Понятие и сущность задачи линейного программирования (ЗЛП). Задача использования ресурсов или задача планирования производства. Транспортная задача. Моделирование задачи линейного программирования.
Тема 4.2. Решение задач линейного программирования графическим методом.	Содержание учебного материала
Геометрический метод решения ЗЛП.
Практические занятия: решение ЗЛП геометрическим методом в случае двух переменных.
Самостоятельная работа обучающихся: Выполнение практических работ по темам «Решение простейших ЗЛП геометрическим методом»
Тема 4.3. Решение ЗЛП на ЭВМ с использованием программы Excel	Содержание учебного материала
Надстройка «Поиск решения» программы MS Excel.
Практические занятия: решение ЗЛП с использованием надстройка «Поиск решения» программы MS Excel.
Самостоятельная работа обучающихся: Домашняя практическая проверка «Построение математической модели и решение задачи планирования производства с использованием надстройка «Поиск решения» программы MS Excel»
Всего:

Для характеристики уровня освоения учебного материала используются следующие обозначения:

1. ознакомительный (узнавание ранее изученных объектов, свойств);

2. репродуктивный (выполнение деятельности по образцу, инструкции или под руководством)

3. продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач)

 

3.условия реализации УЧЕБНОЙ дисциплины

 

Требования к минимальному материально-техническому обеспечению

Реализация учебной дисциплины требует наличия учебного кабинета математики;

 

Оборудование учебного кабинета:

-посадочные места по количеству обучающихся;

-рабочее место преподавателя;

-комплект учебно-наглядных пособий по математике;

 

Технические средства обучения:

Компьютер с лицензионным программным обеспечением и мультимедиа проектором.

 

Интернет-ресурсы

1. Математика в помощь школьнику и студенту (тесты по математике online)

http://www.mathtest.ru

2. Портал Allmath.ru — Вся математика в одном месте

http://www.allmath.ru

3. Прикладная математике: справочник математических формул, примеры и задачи с решениями

http://www.pm298.ru

 

 

 

КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

 

Контроль и оценка результатов освоения учебной дисциплины осуществляется преподавателем в процессе проведения занятий и контрольных работ, тестирования, а также выполнения обучающимися индивидуальных заданий.

 

 

Результаты обучения (освоенные умения, усвоенные знания)	Формы и методы контроля и оценки результатов обучения
Умения:
В результате освоения учебной дисциплины обучающийся должен уметь: - решать системы линейных уравнений; - производить действия над векторами, составлять уравнения прямых и определять их взаимное расположение; - вычислять пределы функций; - дифференцировать и интегрировать функции; - моделировать и решать задачи линейного программирования	Устный опрос, тестирование, зачет по темам, контрольная работа, внеаудиторная самостоятельная работа, работа с литературой, выполнение индивидуальных заданий.
Знания:
В результате освоения учебной дисциплины обучающийся должен знать: - основные понятия линейной алгебры и аналитической геометрии; - основные понятия и методы математического анализа; - виды задач линейного программирования и алгоритм их моделирования.	Устный опрос, тестирование, зачет по темам, контрольная работа, внеаудиторная самостоятельная работа, работа с литературой, выполнение индивидуальных заданий.

 

Методические указания

I способ.

Длина отрезка ВС найдена в пункте а). BC = . Осталось найти длину отрезка AD. Для этого найдем координаты точки D.

D(x;y) – точка пересечения прямых AD и ВС.

, .

Найдем длину AD: А (1;1), D (- ),

ед. ²

II способ.

BC =

Расстояние AD можно найти как расстояние от точки A (x₀;y₀) до прямой

BC: Аx+By+C=0 по формуле:

А (1;1), ВС: 5x-y+11=0

 

ед. ²

Вариант 1

1. Найти матрицу C=A+3B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 2

1. Найти матрицу C=2A-B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 3

1. Найти матрицу C=3A+B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 4

1. Найти матрицу C=A-4B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 5

1. Найти матрицу C=4A-B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 6

1. Найти матрицу C=A+2B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 7

1. Найти матрицу C=A-2B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 8

1. Найти матрицу C=A+5B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 9

1. Найти матрицу C=A-5B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 10

1. Найти матрицу C=A-6B, если

2. Решить систему линейных уравнений методом обратной матрицы.

3. Решить систему линейных уравнений по формулам Крамера.

4. Решить систему линейных уравнений методом Гаусса.

 

Вариант 1

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 2

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 3

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 4

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 5

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 6

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 7

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

Вариант 8

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

 

Вариант 9

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

 

Вариант 10

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

1. Вычислить предел функции:

ЛИТЕРАТУРА

Основные источники:

11.Геворкян П. С. Высшая математика. Линейная алгебра и аналитическая геометрия (Гриф Минобразования). / П. С. Геворкян. — М.: ФИЗМАТЛИТ, 2007. — 208 с.

12.Дадаян А.А. Математика для педагогических училищ (рекомендовано ФИРО) — М.: ООО Издательство «Форум», 2006. — 512 с.

13.Дадаян А. А. Сборник задач по математике: учеб. пособие для ссузов. (Гриф Минобразования)— М.: Форум: Инфра-М. 2010. — 352 с.

14.Лакерник А. Р. Высшая математика. Краткий курс: учебное пособие. (Гриф УМО МО РФ) — М.: Логос. 2008. — 528 с.

15.Березина Н.А. Максина Е. П. Математика (рекомендовано ФИРО). — М.: ИД «Риор». 2007. —175 с.

16.Богомолов Н.В., Самойленхо П.И. Математика (рекомендовано ФИРО). — М.: Издательство "Дрофа", 2009. — 397 с.

17.Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для средних специальных учебных заведений (рекомендовано ФИРО). — 2-е изд.— М.: Издательство "Дрофа", 2009. — 236 с.

18.Григорьев С.Г., Задулина СВ. Математика учебник для студ. сред. проф. учреждений (рекомендовано ФИРО). — 3-е изд. — М.: ОИЦ «Академия», 2009. — 384 с.

19.Ланцова О. Ю. Высшая математика для экономистов: курс лекций (Гриф Минобразования России). / О. Ю. Ланцова, Е. Н. Сахарова, В. И. Малыхин. — М.: Экономика, 2010. —351 с.

20.Общий курс высшей математики для экономистов: учебник для вузов. (Высшее образование) (Гриф Мин образования). / общ. ред. В. И. Ермаков. — М.: Инфра-М, 2010. —656 с.

Дополнительные источники:

1. Ахтямов А. М. Математика для социологов и экономистов: учеб. пособие для вузов. — 2-е изд. испр. и доп. —• М.: Физматлит, 2008. — 464 с.

4. Богомолов Н. В. Математика: учебник для ссузов. — 6-е изд.— М.: Дрофа, 2009. — 395 с.

5. Богомолов, Н. В. Сборник задач по математике: учеб. пособие для ссузов. —5-е изд. — М.: Дрофа, 2009. — 204 с.

10.Лунгу К. Н. Линейное программирование: Руководство к решению задач: учеб. пособие для вузов. — 2-е изд. испр. и доп. — М.: Физматлит, 2009. — 132 с.

11.Журбенко Л. Н. Математика в примерах и задачах: учеб. пособие для вузов. / Л. Н. Журбенко, Г. А. Никонова, С. Н. Нуриева. — М.: Инфра-М, 2009. — 372 с.

12.Математика в экономике: учебник для вузов. 4.1. / А. С. Солодовников, В. А. Бабайцев, А. В. Браилов, И. Г.Шандра. — 2-е изд. — М.: Финансы и статистика, 2007. — 384 с.

13. Математика в экономике: учебник для вузов. Ч. 2. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. – 2-е изд. – М.: Финансы и статистика, 2007. – 560 с.

14.Высшая математика: учеб. пособие для вузов. / под ред. С.А. Розанова. – М.: Физматлит, 2009. – 168 с.

15.Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление: учеб. пособие для вузов. – 2-е изд. / под ред. И.М. Петрушко. – СПб.: Лань, 2009. – 288 с.

 

имени Никиты Акинфиевича Демидова»