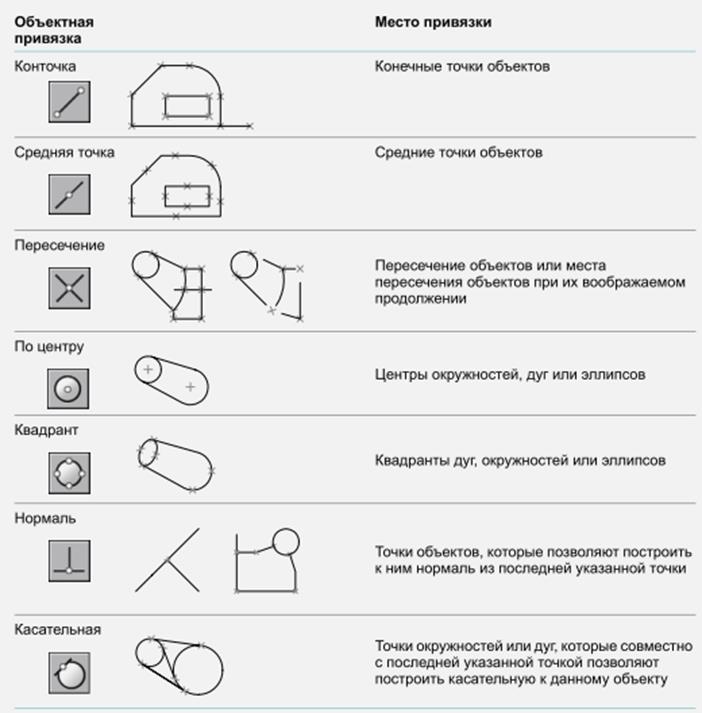
Управление объектной привязкой

 

 

 

Интерполяционные кривые.

Для каждого криволинейного ребра в компьютере хранится либо уравнение кривой, либо эквивалентные характеристические параметры. Эти сведения важны как для систем автоматизированной разработки чертежей, так и для систем объемного моделирования.

Условно все кривые можно подразделять на:

• Апроксимационные

• Интерполяционные

Задачи построения кривых по точкам возникают в компьютерной графике при проектировании, обработке изображений

и распознавании образов. Отыскание кривой, проходящей через заданное множество точек, составляет задачу интерполиро-

вания, а отыскание кривой, проходящей вблизи заданного множества точек, – задачу аппроксимации. Для точной передачи

кривизны по исходным данным удобнее использовать интерполяционные кривые, а если требуется, заодно, и убрать «шум»

в исходных данных, то – аппроксимирующие кривые.

Представьте, что вы работаете в системе геометрического моделирования и хотите визуализировать кривую. Кажется естественным передать системе координаты нескольких точек на этой кривой, а затем соединить их плавной линией при помощи средства, называемого сплайном (spline).

Так же и в САПР: конструктор указывает точки, а система строит по ним интерполяционную кривую, которую и отображает. Уравнение интерполяционной кривой сохраняется для последующей работы с ней. Можно создать кривую, непосредственно указав задающие точки кривой Безье или В-сплайна. Однако большинство конструкторов предпочитают указывать точки, лежащие на самой кривой, и изменять кривую, перемещая ее характеристические точки. Характеристически­ми точками могут быть задающие точки кривой Безье или В-сплайна, если ин­терполяционная кривая относится к одному из этих классов. Возможность строить интерполяционные кривые по точкам очень полезна, если геометрическая модель создается по существующей физической модели.

Интерполяционные сплайны. Как известно, термин "сплайн" происходит от названия чертежного инструмента – тонкой металлической или деревянной линейки, которая изгибается так, чтобы проходить через заданные точки (xi, yi = f(xi)).

Интерполяционные кривые.

Цифровые модели местности

Цифровой моделью местности (ЦММ) называют совокупность точек местности с известными трехмерными координатами и различными кодовыми обозначениями, предназначенную для аппроксимации местности с ее природными характеристиками, условиями и объектами. Кодовые обозначения характеризуют связи между соответствующими точками ЦММ.

Математической моделью местности (МММ) называют математическую интерпретацию цифровых моделей для компьютерного решения конкретных инженерных задач. В зависимости от инженерного назначения математической модели для одной и той же Ц М М может быть использовано несколько различных МММ.

Конечным результатом инженерных изысканий при проектировании на уровне САПР по этой причине является получение крупномасштабных топографических планов и Ц М М на одни и те же участки местности в единой системе координат.

Информационная емкость общей ЦММ при этом существенно больше информационной емкости самых подробных крупномасштабных топографических планов.

Ц М М и М М М используют прежде всего для получения необходимой исходной информации для автоматизированного проектирования (продольные профили земли по оси трассы, поперечные профили, инженерно-геологические разрезы и т.д.).

Возможности цифрового и математического моделирования позволяют в корне изменить технологию проектирования инженерных объектов и требуют изменения технологии и методов сбора, регистрации и представления исходных данных при изысканиях.

Условно цифровые модели местности можно подразделять:

• цифровые модели рельефа

• цифровые модели ситуации

Традиционным способом отображения рельефа на топографических картах является способ горизонталей.

Для большей наглядности иногда применяют цветовую градацию высот

При цифровом моделировании рельефа и геологического строения местности в зависимости от сложности рельефа, ситуационных особенностей местности, способа производства изысканий, задач проектирования, наличия парка современных геодезических приборов, приборов спутниковой навигации, средств геофизической подповерхностной разведки, средств автоматизации и вычислительной техники могут быть сформированы ЦММ с использованием самых разнообразных принципов.

 

Регулярные ЦММ

Цифровой моделью местности (ЦММ) называют совокупность точек местности с известными трехмерными координатами и различными кодовыми обозначениями, предназначенную для аппроксимации местности с ее природными характеристиками, условиями и объектами. Кодовые обозначения характеризуют связи между соответствующими точками ЦММ.

Вопросам разработки различных видов ЦММ было посвящено большое количество исследований. При этом все известные ЦММ можно разбить на три большие группы: регулярные, нерегулярные и статистические.

Регулярные ЦММ

Регулярные ЦММ создают путем размещения точек в узлах геометрических сеток различной формы (треугольных, прямоугольных, шестиугольных), накладываемых на аппроксимируемую поверхность с заданным шагом. Наиболее часто применяют ЦММ с размещением исходных точек в узлах сеток квадратов (рис. а) или равносторонних треугольников (рис. б). Регулярные ЦММ в узлах правильных шестиугольных сеток (рис. в) нашли применение при проектировании нефтепромысловых дорог в условиях равнинного рельефа Западной Сибири.

 

Регулярные модели весьма эффективно использовать при проектировании вертикальной планировки городских улиц, площадей, аэродромов и других инженерных объектов на участках местности с равнинным рельефом. Однако опыт использования ЦММ с регулярным массивом исходных данных показал, что требуемая точность аппроксимации рельефа достигается лишь при очень высокой плотности точек местности, которая в зависимости от категории рельефа должна быть в 5—20 раз выше по сравнению с нерегулярными ЦММ.

Появление высокопроизводительного оборудования с автоматической регистрацией информации по заданному интервалу длины или времени, тем не менее, делает использование регулярных моделей весьма перспективным.