Означення предиката. Область визначення і область істинності.

Предикат – це речення у простому висловленні, які вміщують змінні, і для яких не можна визначити логічну вартість, бо при підстановці замість змінних певних значень вони перетворюються то в істинні, то в хибні висловлення. Предикати можуть бути одномісними, двомісними чи тримісними залежно від кількості змінних. Одномісним предикатом називають речення А(х) із змінною х, яке задане на певній множині Х і при підстановці значень змінної перетворюється в істинне чи хибне судження. Областю визначення предиката А(х) називають множину тих значень змінної х, при яких предикат перетворюється в істинне чи хибне судження. Область істинності предиката А(х) – це множина тих значень змінної, при яких цей предикат перетворюється в істинне судження. Область істинності предиката позначають символічно:

.

 

Дії над предикатами.

Над предикатами виконуються ті ж дії, що й над висловленнями, однак обов’язковою умовою є одна і таж область визначення для предикатів:

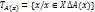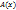1) заперечення предиката А(х), заданого на множині Х – це такий новий предикат , який перетворюється в істинне висловлення при тих значеннях змінної х з області визначення Х, при яких даний предикат А(х) перетворюється в хибне висловлення. Область істинності заперечення предиката, заданого на певній множині – це доповнення до області істинності даного предиката.

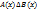2) кон’юнкція двох предикатів А(х) та В(х), заданих на множині Х – це такий новий предикат , який перетворюється в істинне висловлення лише при тих значеннях х з області визначення Х, при яких обидва ці предикати одночасно перетворюються в істинні судження. Область істинності кон’юнкції предикатів – це переріз областей істинності цих предикатів.

3) диз’юнкція двох предикатів А(х) і В(х), заданих на множині Х – це такий новий предикат , який перетворюється в істинне висловлення лише при тих значеннях х з області визначення Х, при яких хоча б один з предикатів перетворюється в істинне висловлення. Область визначення диз’юнкції двох предикатів – це об’єднання областей істинності даних предикатів.

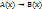4) Імплікація двох предикатів А(х) і В(х), заданих на множині Х – це новий предикат , який перетворюється в хибне висловлення при тих значення х з області визначення Х, при яких предикат А(х) перетворюється в істинне висловлення, а предикат В(х) – в хибне. Область істинності імплікації – це об’єднання доповнень до області істинності предиката А(х) з областю істинності предиката В(х).

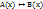5) Еквіваленція двох предикатів А(х) і В(х), заданих на множині Х – це новий предикат , який перетворюється в істинне висловлення при тих значеннях змінної х з області визначення Х, при яких обидва предикати перетворюються у висловлення однакової логічної вартості (або одночасно істинні, або одночасно хибні). Область істинності еквіваленції предикатів – це об’єднання перерізу областей істинності даних предикатів з перерізом доповнень до цих областей істинності.

 

 

Квантори. Операція навішування кванторів. Висловлення з кванторами.

Висловлення можуть утворюватись не лише шляхом надання певного значення змінній предиката, можна утворити висловлення, поставивши перед предикатом одне з слів «будь-який», «довільний», «кожний», «усі»,«існує» та інші. Ці слова називаються кванторами. Розрізняють два види кванторів – квантори загальності і квантори існування. Квантори загальності вживаються за допомогою слів «будь-який», «кожен», «усі», «довільний» та позначається символом . Квантори існування виражаються словами «існує», «хоча б один», «деякі» і позначається символом . Операція навішування кванторів – це операція утворення висловлення з предиката за допомогою кванторів. Логіка часто розглядає предикати, які перетворюються в істинні висловлювання при будь-яких значеннях змінних з області визначення. Такими предикатами є ті, які після операції навішування кванторів виражають властивості арифметичних дій і мають вигляд рівностей. Рівності, які справедливі при будь-яких значеннях змінних, називаються тотожностями.