
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выше поднимется полый цилиндрСодержание книги Поиск на нашем сайте
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ФИЗИКЕ (с решениями) Для специальностей биология, экология, химия дававшихся в 2007-2008 г
СОДЕРЖАНИЕ
1. МЕХАНИКА 2 2. МОЛЕКУЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА 9 3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ 13 4. КОЛЕБАНИЯ И ВОЛНЫ 24 5. ВОЛНОВАЯ И КВАНТОВАЯОПТИКА 27 6. КВАНТОВАЯ ФИЗИКА И ФИЗИКА АТОМА.
МЕХАНИКА
· Закон движения материальной точки: х = 3t + 4t2. Ускорение точки равно … Уравнение равноускоренного движения тела по оси х имеет вид: Или исходя из определений: V = dx/dt, a = dV/dt = d2x/dt2, взяв вторую производную получим: V = 3 + 8t, a = 8. · Закон движения материальной точки по окружности (или вдоль оси х): j = 4t3 +3t (или х = 4t3 + 3t). Угловое ускорение - b (или ускорение - а) через 3 секунды составит … Согласно определениям b = dw/dt (w - угловая скорость), w = dj/dt, откуда, взяв вторую производную получим: w = 12t2 + 3, b = 24t, то есть через 3 секунды это будет 72 рад/с2. Аналогично для линейного движения: a = dV/dt, V = dx/dt или V = 12t2 + 3, a = 24t, то есть через 3 секунды это будет 72 м/с2.
Ускорение при криволинейном движении можно записать Первое слагаемое – тангенциальное ускорение – направлено по касательной к траектории. Поскольку (dV/dt) отрицательно, то оно направлено в сторону 1¢. Второе слагаемое – нормальное (центростремительное) ускорение при движении по окружности всегда направлено к центру окружности, по которой происходит движение (направление 3). Результирующее ускорение 1¢ + 3 будет направлено в сторону 4. Если скорость постоянна, будет направление 3, если скорость растет – 2. Направление 1 (1¢) возможно только при движении по прямой. · Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения … 1) не изменяется 2 ) уменьшается 3) увеличивается Если тангенциальное ускорение отрицательно, то модуль скорости уменьшается. Поскольку аn = V2/R, нормальное ускорение по модулю будет уменьшаться. В случае положительного значения проекции тангенциального ускорения на направления скорости – скорость по модулю будет возрастать и, следовательно, нормальное ускорение тоже будет увеличиваться.
· Точка М движется по спирали с постоянной по величине скоростью. При этом величина нормального ускорения … 1) не изменяется 2) увеличивается 3) уменьшается Поскольку аn = V2/R, нормальное ускорение при постоянном модуле скорости будет уменьшаться при увеличении радиуса (удаление от центра спирали) или увеличивается при движении к центру. · Если а t и а n– тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения: 1) а t = а = const, а n = 0; 2) а t = 0, а n = const; 3) а t = 0, а n = 0; 4) а t = 0, а n ¹ 0 При равномерном движении по окружности модуль скорости не меняется, значит (см. формулу предыдущего теста) а t = 0. Нормальное ускорение отсутствует при равномерном движении по прямой, при равномерном движении по окружности аn = const = V2/R (модуль), но направление меняется. Значит правильно соотношение 4): а t = 0, а n ¹ 0. · Величина скорости автомобиля изменялась во времени, как показано на графике V(t). В момент времени t2 (t1, t3, t4) автомобиль поднимался по участку дуги.
Согласно второму закону Ньютона F = m a, где F – результирующая сила, действующее на тело, а – его ускорение. То есть направление результирующей силы F совпадает по направлению с ускорением а. В момент времени t2 скорость автомобиля не менялась, при этом тангенциальное ускорение аt=0. При движении по дуге на тело действует центростремительное (нормальное) ускорение, направленное к центру окружности, касательной к дуге в этой точке (направление 3) В момент времени t1 скорость возрастала, то есть аt>0, направлено по направлению 5, аn – к центру (направление 3). Суммарное ускорение 3 + 5 направлено по 4. В момент времени t3 скорость уменьшалась, то есть аt<0, направлено по направлению 1. Суммарное ускорение 1 + 3 направлено по 2. Момент времени t4 аналогичен моменту времени t2: аt=0, но V = 0, и, следовательно аn.= 0. · Диск вращается равноускоренно вокруг горизонтальной оси. Укажите направление: 1) вектора угловой скорости точки А на ободе диска. 2) вектора тангенциального ускорения точки А на ободе диска. 3) вектора углового ускорения точки А на ободе диска.
В механике угловой скоростью является вектор (псевдовектор), направленный по оси вращения в сторону, определяемую правилом «буравчика», в данном случае направление 2. Угловая скорость для всех точек вращающегося тела одинакова. Тангенциальное ускорение точки направлено по касательной к траектории, то есть в направлении 3 при ускоренном движении или 1 при замедленном. Угловое ускорение – производная от угловой скорости. Направлено по оси вращения, как и угловая скорость 2 при ускоренном движении или 4 при замедленном.
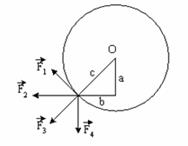
Плечо силы относительно оси вращения проходящей через центр диска это расстояние от оси вращения до прямой, проходящей через вектор силы. Для сил: F 1 – c, F 2 – а, F 3 – 0, F 4 – b. · Тело массой 2 кг поднято над Землей. Его потенциальная энергия 400 Дж. Если на поверхности Земли потенциальная энергия тела равна нулю и силами сопротивления воздуха можно пренебречь, скорость тела после прохождения ¼ расстояния до Земли составит: 10, 14, 20, 40 м/с Закон сохранения энергии ЕК + ЕП = (mV2)/2 + mgh = const = 400 Дж. Для максимальной высоты подъема H запишем: mgH = 400 Дж. Для высоты (3/4)Н (после прохождения ¼ расстояния до Земли): (3mgH)/4 + (mV2)/2 = 400 Дж. Если учесть, что (3mgH)/4 = (400´3)/4 Дж = 300 Дж, то есть в предыдущем уравнении (mV2)/2 = 100 Дж. При весе тела 2 кг, V2 = 200/2 (м/с)2. V = 10 м/с.
1) 2 Дж 2) 15 Дж 3) 10Дж
Работа это скалярное произведение силы на перемещение: А = Fs = Fs cosa = 4 (Н) 5 (м) cos 60° = 10 Дж
· Система состоит из трех тел с массами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг, которые двигаются, как показано на рисунке Если скорости шаров V1 = 3 м/с, V2 = 2 м/с, V3 = 1 м/с, то величина скорости центра масс этой системы равна …м/с 10, 2/3, 5/3, 4.
Скорость центра масс определяется равнением: V Ц = (m1 V 1 + m2 V 2 + m3 V 3)/(m1 + m2 + m3) Следует сразу обратить внимание, что m1 V 1 + m3 V 3 = 0 и центр масс будет двигаться в направлении X со скоростью VЦ = (m2V2)/(m1 + m2 + m3) = 4/6 м/с = 2/3 м/с.
Связь проекции силы FХ с потенциальной энергией запишется: FХ = – (dEП/dх). Если предположить, что EП = ах2, то dEП/dх = ах, учитывая знак «–» выбираем ответ 3. · Тонкостенная трубка и диск имеют одинаковые массы и радиусы Для их моментов инерции справедливо соотношение… 1) Iт < Iд 2) Iт > Iд 3) Iт = Iд Момент инерции тела относительно оси вращения равен I = å miri2, где mi – масса элемента тела, ri – расстояние этого элемента до оси вращения. Очевидно, что любое полое тело будет иметь больший момент инерции, поскольку его масса удалении от оси. Момент инерции трубки будет больше, чем диска. · Диск и цилиндр имеют одинаковые массы и радиусы. Для их моментов инерции справедливо соотношение: 1) Iц < Iд 2) Iц > Iд 3) Iц = Iд
(Другой вариант: кольцо и тонкостенная трубка имеют одинаковые массы и радиусы Для их моментов инерции справедливо соотношение… 1) Iт < Iк 2) Iт > Iк 3) Iт = Iк
С точки зрения динамики вращательного движения относительно оси симметрии тел между телами разницы нет, поэтому Iц = Iд = (mR2)2. (Другой вариант: Iт = Iк = mR2)
· Из жести вырезаны три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на равное расстояние и расставили симметрично оси ОО¢. Для моментов инерции получившихся фигур относительно оси ОО¢ справедливо соотношение …
Момент инерции тела определяется как I = åmiri2, где mi – масса элемента, ri – его расстояние до оси вращения. С этой точки зрения тела 1 и 2 не отличаются друг от друга, то есть I1 = I2. Для третьего тела его элементы находятся ближе к оси вращения, значит его момент инерции меньше, и окончательно I1 = I2 > I3. Правильно соотношение 1). · Сплошной и полый цилиндр имеют одинаковые радиусы и массы. Какой из них выше закатится без проскальзывания по наклонной плоскости, если начальные скорости их одинаковы? 1) Выше поднимется сплошной цилиндр Больше будет скорость шара 3) больше будет скорость полой сферы Задача обратная предыдущей. Начальная потенциальная энергия одинакова и идет на кинетическую энергию поступательного движения и вращения. Поскольку моменты инерции полых тел всегда больше, для их «раскручивания» требуется большая доля энергии, следовательно скорость шара будет больше.
1) 2 2) 1,5 3) 3 4) 4 R = а
Теорема Штейнера связывает момент инерции тела относительно оси, проходящей через центр масс Iц и относительно ½½ ей оси на расстоянии а Iа: Iа = Iц + mа2. Для кольца Iц = mR2 = ma2, Iа = Iц + mа2 = ma2 + ma2 = 2 ma2. Момент инерции увеличится в 2 раза.
Кинетическая энергии тела это энергия его поступательного движения плюс энергия вращательного движения. Для первого тела Ек = m1V2/2 + Iw2/2, где m1 – масса первого тела, V – скорость, I – момент инерции, w - угловая скорость вращения. Для второго тела Ек = m2V2/2. Если скорости и выделившиеся энергии (кинетические энергии, перешедшие в тепло) тел одинаковы, то масса второго тела должна быть больше, так как его энергия состоит только из энергии поступательного движения.
1-й вариант решения. Кинетическая энергия системы не изменилась. Для вращательного движения Ек = Iw2/2. Момент инерции шеста уменьшился, значит, угловая скорость должна увеличиться. 2-й вариант решения. Из основного уравнения вращательного движения твердого тела Ib = N (I – момент инерции тела, b – его угловое ускорение, N – момент внешних сил) следует, что если на тело не действуют внешние силы, то Ib = 0 и, поскольку b = dw/dt (w – угловая скорость),
· График зависимости а мплитуды колебаний груза от частоты приведен на рисунке. Определить максимальную энергию, если жесткость пружины к = 10 Н/м
Энергия максимальна в резонансе, где
1) от нас перпендикулярно плоскости рисунка 2) вверх в плоскости рисунка 3) вниз в плоскости рисунка 4) к нам перпендикулярно плоскости рисунка
Момент силы это векторное произведение [ rF ] = n rFsina, где n – единичный вектор, перпендикулярный плоскости, где лежат вектора rF и направленный по правилу «буравчика», вращающегося от r к F, то есть в положении 1 маятника – к нам перпендикулярно плоскости рисунка. В симметричном относительно вертикали положении направление изменится на противоположное – от нас. Проще можно рассмотреть вращение «буравчика» в направлении качания маятника (указано на рисунках дугой со стрелкой).
· Космический корабль пролетает мимо наблюдателя со скоростью 0,8с. По измерениям наблюдателя его длина равна 90 м. В состоянии покоя его длина наиболее близка к... 1) 90 м 2) 55 м 3) 110 м 4) 150 м При движении со скоростями близкими к скорости света происходит Лоренцовское сокращение отрезков в соответствии с законом
· Космический корабль с двумя космонавтами летит со скоростью 0,8 с ВОЛНОВАЯ И КВАНТОВАЯОПТИКА
· Одна и та же дифракционная решетка освещается различными монохроматическими излучениями с разными интенсивностями. Какой рисунок соответствует случаю освещения светом с наименьшей длиной волны? (J – интенсивность света, j– угол дифракции) Положения максимумов дифракционной решетки определяется формулой: d sinj = 2m (l/2). Если решетка одна и та же, т.е. d = const, то для меньшей длины волны будет меньше и j. Интенсивность на положение максимумов не влияет.
● Радужные пятна на поверхности воды, покрытой тонкой пленкой бензина, объясняются … 1) интерференцией света 2) дифракцией света 3)поляризацией света 4) дисперсией света
Положения максимумов дифракционной решетки определяется формулой: d sinj = 2m (l/2), где m – целое число, определяющее № максимума. Т.о. наименьшей постоянной будет соответствовать большее sinj, т. е. рис. 1). У рис. 2 «неправильная» форма зависимости I(sin j).
· Тонкая пленка вследствие явления интерференции в отраженном свете имеет зеленый цвет. При увеличении показателя преломления пленки ее цвет станет … синим красным не изменится
Разность хода лучей при интерференции в тонких пленках равна: Ds = 2bÖ(n2 – sin2j) – l/2, где b – толщина пленки, n –показатель (коэффициент) преломления, j – угол, под которым ведется наблюдение. Зеленый цвет соответствует условию Ds = mlЗЕЛ (m – целое число). При увеличении показателя преломления Ds увеличится и условие Ds = ml будет выполняться для света с большей длиной волны, т.е. для красного.
· (Вариант). Тонкая пленка вследствие явления интерференции в отраженном свете имеет зеленый цвет. При увеличении толщины пленки ее цвет станет … синим красным не изменится Решение аналогично.
· При падении света из воздуха на диэлектрик отраженный луч полностью поляризован. Преломленный луч распространяется под углом 30 градусов к нормали. При этом падающий луч составляет с нормалью угол 30° 45° 60° 90°
Пользуясь законом преломления можно показать, что луч преломленный при этом перпендикулярен лучу отраженному, т.е. отраженный луч должен распространятся под углом 60° к нормали. Поскольку угол падения равен углу отражения, угол падения тоже 60°.
· (Обратная задача) При падении света из воздуха на диэлектрик отраженный луч полностью поляризован при угле падения 60 градусов. При этом преломленный луч составляет с нормалью угол… Решение аналогично, угол 30°.
· На пути естественного света помещены две пластинки турмалина (два поляризатора). После прохождения первой пластины свет полностью поляризован. Если I1 и I2 – интенсивности света, прошедшего пластины 1 и 2 соответственно, и I2 = (I1/4), то угол между направлениями ОО и О¢О¢ равен: 45, 90 30 или 60 градусов?
q
I1 I2
О О¢
Для поляризованного света, прошедшего через поляризатор (второй) выполняется закон Малюса: I2 = I1 cos2 q. Из условия теста I2 = (I1/4) следует, что cos2 q = ¼, cos q = ½, q = 60°.
· Если увеличить в 2 раза объемную плотность световой энергии, то давление света … увеличится в 4 раза увеличится в 2 раза останется неизменным
где ЕЭ – энергетическая освещённость поверхности, т.е. плотность потока световой энергии электромагнитного излучения падающего перпендикулярно на площадь S плоскости Р; ρ – коэффициент отражения от поверхности; ω – плоскость энергии; Фэ – поток излучения. Связь давления с плотностью световой энергии линейная, т.е. давление увеличится в 2 раза
· Если зачерненную пластинку, на которую падает свет, заменить на зеркальную той же площади, то световое давление … увеличится в 2 раза уменьшится в 2 раза останется неизменным
Для зачерненной пластинки можно считать коэффициент отражения 0, а для зеркала – 1. Согласно формуле предыдущего задания ответ 1).
· На рисунке показана кривая зависимости спектральной плотности энергетической светимости абсолютно черного тела от длины волны при Т=6000К (1). Если температуру тела уменьшить в 4 раза, то длина волны, соответствующая максимуму излучения, …
1) уменьшится в 4 раза 2) уменьшится в 2 раза 3) увеличится в 4 раза
Согласно закону смещения Вина lмакс. = b/Т, то есть если температура уменьшится в 4 раза, во столько же раз должна увеличиться длина волны максимума, т.е. ответ 3).
· (Вариант) На рисунке показаны кривые зависимости спектральной плотности энергетической светимости абсолютно черного тела от длины волны при разных температурах. Если длина волны, соответствующая максимуму излучения, увеличилась в 4 раза, то температура абсолютно черного тела уменьшилась в 2 раза уменьшилась в 4 раза увеличилась в 2 раза увеличилась в 4 раза
Закону смещения Вина lмакс. = b/Т. Если длина волны максимума увеличилась в 4 раза, то температура в 4 раза уменьшилась.
· (Вариант). На рисунке показаны кривые зависимости спектральной плотности энергетической светимости абсолютно черного тела от длины волны при разных температурах. Если кривая 2 соответствует спектру излучения абсолютно черного тела при температуре 1500 К, то кривая 1 соответствует температуре (в К) … 1000 6000 3000 750 Пользоваться законом смещения Вина.
· На рисунке показаны направления падающего фотона (g), рассеянного фотона (g¢) и электрона отдачи (е). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол j = 30°. Если импульс падающего фотона Р¡ (Вариант: Если импульс электрона отдачи Pе … то импульс рассеянного фотона равен Р ¡¢ …)
1) Ö3 2) 2Ö3 3) 1,5 4) 1,3Ö3
При эффекте Комптона выполняются законы сохранения энергии и импульса.
· Для некоторого материала фотокатода на рисунке приведена прямая а, соответствующая зависимости энергии фотоэлектронов от частоты падающего света. При замене материала фотокатода на материал с меньшей работой выхода зависимость будет соответствовать прямой…. b c d a.
Для фотоэффекта Эйнштейн установил h v = (mV2)/2 + A, где h – постоянная планка, v – частота падающего света, (mV2)/2 – кинетическая энергия выбиваемого фотоэлектрона, A – работа выхода материала. Точка пересечения прямой с осью v соответствует красной границе фотоэффекта, когда энергия кванта света (фотона) равна работе выхода материала. Если А2 < А1 то энергия (mV2)/2 = h v – A будет больше и кривая пойдет параллельно первой и выше, т.е. будет b.
· На рисунках приведены вольтамперные характеристики вакуумного фотоэлемента при разных освещенностях (а) и разных частотах падающего на него света (б). Для данных случаев справедливы соотношения…
При увеличении частоты увеличится энергия квантов света и соответственно электронов, поэтому увеличится запирающее напряжение – кривая 2, рис. б). Если интенсивности света одинаковы, токи насыщения тоже будут равны.
· На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электрона с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Наименьшей (наибольшей) частоте кванта в серии Пашена (Лаймана, Бальмера) соответствует переход…
Согласно постулату Бора излучение происходит при переходе электрона с одной стационарной обиты на другую. Частота и энергия связаны соотношением Е = h v = hс/l т.е. большей частоте в любой серии соответствует большая энергия перехода или соответственно меньшая длина волны.
· Де-Бройль обобщил соотношение p = h/l на любые микрочастицы, импульс которых равен р. Если длины волн де-Бройля частиц одинаковы, то наибольшей скоростью обладает … 1) a-частица 2) нейтрон 3) протон 4)электрон Если длины волн равны, равны и импульсы частиц. р = mV, следовательно скорость будет наибольшей у самой легкой частицы, т.е. у электрона.
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ФИЗИКЕ (с решениями) Для специальностей биология, экология, химия дававшихся в 2007-2008 г
СОДЕРЖАНИЕ
1. МЕХАНИКА 2 2. МОЛЕКУЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА 9 3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ 13 4. КОЛЕБАНИЯ И ВОЛНЫ 24 5. ВОЛНОВАЯ И КВАНТОВАЯОПТИКА 27 6. КВАНТОВАЯ ФИЗИКА И ФИЗИКА АТОМА.
МЕХАНИКА
· Закон движения материальной точки: х = 3t + 4t2. Ускорение точки равно … Уравнение равноускоренного движения тела по оси х имеет вид: Или исходя из определений: V = dx/dt, a = dV/dt = d2x/dt2, взяв вторую производную получим: V = 3 + 8t, a = 8. · Закон движения материальной точки по окружности (или вдоль оси х): j = 4t3 +3t (или х = 4t3 + 3t). Угловое ускорение - b (или ускорение - а) через 3 секунды составит … Согласно определениям b = dw/dt (w - угловая скорость), w = dj/dt, откуда, взяв вторую производную получим: w = 12t2 + 3, b = 24t, то есть через 3 секунды это будет 72 рад/с2. Аналогично для линейного движения: a = dV/dt, V = dx/dt или V = 12t2 + 3, a = 24t, то есть через 3 секунды это будет 72 м/с2.
Ускорение при криволинейном движении можно записать Первое слагаемое – тангенциальное ускорение – направлено по касательной к траектории. Поскольку (dV/dt) отрицательно, то оно направлено в сторону 1¢. Второе слагаемое – нормальное (центростремительное) ускорение при движении по окружности всегда направлено к центру окружности, по которой происходит движение (направление 3). Результирующее ускорение 1¢ + 3 будет направлено в сторону 4. Если скорость постоянна, будет направление 3, если скорость растет – 2. Направление 1 (1¢) возможно только при движении по прямой. · Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения … 1) не изменяется 2 ) уменьшается 3) увеличивается Если тангенциальное ускорение отрицательно, то модуль скорости уменьшается. Поскольку аn = V2/R, нормальное ускорение по модулю будет уменьшаться. В случае положительного значения проекции тангенциального ускорения на направления скорости – скорость по модулю будет возрастать и, следовательно, нормальное ускорение тоже будет увеличиваться.
· Точка М движется по спирали с постоянной по величине скоростью. При этом величина нормального ускорения … 1) не изменяется 2) увеличивается 3) уменьшается Поскольку аn = V2/R, нормальное ускорение при постоянном модуле скорости будет уменьшаться при увеличении радиуса (удаление от центра спирали) или увеличивается при движении к центру. · Если а t и а n– тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения: 1) а t = а = const, а n = 0; 2) а t = 0, а n = const; 3) а t = 0, а n = 0; 4) а t = 0, а n ¹ 0 При равномерном движении по окружности модуль скорости не меняется, значит (см. формулу предыдущего теста) а t = 0. Нормальное ускорение отсутствует при равномерном движении по прямой, при равномерном движении по окружности аn = const = V2/R (модуль), но направление меняется. Значит правильно соотношение 4): а t = 0, а n ¹ 0. · Величина скорости автомобиля изменялась во времени, как показано на графике V(t). В момент времени t2 (t1, t3, t4) автомобиль поднимался по участку дуги.
Согласно второму закону Ньютона F = m a, где F – результирующая сила, действующее на тело, а – его ускорение. То есть направление результирующей силы F совпадает по направлению с ускорением а. В момент времени t2 скорость автомобиля не менялась, при этом тангенциальное ускорение аt=0. При движении по дуге на тело действует центростремительное (нормальное) ускорение, направленное к центру окружности, касательной к дуге в этой точке (направление 3) В момент времени t1 скорость возрастала, то есть аt>0, направлено по направлению 5, аn – к центру (направление 3). Суммарное ускорение 3 + 5 направлено по 4. В момент времени t3 скорость уменьшалась, то есть аt<0, направлено по направлению 1. Суммарное ускорение 1 + 3 направлено по 2. Момент времени t4 аналогичен моменту времени t2: аt=0, но V = 0, и, следовательно аn.= 0. · Диск вращается равноускоренно вокруг горизонтальной оси. Укажите направление: 1) вектора угловой скорости точки А на ободе диска. 2) вектора тангенциального ускорения точки А на ободе диска. 3) вектора углового ускорения точки А на ободе диска.
В механике угловой скоростью является вектор (псевдовектор), направленный по оси вращения в сторону, определяемую правилом «буравчика», в данном случае направление 2. Угловая скорость для всех точек вращающегося тела одинакова. Тангенциальное ускорение точки направлено по касательной к траектории, то есть в направлении 3 при ускоренном движении или 1 при замедленном. Угловое ускорение – производная от угловой скорости. Направлено по оси вращения, как и угловая скорость 2 при ускоренном движении или 4 при замедленном.
|

 · Материальная точка М движется по окружности со скоростью V. На первом рисунке показан график зависимости проекции скорости Vt (t - единичный вектор положительного направления, Vt - проекция V на это направление). При этом вектор полного ускорения на втором рисунке имеет направление …
· Материальная точка М движется по окружности со скоростью V. На первом рисунке показан график зависимости проекции скорости Vt (t - единичный вектор положительного направления, Vt - проекция V на это направление). При этом вектор полного ускорения на втором рисунке имеет направление …


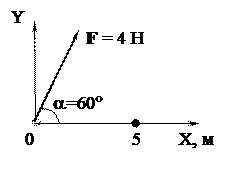 · На рисунке показан вектор силы, действующей на частицу. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5;0), равна …
· На рисунке показан вектор силы, действующей на частицу. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5;0), равна …
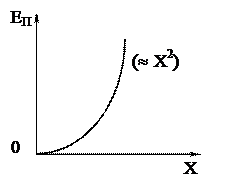 · В потенциальном поле сила F пропорциональна – градиенту потенциальной энергии ЕП. Если график зависимости потенциальной энергии ЕП от координаты Х имеет вид, то зависимость проекции силы FХ на ось Х будет …
· В потенциальном поле сила F пропорциональна – градиенту потенциальной энергии ЕП. Если график зависимости потенциальной энергии ЕП от координаты Х имеет вид, то зависимость проекции силы FХ на ось Х будет …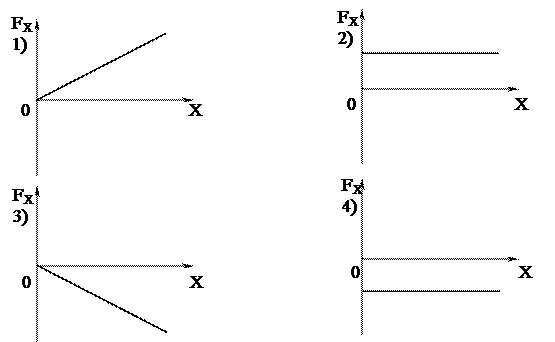



 · При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкого кольца перенести из центра масс на край (рис.), то момент инерции относительно новой оси увеличится в … раза.
· При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкого кольца перенести из центра масс на край (рис.), то момент инерции относительно новой оси увеличится в … раза. Энергия пружины определяется уравнением Е = (кА2)/2.
Энергия пружины определяется уравнением Е = (кА2)/2.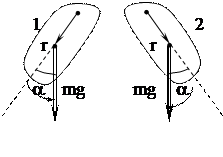 · Физический маятник совершает колебания вокруг оси, проходящей через точку О перпендикулярно плоскости рисунка. Куда направлен момент силы тяжести:
· Физический маятник совершает колебания вокруг оси, проходящей через точку О перпендикулярно плоскости рисунка. Куда направлен момент силы тяжести: , т.е. для длины покоящегося корабля l 0 получим: 90/Ö1–(v2/c2) = 90/0,6 = 150м.
, т.е. для длины покоящегося корабля l 0 получим: 90/Ö1–(v2/c2) = 90/0,6 = 150м.
 · Имеются 4 дифракционных решетки с различными постоянными d (периодами решетки), освещаемые одним и тем же монохроматическим излучением различной интенсивности. Какой рисунок иллюстрирует положение главных максимумов, создаваемых дифракционной решеткой с наименьшей постоянной решетки?
· Имеются 4 дифракционных решетки с различными постоянными d (периодами решетки), освещаемые одним и тем же монохроматическим излучением различной интенсивности. Какой рисунок иллюстрирует положение главных максимумов, создаваемых дифракционной решеткой с наименьшей постоянной решетки?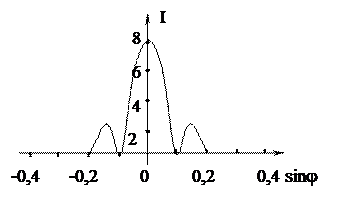
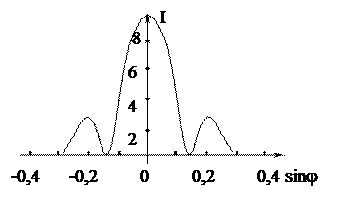
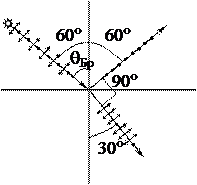 Полная поляризация при отражении происходит при падении света на границу раздела под углом Брюстера, который определяется соотношением tgqБр = n2/n1, где n2 и n1, – коэффициенты преломления сред.
Полная поляризация при отражении происходит при падении света на границу раздела под углом Брюстера, который определяется соотношением tgqБр = n2/n1, где n2 и n1, – коэффициенты преломления сред. О О¢
О О¢ ,
,
 4) увеличится в 2 раза
4) увеличится в 2 раза
 Согласно второму (см. нижний рис.)
Согласно второму (см. нижний рис.) 

 На рисунке а) приведены две вольтамперные характеристики вакуум-ного фотоэлемента, соответствующие разным освещенностям, при этом для графика 1 освещенность больше, чем для графика 2. Для большей освещенности график идет выше, фототок насыщения больше. В то же время запирающее напряжение UЗ при котором ток прекращается одинаково, так как оно определяется энергией выбиваемых электронов (см. предыдущее задание).
На рисунке а) приведены две вольтамперные характеристики вакуум-ного фотоэлемента, соответствующие разным освещенностям, при этом для графика 1 освещенность больше, чем для графика 2. Для большей освещенности график идет выше, фототок насыщения больше. В то же время запирающее напряжение UЗ при котором ток прекращается одинаково, так как оно определяется энергией выбиваемых электронов (см. предыдущее задание).


