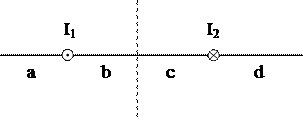Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение максимума зависит от природы газа (массы молекул).Содержание книги
Поиск на нашем сайте
· В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота. Распределение скоростей молекул гелия будет описывать кривая (приведены три кривые аналогичные предыдущей). Согласно предыдущему примеру с ростом массы молекул максимум будет смещаться влево, поскольку масса стоит в знаменателе. · Средняя кинетическая энергия молекул газа при температуре Т зависит от их структры, что связано с возможностью различных видов движения атомов в молекуле. Средняя кинетическая энергия молекул гелия (Не) равна …
1) (5/2)kT 2) (1/2)kT 3) (3/2)kT 4) (7/2)kT
Средняя кинетическая энергия молекул газа при температуре Т равна Числом степеней свободы тела i называют число независимых координат, полностью определяющих положение тела в пространстве. а) молекулы, состоящие из одного атома, можно представить материальной точкой, положение которой полностью определяется заданием трех ее координат. Одноатомные молекулы (He, Ar) имеет i = 3, ответ 3).
в) молекулы из трех и более жестко связанных атомов, не лежащих на одной прямой, полностью определяются тремя координатами центра инерции (x, y, z) и тремя углами вращения (θ, γ, ψ) вокруг осей (OX, OY, OZ). N – атомная молекула (N ≥ 3) имеет i = 6: три степени поступательные и три – вращательные. г) если многоатомная молекула N ≥ 2 имеет упругую связь, то в системе может возникнуть колебательное движение. Нужно учесть и его колебательные (от 1 и более). Колебательная степень свободы должна иметь энергию, вдвое большую по сравнению с поступательной или вращательной. Это объясняется тем, что колебательное движение связано с наличием кинетической и потенциальной энергий. На колебательные степени свободы приходится энергия в два раза больше: Еколеб = kT. Колебательные степени свободы возбуждаются при высоких температурах, что должно специально оговариваться.
· Средняя кинетическая энергия молекул газа при температуре Т равна 1) 3 2) 5 3) 7 8)
· При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно
1) 3 2) 5 3) 6 4) 8 · Состояние идеального газа определяется значением параметров T0, p0 и V0. Определенное количество газа перевели из состояния (3p0, V0) в состояние (p0, 2V0) при этом его внутренняя энергия … 1) не изменилась 2) увеличилась 3) уменьшилась Уравнение состояния идеального газа pV = v RT. Первому состоянию соответствует изотерма Т1 = (3p0V0)/ v R, второму – Т2 = (2p0V0)/ v R. Внутренняя энергия идеального газа пропорциональна температуре. Поскольку Т1 > Т2, внутренняя энергия газа уменьшилась.
· Если DU – изменение внутренней энергии идеального газа, А – работа газа, Q – теплота, сообщаемая газу, то для изобарного нагревания газа справедливы соотношения … 1) Q > 0; А > 0; DU = 0 2) Q > 0; А = 0; DU > 0 3) Q > 0; А > 0; DU > 0 4) Q = 0; А < 0; DU > 0 Согласно первому началу термодинамики Q = U + А – тепло переданное системе идет на увеличение ее внутренней энергии и совершение работы. При изобарном нагреве Q > 0, давление постоянно, т.е. работа
· В процессе обратимого адиабатического нагревания постоянной массы идеального газа его энтропия … 1) уменьшается 2) не изменяется 3) увеличивается Для обратимого процесса dS = dQ/T. При адиабатическом процессе обмена теплом не происходит: dQ = 0, значит, энтропия не меняется.
· На рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Теплота подводится к системе на участке…
Цикл Карно состоит из двух изотерм: 1-2, 3-4 и двух аддиабат: 2-3, 4-1. При адиабатическом процессе система по определению не обменивается теплом с внешней средой. При изотермическом процессе энтропия (степень «беспорядка») будет расти с ростом температуры, то есть на участке 1-2.
На той же диаграмме адиабатное расширение происходит на участке … 1) 1-2 2) 2-3 3) 3-4 4) 4-1 При адиабатическом расширении температура падает, значит. расширению будет соответствовать участок 2-3.
Отношение работ, совершенных в каждом цикле А1/А2 будет равно …
1) 2 2) -1/2 3) -2 4) 1/2
На диаграмме р-V работа А = рdV равна площади под кривой и будет отрицательна, если объем уменьшается. Работа в первом цикле А1 = 3 «клетки», во втором цикле А = 6 «клеток» и в обоих случаях положительна. А1/А2 = ½. Работа отрицательной в любом из циклов при изменении направлении обхода контура.
· На (р,V) диаграмме изображен циклический поцесс. На каких участках температура
 1) растет 1) растет
2) уменьшается 3) остается постоянной
При изобарных процессах (АБ и СД) PV = RT, Р = RT/V т.е. Т растет, где растет V и наоборот. На изохорных участках ДА и БС PV = RT, V = RT/ Р т.е. температура растет с возрастанием давления и наоборот.
3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
· Электростатическое поле создано одинаковыми по величине точечными зарядами q1 и q2. Куда направлен вектор напряженности поля в точке С, если q1 = –q, q2 = +q, расстояния а равны.
Для напряженности поля имеем: Е = (1/4pe0) Q/r2 e r. Направлен вектор напряженности электрического поля вдоль прямой, проходящей через данную точку и заряд (от заряда, если заряд положительный, к заряду, если заряд отрицательный). Поскольку расстояние от положительного заряда до точки С в два раза меньше, поле созданное им будет больше и направление будет от заряда – 3.
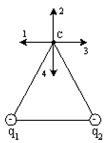
· q1 = q2 = –q; q1, q2, С – образуют равнобедренный треугольник. Указать направление поля Е.
Поле заряда q1 направлено по стороне Сq1 в сторону заряда, а заряда q2 по стороне Сq2 в сторону заряда q2. Суммарное поле направлено по 4.
· Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы, то поток вектора напряженности электростатического поля Е через поверхность сферы: увеличится, уменьшится или не изменится? Согласно теореме Гаусса, поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0:
· Точечный заряд +q находится в центре сферической поверхности. Если заряд сместить из центра сферы, оставляя его внутри нее, то поток вектора напряженности электростатического поля через поверхность сферы.. В соответствии теоремой Гаусса (предыдущее задание) поток определяется суммарным зарядим внутри сферы, т.е он не изменится.
· Поле создано точечным зарядом +q. Укажите направление вектора градиента потенциала в точке А. · Поле создано равномерно заряженной сферической поверхностью с зарядом –q. Укажите направление вектора градиента потенциала в точке А. · Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда +s. Укажите направление вектора градиента потенциала в точке А
В первых двух случаях Еr = –dj/dr, в третьем Еу = –dj/dу. Градиент потенциала (и любой другой величины) показывает направление его наибольшего увеличения. Таким образом, он будет направлен противоположно вектору Е: В первом случае к заряду. Во втором случае от центра сферы. В третьем случае в направлении плоскости.
· Обкладки плоского конденсатора имеют поверхностные плотности заряда +s и –2s соответственно как выглядит Е и j вне и между пластин?
Направим ось х как показано на рисунке, совместив 0 с +s пластиной. В области 1 поле от +s пластины Е = s/e0, направлено – х. Поле от В области 2 направления полей совпадают с направлением х, и результирующее поле будет Е = 3s/e0. В области 3 поле пластины +s направлено по х, поле пластины –2s направлено – х. Результирующее поле Е = 2s/e0,наравлено – х. Ех = –dj/dх, тогда j будет, как изображено на рисунке. Начало координат не принципиально, поскольку j определяется с точностью до const. Вариант задания: заряды +2s и –s. Картинки для Е и j симметрично перевернуться относительно оси х.
· Если система зарядов в пространстве создает электрическое поле в областях 1-2-3 как показано на рисунке, то потенциал будет иметь вид (связь между Е и j: Ех = –dj/dх):
· В электрическом поле плоского конденсатора перемещается заряд +q в направлении, указанном стрелкой. Работа сил поля на участке АВ:
положительна, отрицательна или равна нулю. Работа сил поля по определению работы А = Fdl = Fdlcosj – скалярное произведение силы на перемещение (j – угол между F и dl). Электрическое поле и сила, действующая на положительный заряд направлены от + к –. В первом случае перемещение ^ силе, j = 90° и работа равна нулю. Во втором случае направление перемещения совпадает с направлением силы, j = 0 и работа положительна.
· На рисунке показана зависимость силы тока в электрической цепи от времени. Заряд, прошедший по проводнику на интервале времени от 10 до 20 с (в мКл) равен … 20 c Согласно определению тока I = dQ/dt или dQ = Idt или Q = òIdt, 10 c а это есть площадь под указанной кривой на заданном интервале времени.
· Жесткий электрический диполь находится в однородном электростатическом поле. Момент сил, действующих на диполь, направлен… к нам вдоль вектора напряженности поля от нас против вектора напряженности поля
Момент пары сил, действующих на диполь будет стремится повернуть его в направлении, указанном на рисунке. «Буравчик», вращающийся в этом направлении будет двигаться к нам, т.е. также к нам направлен момент сил.
· Рамка с током с магнитным дипольным моментом, направление которого указано на рисунке, находится в однородном магнитном поле. Рамка с током аналогична диполю. Магнитный момент диполя направлен от отрицательного заряда к положительному, как указано на рисунке. Задача сводится к предыдущей.
· При помещении неполярного диэлектрика в электростатическое поле 1) происходит ориентирование имевшихся электрических дипольных моментов молекул; вектор поляризованности образца направлен по направлению внешнего поля 2) в образце присутствуют только индуцированные упругие электрические дипольные моменты атомов; вектор поляризованности образца направлен против направления внешнего поля 3) в образце присутствуют только индуцированные упругие электрические дипольные моменты атомов; вектор поляризованности образца направлен по направлению внешнего поля 4) происходит ориентирование имевшихся электрических дипольных моментов молекул; вектор поляризованности образца направлен против направления внешнего поля У неполярного диэлектрика центр отрицательных зарядов смещается против поля, положительных зарядов – по полю, т.е. дипольный момент индуцируется. Направление дипольного момента от центра отрицательных зарядов к центру положительных, т.е. по полю 3). У полярных диэлектриков очевидно ответ 1).
· На рисунке представлены графики, отражающие характер зависимости поляризованности Р диэлектрика от напряженности поля Е.
Укажите зависимость, соответствующую неполярному диэлектрику. Для неполярного диэлектрика Р = c Е, то есть изменяется линейно с полем.
Энергия конденсатора W=СU2/2, где С – емкость конденсатора, U – величина приложенного напряжения. Емкость плоского конденсатора С = ee0S/d, где
· На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2 от напряженности электрического поля Е.
Определить отношение удельных проводимостей этих элементов. Закон Ома в дифференциальной форме имеет вид: j = s E. Поэтому отношение s1/s2 будет равно 2.
1-й вариант решения. Сопротивление проводника R = rl/S, где r – удельное сопротивление материала, l и S – длина и сечение проводника. У второго проводника сечение меньше, значит, его сопротивление будет больше. При последовательном включении ток в проводниках одинаковый, а напряжение (U = IR) будет больше там, где больше сопротивление, то есть на втором проводнике. Напряженность электрического поля Е = U/l (Е = –dU/dl), тоже будет больше во втором проводнике. 2-й вариант решения. Закон Ома в дифференциальной форме имеет вид: j = sE, где j – плотность тока, s – удельная проводимость материала, E – напряженность электрического поля. Ток протекающий по проводникам одинаковый, значит во втором проводнике плотность тока больше, а следовательно больше и напряженность электрического поля.
· Зависимость удельного сопротивления металлического проводника от температуры соответствует графику · Зависимость удельного сопротивления проводника от температуры в области сверхроводящего перехода представлена графиком
· Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если 2I1 = I2, то вектор магнитной индукции В результирующего поля в точке А направлен: вниз, вверх, влево, вправо
Проводник с током I2 в два раза ближе к точке А и ток в нем в два раза больше, значит он и будет определять направление поля – вверх. · На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем
На интервалах b и c магнитные поля создаваемые проводниками направлены в одну сторону, поэтому нуля быть не может. На интервалах a и d В направлено в противоположные стороны. Но поскольку I1 = 2I2, на участке а В от проводника I1 превосходит поле от проводника I2 и нулю равно быть не может. На участке d найдется точка, где суммарное магнитное поле будет равно нулю. Учитывая, что величина магнитного поля проводника с током определяется уравнением B = 2I/l (l – расстояние до проводника) и I1 = 2I2, для этой точки будет выполняться условие:
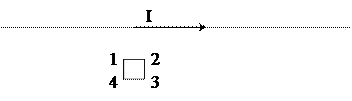
· На рисунке показан длинный проводник с током, около которого находится небольшая проводящая рамка.
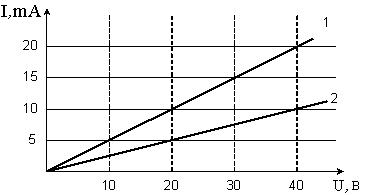
При выключении тока в проводнике указанного направления, в рамке возникнет индукционный ток направления 1-2-3-4, 4-3-2-1 или тока не возникнет? Согласно закону электромагнитной индукции Фарадея ЭДС = – dФ/dt, где знак минус (правило Ленца) указывает, что направление индукционного тока (знак ЭДС) таково, что бы препятствовать причине его вызывающей. Направление В (поток Ф через контур) направлен от нас, значит если ток выключить, в контуре индукционный ток должен поддерживать уменьшающийся поток, то есть направлен по 1-2-3-4. · Вольт-амперная характеристика активных элементов цепи 1 и 2 представлена на рисунке.
На элементе 1 при напряжении 30 В выделится мощность: (На.элементе 2 при напряжении 20 В выделится мощность:) 15 Вт, 0,45 Вт, 0,30 Вт, 450 Вт, 0,1 Вт, 100 Вт? Мощность тока определяется уравнением: P = IU. На элементе 1 при напряжении 30 В: Р = 30 В ´ 15 мА = 450 мВт = 0,45 Вт. На элементе 2 при напряжении 20 В: Р = 20 В ´ 5 мА = 100 мВт = 0,1 Вт.
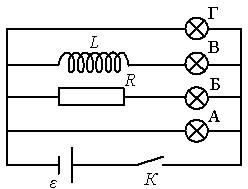
· Индуктивность контура зависит от: - скорости изменения магнитного потока сквозь поверхность, ограниченную контуром - материала, из которого изготовлен контур - силы тока, протекающего в контуре - формы и размеров контура, магнитной проницаемости среды Индуктивность катушки L ~ mm0n2Sl, где m - магнитная проницаемость сердечника (среды), m0 – магнитная постоянная, n – число витков катушки, S – площадь контура, l – размер катушки. · После замыкания ключа К в цепи, представленной на рисунке, загорится позже других лампочка: А, Б, В, Г? Или они загорятся все одновременно?
При замыкании ключа ток в цепи с индуктивностью за счет явления самоиндукции ток будет нарастать постепенно, поэтому лампочка В загорится в полный накал позже.
· На каком интервале времени ЭДС индукции контура максимальна?
ЭДСИНД = –dФ/dt = –d(ВS)/dt, где Ф – магнитный поток пронизывающий контур, В – значение магнитной индукции, S – площадь витков контура. ЭДС максимальна там, где максимальна скорость изменения В, то есть на участке 7.
Варианты предыдущей задачи: · На рисунке представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. - ЭДС индукции в контуре отрицательна и по величине максимальна (минимальна) на интервале - ЭДС индукции в контуре положительна и по величине максимальна (минимальна) на интервале - ЭДС индукции в контуре не возникает на интервале Поскольку ЭДСИНД = –dФ/dt = –d(ВS)/dt, а площадь контура не меняется, графики для В и Ф ведут себя аналогичным образом. ЭДС не возникает на участках 2, 4, 6, 8. Отрицательна (положительна) там, где поток растет (падает), что следует из знака (–) в законе. Максимальна (минимальна) там, где скорость изменения, т.е. угол наклона прямой, максимален (минимален).
· На рисунке представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую парамагнетикам. Укажите зависимость, соответствующую ферромагнетикам. Укажите зависимость, соответствующую диамагнетикам.
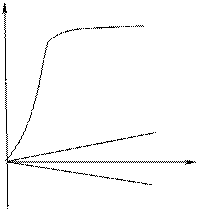 Зависимость намагниченности вещест-ва I от магнитного поля Н дается соот-ношением I =æ Н (æ – магнитная восприимчивость). Зависимость намагниченности вещест-ва I от магнитного поля Н дается соот-ношением I =æ Н (æ – магнитная восприимчивость).
По способности намагничиваться все вещества делятся на 3 группы: парамагнетики (æ > 0), диамагнетики (æ < 0), и ферро-магнетики(æ > 0). Парамагнетики и диамаг-нетики – слабомагнитны, ферромагнетики – сильно. Графики I(Н) для них имеют вид:
· При помещении парамагнетика в стационарное магнитное поле… 1) происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен против направления внешнего поля 2) у атомов индуцируются магнитные моменты; вектор намагниченности образца направлен против направления внешнего поля 3) у атомов индуцируются магнитные моменты; вектор намагниченности образца направлен по направлению внешнего поля 4) происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен по направлению внешнего поля
У парамагнетиков имеется некомпенсированный магнитный момент атомов, направлен случайным образом, поэтому в магнитном поле происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен по направлению внешнего поля 4). У диамагнетиков атомные магнитные моменты скомпенсированы и в магнитном поле у атомов индуцируются магнитные моменты, причем вектор намагниченности образца направлен против направления внешнего поля 2). У ферромагнетиков имеются области (домены) где некомпенсированные магнитные моменты соседних атомов направлены в одном направлении. В магнитном поле области (домены) «благоприятно» ориентированные сначала быстро растут (крутой участок графика предыдущего задания), потом направление намагниченности поворачивается в направлении внешнего поля.
Сила Ампера, действующая на проводник с током в магнитном поле определяется формулой Fl = S dl [ j B ] = I [ dl B ], направление ее определяется по правилу «буравчика» при его вращении от j (I) к B. Чтобы буравчик «ввинчивался», вращение должно быть по часовой стрелке, значит, магнитная индукция направлена «вниз». Можно воспользоваться правилом «левой руки»: силовые линии входят в ладонь, пальцы – по направлению тока, большой палец – направление силы.
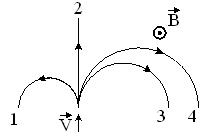
· На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы 3 q = 0, q > 0, q < 0.
Сила Лоренца, действующая на заряженную частицу, движущуюся в магнитном поле со скоростью v равна F = q [ v B ] = n q v B sina. Направление векторного произведения определяется по правилу буравчика и направлено вправо, значит заряд частицы q > 0.
· Ионизированные изотопы магния 24Mn и 25Mn с одинаковой энергией Ек влетают в магнитное поле, направленное перпендикулярно скоростям. Как относятся радиусы их траекторий? Для сил, действующих на ионизированные атомы, имеем F = q [ V B ]. Под действием этой силы частицы летят по окружностям, радиусы которых находятся из соотношения: mV2/R = q V B, R = (mV)/qB, откуда · Полная система уравнений Максвелла для электромагнитного поля имеет вид: Следующая система уравнений
ò(E d l) = – ò(¶ B /¶t)d S ò(E d l) = – ò(¶ B /¶t)d S (L) (S) (L) (S)
ò(H d l) = ò(j + ¶ D /¶t)d S ò(H d l) = ò(¶ D /¶t)d S (L) (S) (L) (S)
ò(D d S) = òrdV ò(D d S) = 0 (S) (V) (S)
ò(B d S) = 0 ò(B d S) = 0 (S) (S)
Справедлива для электромагнитного поля… 1) в отсутствие заряженных тел и токов проводимости 2) в отсутствии заряженных тел 3) при наличии заряженных тел и токов проводимости 4) в отсутствии токов проводимости
В данном тесте требуется внимательно сравнить и проанализировать уравнения первой и второй системы:
Левые части систем одинаковы В правой части уравнения 2 данной системы отсутствует слагаемое j (плотность токов проводимости), значит токи проводимости отсутствуют. Правая часть уравнения 3 данной системы равна нулю, то есть отсутствует r – плотность электрических зарядов. Таким образом, правильный ответ 1).
4. КОЛЕБАНИЯ И ВОЛНЫ
· Для сферической волны справедливо утверждение … 1) амплитуда волны не зависит от расстояния до источника колебаний (при условии, что поглощением среды можно пренебречь)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.01 с.) |

 б) Положение двухатомной молекулы полностью определяется заданием трех координат центра инерции (x,y,z) и двух углов θ и ψ вращения вокруг осей OX и OZ. Вращением вокруг оси ОУ можно пренебречь, т.к. момент инерции её относительно оси ОУ пренебрежительно мал. Двухатомная молекула имеет i = 5: три степени свободы поступательные и две – вращательные.
б) Положение двухатомной молекулы полностью определяется заданием трех координат центра инерции (x,y,z) и двух углов θ и ψ вращения вокруг осей OX и OZ. Вращением вокруг оси ОУ можно пренебречь, т.к. момент инерции её относительно оси ОУ пренебрежительно мал. Двухатомная молекула имеет i = 5: три степени свободы поступательные и две – вращательные.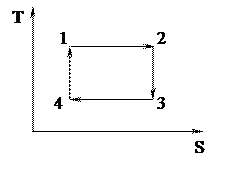 1) 1-2 2) 2-3 3) 3-4 4) 4-1
1) 1-2 2) 2-3 3) 3-4 4) 4-1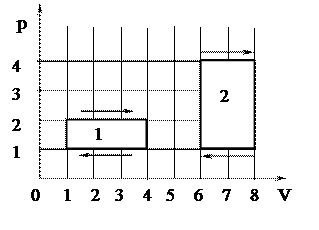 · На (р,V) диаграмме изображены два циклических поцесса.
· На (р,V) диаграмме изображены два циклических поцесса.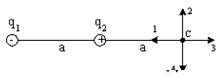

 ФЕ = Q/e0. Таким образом поток то поток вектора напряженности электростатического поля Е через поверхность сферы определяется только зарядами внутри поверхности. Линии поля внешних зарядов будут пересекать поверхность дважды: «входить» и «выходить» и потока не создадут. QВН
ФЕ = Q/e0. Таким образом поток то поток вектора напряженности электростатического поля Е через поверхность сферы определяется только зарядами внутри поверхности. Линии поля внешних зарядов будут пересекать поверхность дважды: «входить» и «выходить» и потока не создадут. QВН

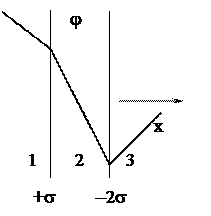

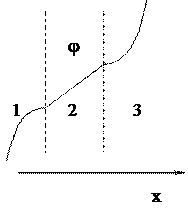


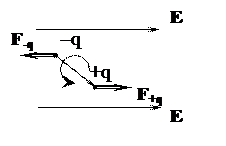
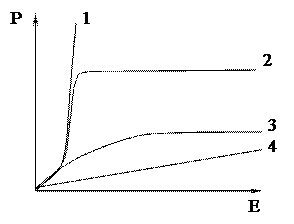
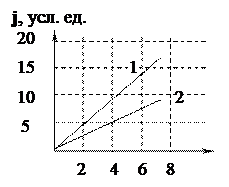
 В области сверхпроводящего перехода удельное сопротивление скачком падает до нуля для всех материалов. Для металлов сростом температуры удельное сопротивление линейно возрастает. Для полупроводников экспоненциально уменьшается.
В области сверхпроводящего перехода удельное сопротивление скачком падает до нуля для всех материалов. Для металлов сростом температуры удельное сопротивление линейно возрастает. Для полупроводников экспоненциально уменьшается. Магнитная индукция В в точке на расстоянии b от проводника с током I определяется уравнением B = m0 2I /4pb, направление определяется по правилу буравчика, то есть направления поля этих проводников противоположно: I1 – вниз, а I2 – вверх.
Магнитная индукция В в точке на расстоянии b от проводника с током I определяется уравнением B = m0 2I /4pb, направление определяется по правилу буравчика, то есть направления поля этих проводников противоположно: I1 – вниз, а I2 – вверх.