
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Швидкість розвитку високоеластиченої деформації.Содержание книги
Поиск на нашем сайте
Припустимо, що до зразка полімеру прикладена постійна напруга, яка значно менша від напруги руйнування. Якщо процеси течії при цьому не відбуваються, то під впливом прикладеної напруги зразок поступово подовжуватиметься до досягнення певної довжини, що не змінюється більше в часі. Поступовий розвиток деформації пов’язаний з тим, що під впливом сил, що діють на полімер, процес зміни конформацій ланцюгів набуває певної спрямованості і вимагає часу. Відносна деформація, яка не змінюється в часі, називається рівноважною високоеластичною деформацією і позначається Кожному значенню напруги відповідає певне значення рівноважної деформації. Ці величини зв’язані співвідношенням, аналогічним закону Гука:
де Доки значення Деформація, що розвинулася за даний проміжок часу, пов’язана з напругою рівнянням
де Оскільки Після зняття напруги, коли зразок відновлює свою первинну форму, також відбувається зміна деформації в часі. Аналогічні явища спостерігаються і при деформації стиснення. Якщо процеси течії відсутні, тобто має місце суто високоеластична деформація, розміри зразка відновлюються повністю, але для цього може знадобитися дуже тривалий проміжок часу. Таким чином, високоеластична деформація залежить не тільки від величини прикладеної напруги, але і від часу дії сили. Релаксація напруги
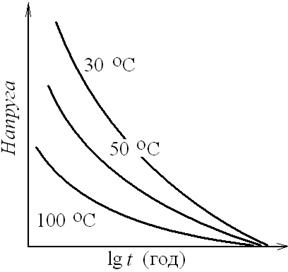
Якщо піддати полімерний зразок дуже швидкій (теоретично миттєвій) деформації і закріпити його в деформованому стані, то за такий короткий проміжок часу рівноважна деформація не може розвинутися. У зразку при цьому виникає напруга, рівна На рис. 2. представлені типові криві релаксації напруги аморфних полімерів. З рисунка видно, що зменшення напруги в зразку відбувається тим швидше, чим вища температура. Вимірюючи напругу в зразку із заданою величиною розтягування, можна розрахувати модуль, який називається модулем релаксації (або релаксаційним модулем) Вивчаючи процес релаксації напруги можна визначити деякі структурні особливості полімерних систем. Найбільш інформативними характеристиками структури сітчастих полімерів є: Ø Число відрізків (ланок) молекулярних ланцюгів, які знаходяться між двома сусідніми вузлами тривимірної сітки, що припадає на одиницю об’єму – NС (величина, що характеризує ступінь поперечного зшивання гуми); Ø Середня маса відрізка (ланки) молекулярного ланцюга (МС), який знаходиться між двома сусідніми вузлами тривимірної сітки в г/моль або у вуглецевих одиницях. Величини NС і МС входять до наступних формул Уолла, які добре описують деформацію еластомерів в області малих і середніх деформацій:
де s ¥ – умовна внутрішня напруга одновісної деформації, розрахована на початковий переріз зразка, Н/м2; NС –число ланок молекулярного ланцюга, які знаходяться між двома сусідніми вузлами тривимірної сітки, що припадає на 1 м3; k – постійна Больцмана, 1,38×10-23Дж/К; Т – температура, К; l ¥ – відносна рівноважна довжина зразка під навантаженням; r – густина З формул Уолла (1) можна виразити шукані характеристики структури еластичного сітчастого полімеру:
Методика виконання роботи 1. З пластини вулканізованої гуми завтовшки ~1-2 мм вирізати 3 зразки у вигляді смужки шириною 1 см і довжиною 20-25 см. 2. На кінцях смужок зробити петлі для закріплення на гачку динамометра та утримувача штатива і пронумерувати зразки. 3. У середині зразків розмітити робочу ділянку довжиною l 0 = 25мм. Виміряти товщину і ширину робочої ділянки зразків штангенциркулем та лінійкою не менше трьох разів і записати середнє значення до таблиці. 4. Один кінець першого зразка гуми закріпити у верхній частині штатива на гачку (або в затискачі) динамометра, а нижній кінець швидко розтягнути вниз і зачепити за нижній утримувач штатива так, щоб покази динамометра були не менше 4000 г. 5. Включити секундомір і фіксувати покази динамометра. Вони відображають початкове значення зовнішнього зусилля Р0, прикладеного до зразка, і відповідно значення протидіючої сили, що виникає в зразку. 6. Потім записують поточні покази динамометра Рt: Ø протягом першої хвилини – через кожні 15 с; Ø протягом подальших 5 хвилин – через кожну хвилину; Ø протягом останніх хвилин – через кожні 2 хвилини. 7. Вимірювання закінчити, коли перестануть змінюватися покази динамометра. 8. У кінці вимірювання, не знімаючи зразка з приладу, заміряти і записати досягнуту в розтягнутому стані рівноважну довжину робочої ділянки між мітками зразка l ¥ . 9. Аналогічно дослідити решту зразків гуми. 10. Всі початкові і отримані дані занести до таблиці. 11. За отриманими даними побудувати графік залежності зусилля (та відповідно внутрішньої протидіючої сили) від часу витримки Р = f (t) (криву релаксації напруги ). 12. З графіка знайти час релаксації t при даній температурі досліду (час встановлення рівноваги після прикладення навантаження до зразка). 13. Екстраполюючи лінійну частину кривої, коли зусилля досягає постійної величини (Р = соnst), на вісь зусилля Р, знайти рівноважне зусилля Р ¥ (в Ньютонах) і потім розрахувати рівноважну напругу в зразку s ¥ за формулою:
де S = b × h – площа поперечного перерізу зразка, мм2; К – поправка до показів приладу, рівна 0,95. 14. Використовуючи формули (2) та (3) визначити структурні характеристики досліджуваних полімерних гум.
Контрольні запитання 1. Охарактеризуйте фізичні стани у аморфних полімерах. 2. Яка природа високоеластичної деформації. 3. Термодинаміка високоеластичної деформації. 4. Чим відрізняються в’язко-пружні і пружно-в’язкі полімери. Навести приклади. 5. Охарактеризуйте основні фізичні моделі в’язкопрожної деформації. 6. Що таке релаксація полімерних макромолекул? 7. Дайте визначення часу релаксації, якими законами він описується? 8. У чому полягає фізична суть процесу релаксації напруги?
ЛАБОРАТОРНА РОБОТА № 7
ВИВЧЕННЯ ОСНОВНИХ ЕЛЕКТРИЧНИХ ХАРАКТЕРИСТИК ПОЛІМЕРІВ
Мета роботи: а) ознайомлення з одним із методів визначення електричних характеристик полімерів; б) визначення об’ємної та поверхневої електропровідності полімерних систем. Прилади та матеріали: тераомметр Е6-13А; з’єднувальні дроти; вимірювальна комірка з круглими електродами різних діаметрів; полімерні зразки; мікрометр; пінцет.
Короткі теоретичні відомості
За електричними властивостями полімери можна розділити на діелектрики, напівпровідники і електропровідні матеріали. До діелектриків відносяться більшість як полярних, так і неполярних полімерів. Полярні діелектрики містять електричні диполі, здатні до переорієнтації у зовнішньому електричному полі. До напівпровідників відносяться полімери з системою з’єднаних зв’язків і полімерні комплекси з переносом заряду. Електропровідними матеріалами є, здебільшого, полімерні діелектрики з введеними в них дрібнодисперсними електропровідними наповнювачами (наприклад, технічним вуглецем, графітом, порошкоподібними металами). Поведінка полімерів в електричному полі визначається такими характеристиками, як діелектрична проникність і діелектричні втрати, електропровідність (або питомий об’ємний і питомий поверхневий електричний опори), електрична міцність. Електричні властивості визначають також прояв у полярних полімерів електретного ефекту і термодеполяризації. Електричні властивості полімерів залежать від хімічної будови і фізичного стану полімерів, від умов їх досліджень і експлуатації, зокрема від амплітуди напруженості зовнішнього поля, температури, вологості середовища, конструкції електродів і геометричних розмірів досліджуваного зразка. Вивчення електричних властивостей полімерів проводять не тільки для оцінки їх експлуатаційних якостей, але й для дослідження хімічної будови і структури полімерів.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.007 с.) |

 . Рівноважна деформація завжди більша будь-якої деформації, що розвинулася за даний проміжок часу t (
. Рівноважна деформація завжди більша будь-якої деформації, що розвинулася за даний проміжок часу t ( ).
). ,
, – рівноважний модуль еластичності.
– рівноважний модуль еластичності. ,
,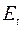 – модуль, який характеризує деформацію, що розвинулася за даний проміжок часу t.
– модуль, який характеризує деформацію, що розвинулася за даний проміжок часу t. .
.
 . Оскільки модуль
. Оскільки модуль  . Час вимірювання може бути стандартизовано, наприклад, встановлено рівним 10 с. Тоді вимірювана величина релаксаційного модуля позначатиметься як
. Час вимірювання може бути стандартизовано, наприклад, встановлено рівним 10 с. Тоді вимірювана величина релаксаційного модуля позначатиметься як  .
. та
та  , (1)
, (1) (2)
(2) (3)
(3) ,
,


