
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Міцність похилих перетинів на поперечну силуСодержание книги
Поиск на нашем сайте
Беручи до уваги, що для підкранової балки основною являється навантаження в вигляді рухомих зосереджених сил, розрахунок на міцність похилих перетинів на поперечну силу виконуємо вирахувавши попередньо всі величин для важкого бетону: Визначаємо коефіцієнт
де при Визначаємо коефіцієнт
де:
Тоді при
Оскільки,
Знаходимо необхідну інтенсивність хомутів, приймаючи довжину проекції похилого перетину Поперечна сила на відстані
Оскільки
Оскільки Виконуємо перевірку похилої смуги між похилими тріщинами.
де
де Оскільки Міцність похилих перетинів на дію згинального моменту
Міцність похилих перетинів при грані опори, а також по довжині зони анкетування напружених елементів, армованих стержнями без анкерування, необхідно перевіряти по згинальному моменту. При цьому опір арматури знижується множенням на коефіцієнт умов роботи арматури Довжина зони передачі напруження арматури для напруженої арматури без анкерів визначаємо по формулі п. 2.29 [3]:
де Рисунок 1.9. До розрахунку на міцність похилого перетину підкранової балки по згинальному моменту
Значення Початок зони анкерування при поступовій передачі зусилля обтиску приймаємо при торці балки. Розрахунковим буде перетин, що починається на грані опори, тобто на відстані Коефіцієнт умов роботи арматури, табл. 23 [8]: для попередньо напруженої арматури:
Розрахунковий опір арматури в місці її перетину похилим перетином (рис.3.9):
Приймаючи в запас міцності те, що в межах похилого перетину навантаження в вигляді зосереджених сил відсутнє, визначаємо довжину проекції найбільш невигідного по згинальному моменту похилого перетину:
де:
Розрахунковий згинальний момент від зовнішнього навантаження в кінці похилого перетину, тобто на відстані
Значення коефіцієнтів При Так як нейтральна вісь при розрахунку нормального перетину на міцність проходить в межах полички, приблизно приймаємо
Тоді граничний згинальний момент, що сприймається похилим перетином, при
Тобто міцність похилого перетину по згинальному моменту забезпечена. Розрахунок прогинів балки Прогин підкранової балки від деформації згину визначаємо при Кривизну залізобетонних елементів без тріщин на ділянці в розтягнутій зоні визначаємо згідно п. 4.24,[3]. Кривизна від короткочасної дії кранового навантаження:
де:
Кривизна від тривалої дії довготривалого навантаження:
де: Кривизна від нетривалої дії попереднього обтиску бетону:
Кривизна, що обумовлена вигином елемента внаслідок усадки і повзучості бетону від зусилля попереднього обтиску бетону:
де:
Відносні деформації бетону на рівні крайнього стиснутого волокна приймаємо приблизно рівними деформаціям бетону на рівні центра тяжіння арматури
Оскільки
Повний прогин балки при відсутності тріщин в розтягненій зоні визначається по формулі:
де:
Тоді
При відношенні
де:
де:
Відносний прогин балки:
Тобто прогини не перевищують допустимого значення.
|
||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.21.89 (0.009 с.) |

 ,
,  ,
,  (п. 3.31, 3.32, [3]).
(п. 3.31, 3.32, [3]). , що враховує вплив стиснутих поличок в таврових і двотаврових перетинах:
, що враховує вплив стиснутих поличок в таврових і двотаврових перетинах: ,
,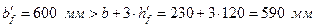 ;
; в розрахунок вводиться величина
в розрахунок вводиться величина  .
. , що враховує вплив попереднього напруження поздовжньої арматури. Для цього визначимо зусилля попереднього обтиску з врахуванням всіх втрат
, що враховує вплив попереднього напруження поздовжньої арматури. Для цього визначимо зусилля попереднього обтиску з врахуванням всіх втрат  при коефіцієнті точності попереднього напруження арматури
при коефіцієнті точності попереднього напруження арматури  :
: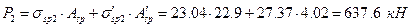
 ;
; ;
; .
. :
: .
. , тому приймаємо
, тому приймаємо 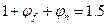

 рівною довжині від опори до першого вантажу
рівною довжині від опори до першого вантажу 
 (з огинаючих епюр).
(з огинаючих епюр).

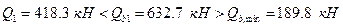 , перевіримо умову:
, перевіримо умову: ;
;
 , поперечну арматуру приймаємо з конструктивних міркувань. Приймаємо
, поперечну арматуру приймаємо з конструктивних міркувань. Приймаємо  А400С (
А400С ( ) з кроком 250 мм.
) з кроком 250 мм.

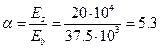 ;
;  ;
; 


 для тяжкого бетону,
для тяжкого бетону, 
 , міцність бетону стінки на ділянці між похилими тріщинами достатня.
, міцність бетону стінки на ділянці між похилими тріщинами достатня. .
. .
. і
і  при армуванні елементів стержневою арматурою згідно табл. 28 [3]:
при армуванні елементів стержневою арматурою згідно табл. 28 [3]:
 при розрахунку на міцність приймаємо рівним більшому з двох значень
при розрахунку на міцність приймаємо рівним більшому з двох значень  і
і  . Так як
. Так як 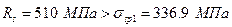 в формулу вводимо величину
в формулу вводимо величину  , де
, де 
 від торця балки (рис.3.9).
від торця балки (рис.3.9). .
. .
. ,
, ;
; з огинаючих епюр;
з огинаючих епюр; - розрахунковий опір для поперечної арматури класу А400С;
- розрахунковий опір для поперечної арматури класу А400С; - площа перетину одного стержня поперечної арматури;
- площа перетину одного стержня поперечної арматури; - кількість стержнів;
- кількість стержнів; - крок поперечних стержнів;
- крок поперечних стержнів;

 - рівномірно розподілене навантаження.
- рівномірно розподілене навантаження. від осі опори:
від осі опори: .
. визначаємо по інтерполяції при
визначаємо по інтерполяції при  , а
, а  в залежності від
в залежності від  .
.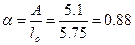 і
і  , коефіцієнт
, коефіцієнт  (табл.10 дод.5 [2]).
(табл.10 дод.5 [2]). .
.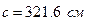 :
:
 .
. і
і  (нормативне навантаження).
(нормативне навантаження). ,
, ;
; ;
; для важкого бетону.
для важкого бетону. ,
,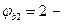 враховуючи вплив тривалої повзучості бетону.
враховуючи вплив тривалої повзучості бетону. ,
, ,
, і
і  відносні деформації бетону, викликані його усадкою і повзучістю від зусилля попереднього обтиску, визначаються відповідно на рівні центра тяжіння розтягненої поздовжньої арматури і крайнього стиснутого волокна бетону по формулах:
відносні деформації бетону, викликані його усадкою і повзучістю від зусилля попереднього обтиску, визначаються відповідно на рівні центра тяжіння розтягненої поздовжньої арматури і крайнього стиснутого волокна бетону по формулах: ;
; 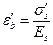
 ,
, .
. . Тоді при
. Тоді при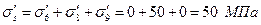 ,
, .
.
 приймаємо
приймаємо  .
. ,
, повна кривизна елемента,
повна кривизна елемента, коефіцієнт, що визначається в залежності від схеми завантаження статично визначеної балки. При рівномірно розподіленому навантаженні
коефіцієнт, що визначається в залежності від схеми завантаження статично визначеної балки. При рівномірно розподіленому навантаженні  , при розрахунку підкранової балки на дію вертикального кранового навантаження приймаємо
, при розрахунку підкранової балки на дію вертикального кранового навантаження приймаємо 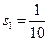 .
.
 .
. необхідно враховувати вплив поперечних сил на прогин балки. Для коротких елементів
необхідно враховувати вплив поперечних сил на прогин балки. Для коротких елементів  повний прогин визначається за формулою:
повний прогин визначається за формулою: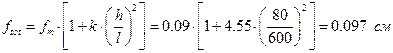 ,
, прогин, обумовлений деформацією згину;
прогин, обумовлений деформацією згину; при відсутності нормальних і похилих тріщин,
при відсутності нормальних і похилих тріщин, ,
, ;
; ;
;




