
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление угла на две равные частиСодержание книги
Поиск на нашем сайте
Для того чтобы разделить угол АВС пополам нужно провести биссектрису из вершины угла. Построение биссектрисы выполняется в следующей последовательности: · · Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К; Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части (рис. 55). Деление прямого угла на три равные части Деление прямого угла АВС на три равные части выполняется в следующей последовательности: ·
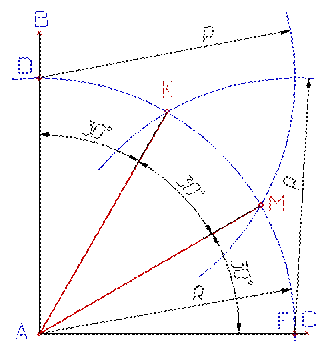
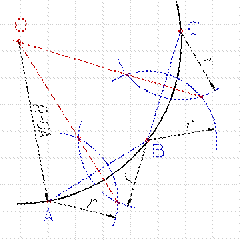
· Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения с дугой DF в точках К и М; · Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части (рис. 56).
Определение центра дуги окружности Нахождение положения центра и величины радиуса данной дуги окружности выполняется в следующей последовательности: 1. На дуге произвольно выбирают три точки A, В и С; 2. Соединяют выбранные точки отрезками (хордами); К отрезкам АВ и ВС через их середины восстанавливают перпендикуляры;
Построение касательных Построение касательной к окружности Касательную из точки А к окружности можно провести следующим образом: 1. На отрезке ОА как на диаметре строят окружность радиуса R=0,5[OA]; 2. Точки 1 и 2 пересечения полученной окружности с заданной определяют положение точек касания;
Построение внешней касательной к двум дугам окружности Внешнее касание к двум дугам разного диаметра выполняется следующим образом:
2. К полученной окружности строят касательную МO*, проходящую через центр дуги меньшего радиуса; 3. На продолжении луча ОМ отмечаем точку касания 1; 4. Из центра O* проводим луч параллельный ОМ до пересечения с дугой и отмечаем точку касания 2; 5. Через точки 1 и 2 проводим искомую касательную t (рис. 59). Построение внутренней касательной к двум дугам окружности
1. Проводят окружность радиусом R+r из центра О дуги большего радиуса; 2. К полученной окружности строят касательную МO*, проходящую через центр дуги меньшего радиуса;
5. Через точки 1 и 2 проводим искомую касательную t (рис. 60).
Скругление углов Скругление прямого угла Cкругление прямого угла, имеющего вершину О, дугой радиуса R осуществляется в следующей последовательности: 1. Из вершины О проводят дугу заданным радиусом R, до пересечения со сторонами угла в точках А и В (точки сопряжения);
3. Проводят дугу АВ радиусом R и центром О1 (рис. 61).
Скругление острого угла Скругление острого угла дугой радиуса R можно выполнить в следующей последовательности: 1. Геометрическим местом точек, равноудаленных от сторон угла, будут являться прямые, параллельные сторонам угла и проходящие от них на расстоянии R; 2. Точка пересечение этих прямых определяет центр скругления О1;
4. Поводим дугу АВ из центра О1 радиусом R (рис. 62). Скругление тупого угла Скругление тупого угла производится точно так же, как и острого. Можно несколько изменить ход построения, если воспользоваться биссектрисой угла: 1. Строят биссектрису угла; 2. Проводят прямую, параллельную одной из сторон угла и отстоящую от нее на расстоянии R;
4. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В; 5. Поводим дугу АВ из центра О1 радиусом R (рис. 63).
Сопряжение
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.10.207 (0.005 с.) |

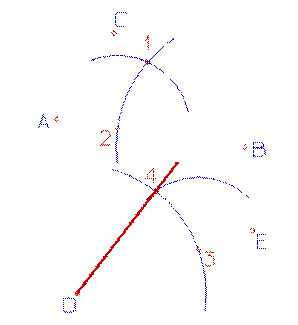 Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;
Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F; Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;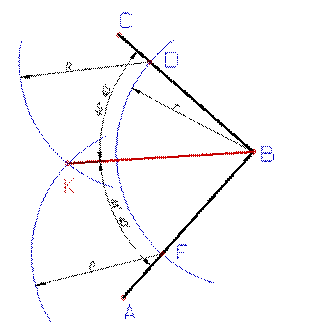
 3. Точка О пересечения перпендикуляров определяет положение центра дуги, а отрезок ОА равен радиусу дуги (рис. 57).
3. Точка О пересечения перпендикуляров определяет положение центра дуги, а отрезок ОА равен радиусу дуги (рис. 57).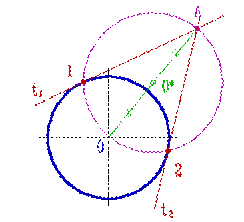
 3. Отрезки [1A] и [2A] определяют положение касательных t1 и t2 проведенных из точки А к окружности (рис. 58).
3. Отрезки [1A] и [2A] определяют положение касательных t1 и t2 проведенных из точки А к окружности (рис. 58).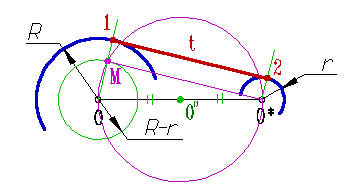
 1. Проводят окружность радиусом R-r из центра О дуги большего радиуса;
1. Проводят окружность радиусом R-r из центра О дуги большего радиуса;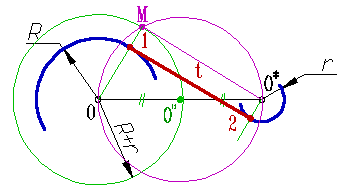 Внутреннее касание к двум дугам разного диаметра выполняется следующим образом:
Внутреннее касание к двум дугам разного диаметра выполняется следующим образом: 3. На луче ОМ отмечаем точку касания 1 - точка пересечения луча с дугой радиуса R;
3. На луче ОМ отмечаем точку касания 1 - точка пересечения луча с дугой радиуса R;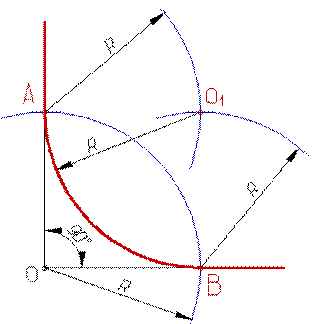 4. Из центра O* проводим луч параллельный ОМ до пересечения с дугой радиуса r и отмечаем точку касания 2;
4. Из центра O* проводим луч параллельный ОМ до пересечения с дугой радиуса r и отмечаем точку касания 2;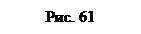 2. Центр скругления О1 должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла АОВ и определяется точкой пересечения дуг радиуса R, проведенных из точек сопряжения А и В;
2. Центр скругления О1 должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла АОВ и определяется точкой пересечения дуг радиуса R, проведенных из точек сопряжения А и В;
 3. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В;
3. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В;
 3. Точка пересечения этой прямой с биссектрисой определяет положение центра скругления О1;
3. Точка пересечения этой прямой с биссектрисой определяет положение центра скругления О1;


