
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визуализация трехмерных моделейСодержание книги Поиск на нашем сайте
Как отмечалось выше, для каждой точки модели объекта фиксируется интенсивность отраженного сигнала, которая может быть использована для визуализации объекта в так называемых псевдоцветах. Для получения реальных плотностей в каждой точке сканирования в сканере применяется цифровая камера, основанная на матрице ПЗС (рис.2). С помощью этой камеры сначала получают серию изображений, покрывающих весь объект в пределах предполагаемого сканирования. Затем объект сканируется, а соответствующие плотности берутся с этих снимков. Такой подход позволяет в последующей обработке оперировать не только с облаком точек лазерного сканирования, но и с цифровыми изображениями объекта, что существенно повышает информативность полученной информации об объекте. Рассмотрим более подробно получение плотностей изображения для каждой точки сканирования со снимков. Итак, сначала производится съемка всего объекта путем поворотов и наклонов камеры (или соответствующего зеркала) с помощью моторов последовательно на углы равные углам поля зрения камеры (рис.2). Здесь стрелками показаны возможные повороты и наклоны камеры в системе координат сканера.
Рис.2
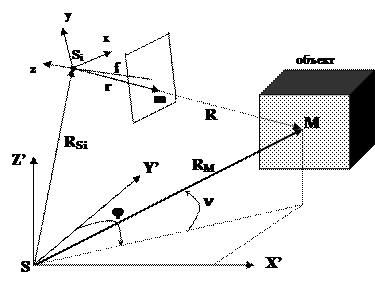
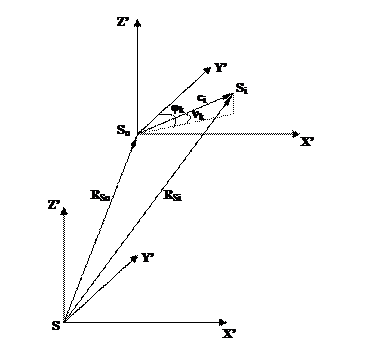
На рис. 3 показаны система координат сканера SX’Y’Z’, в которой производится определение координат точек объекта М, и система координаткамеры Sixyz,которая может изменять свое положение и ориентацию относительно системы координат сканера во время съемки. Наша задача найти координаты вектора r в системе координат камеры с тем, чтобы по ним взять со снимка соответствующую плотность d изображения точки M. Из этого рисунка следует, что
R = RM - RSi (2) или NAi r = RM - RSi (3)
Где N – скаляр; Аi – матрица поворота системы координат камеры в момент съемки i относительно система координат сканера; r – вектор, определяющий положение точки m в системе координат камеры; RM -вектор, определяющий положение точки M в системе координат сканера; RSi – вектор, определяющий положение начала системы координат камеры относительно ситемы координат сканера в момент съемки i.
Рис.3
Из (3) имеем:
или в координатной форме:
Если выразить из третьего уравнения выражения (5) значение 1/N и подставить в первые два, то получим известные в фотограмметрии уравнения коллинеарности:
В этих уравнениях известны все величины, необходимые для вычисления координат x,y. Так, координаты точки объекта X’Y’Z’ вычисляются по (1), а элементы внешнего ориентирования снимка следующим образом. Как следует из рис.4, вектор RSi, определяющий положение центра проекции камеры Si в момент фотографирования i в системе координат сканера SX’Y’Z’ равен:
где RSo – вектор, определяющий положение точки вращения камеры в системе координат сканера; ci – вектор, задающий положение центра проекции камеры Si в системе координат SoX’Y’Z’, параллельной системе координат сканера SX’Y’Z’.
Рис.4 В координатной форме уравнение (7) имеет вид:
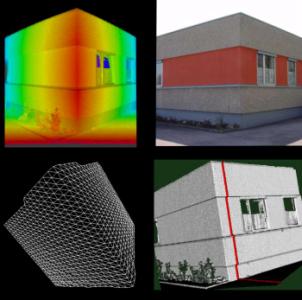
где, с – модуль вектора ci (величина постоянная для данного сканера и камеры), jk, nk – горизонтальный и вертикальный углы наклона камеры (задаются и измеряются сканером - величины кратные соответствующим углам поля зрения камеры). Величины XSo,YSo,ZSo,c являются постоянными для данного сканера и определяются в результате его калибровки. Направляющие косинусы aij в (6) вычисляются по известным формулам, подставляя в них вместо α,ω соответствующие значения jk, nk. При этом κ = 0. В результате для каждой точки объекта с координатами X’Y’Z’ получается плотность изображения d, взятая со снимка по координатам xy, вычисленным по (6). Теперь трехмерную модель можно визуализировать в естественных или псевдоцветах (рис.7,8,10) под различными углами зрения с целью ее измерения (векторизации элементов объекта, определения объемов, площадей и т.д.). Кроме того модель можно представить в виде триангуляции Делоне.
Рис.7
Рис.8
Подвижные сканерные системы. Подвижные сканерные системы предназначены для съемки протяженных объектов, таких как улицы городов, тоннели, береговая линия и т.д. На рис.9 показаны некоторые примеры подвижных сканерных систем.
Рис.9
Подвижная сканерная система состоит из одного или нескольких сканеров, GPS – приемника и инерциальной геодезической системы INS. Все эти элементы жестко закреплены на платформе, которая устанавливается на носитель (автомобиль, катер и др.).
Очевидно, что во время сканирования положение и ориентация самого сканера (системы координат сканера SX’Y’Z’) будут непрерывно изменяться за счет движения носителя, т.е. в каждый момент времени у сканера будут свои элементы внешнего ориентирования. Для определения этих элементов и служат GPS-приемник (определяет линейные элементы внешнего ориентирования сканера XSYSZS) и инерциальная система INS (определяет угловые элементы внешнего ориентирования сканера αωκ и линейные совместно с GPS), входящие в комплект подвижной сканерной системы. Кроме того, для точного определения координат точек объекта в системе координат объекта необходимо знать взаимное положение всех элементов системы (GPS, INS и сканера), которое определяется в результате калибровки системы.
Рис.10
SX’Y’Z’ – система координат сканера, в которой определяется положение точки объекта М (вектор R);
Таким образом, вектор
(10) В координатной форме это уравнение можно записать так:
Здесь XGPSYGPSZGPS – координаты центра антенны GPS- приемника, которые измеряются с помощью этого приемника;
В уравнениях (11) величины
На рис.11 показаны примеры съемок, выполненных подвижной сканерной системой.
Рис.11
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.216 (0.008 с.) |



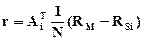 (4)
(4)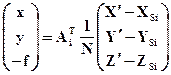 (5)
(5)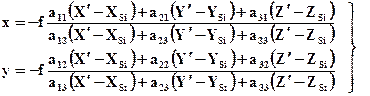 (6)
(6)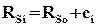 (7)
(7)
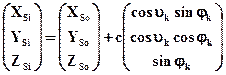 (8)
(8)






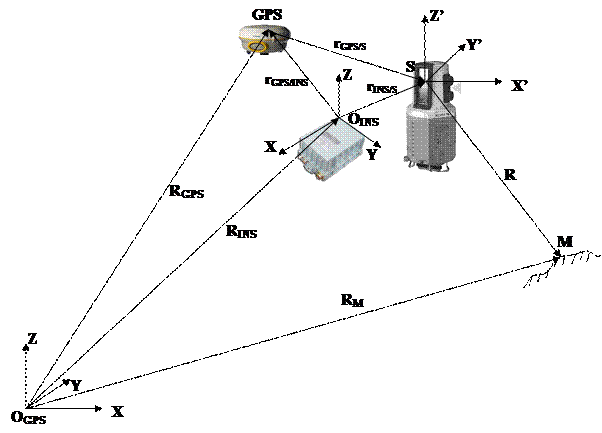 Получим формулы для вычисления координат точек объекта, по результатам съемки с помощью подвижной сканерной системы. Для этого рассмотрим рис.10.
Получим формулы для вычисления координат точек объекта, по результатам съемки с помощью подвижной сканерной системы. Для этого рассмотрим рис.10.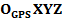 -система координат объекта, в которой измеряется положение антенны GPS (вектор
-система координат объекта, в которой измеряется положение антенны GPS (вектор 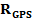 );
);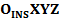 – система координат инерциальной навигационной системы, в которой определяются в результате калибровки всей съемочной системы вектора
– система координат инерциальной навигационной системы, в которой определяются в результате калибровки всей съемочной системы вектора 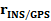 ,
, 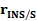 и
и 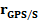 задающие взаимное положение инерциальной системы, сканера и антенны GPS.
задающие взаимное положение инерциальной системы, сканера и антенны GPS.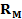 , определяющий положение точки М объекта в системе координат объекта можно получить, как следует из рис.10, по следующей формуле:
, определяющий положение точки М объекта в системе координат объекта можно получить, как следует из рис.10, по следующей формуле: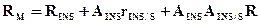 (9)
(9)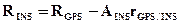 где
где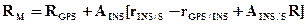 тогда
тогда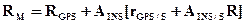 Окончательно получим:
Окончательно получим: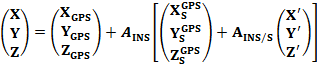 , (11)
, (11)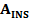 – матрица поворота, которая вычисляется по трем углам αωκ, измеряемым инерциальной системой, т.е. эта матрица определяет угловую ориентацию системы координат
– матрица поворота, которая вычисляется по трем углам αωκ, измеряемым инерциальной системой, т.е. эта матрица определяет угловую ориентацию системы координат 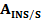 - матрица поворота, определяющая взаимную угловую ориентацию (углы ∆α,∆ω,∆κ) системы координат сканера SX’Y’Z’ и системы координат инерциальной навигационной системы
- матрица поворота, определяющая взаимную угловую ориентацию (углы ∆α,∆ω,∆κ) системы координат сканера SX’Y’Z’ и системы координат инерциальной навигационной системы 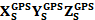 – координаты вектора
– координаты вектора 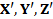 - измеренныекоординаты точки объекта в системе координат сканера.
- измеренныекоординаты точки объекта в системе координат сканера.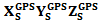 и
и 



