
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторение теоретического материалаСодержание книги Поиск на нашем сайте
«Вы уже накопили некоторый опыт нахождения производной. И сегодня мы посмотрим, чему же вы научились. Повторим теоретический материал». 2 ученика идут к доске выписывать известные им правила нахождения производной. В это время класс отвечает на вопросы учителя: а) что такое производная? б) какие смыслы производной существуют? в) что такое производная с геометрической точки зрения? г) какой угол образует прямая с осью абсцисс: · если k>0 · если k<0 · если k=0 если прямые a || в? д) что такое производная с механической точки зрения? е) что значит продифференцировать? ж) какая функция называется дифференцируемой в точке з) что такое критические точки? и) какую формулу имеет уравнение касательной? Применение теоретического материала к решению задач «Рассмотрев теоретический материал вычисления производной, применим его при решении задач». В это время на интерактивной доске высвечиваются примеры для устного нахождения производной (отвечают все учащиеся класса по цепочке). Найдите производную функции
После решения этих примеров на интерактивной доске высвечивается следующее задание для устного счета. Учащиеся выходят по одному к доске и стрелками устанавливают соответствие между левым и правым столбцами таблицы. Установите соответствие
Далее на интерактивной доске высвечиваются следующие задания для устного счета. Учащиеся выходят по одному к доске для их выполнения.
«Проведем контроль усвоенного материала. Для этого на листе бумаги, лежащем на краю стола, необходимо решить примеры, которые высветятся на интерактивной доске (два варианта). При этом, решив примеры варианта, нужно указать на листе его номер, номер примера, и, найдя в таблице (интерактивная доска) классификатор правильного ответа (1-4), указать его код. Таким образом, в итоге на листе в качестве ответов должен быть отображен номер варианта и столбец из ответов – а) 2 б) 4 и т.д. На выполнение задание дается 5 минут» В это время на интерактивной доске отображается задание программированного контроля и таблица с вариантами ответа. В данном уроке запланировано проведение трех последовательных самостоятельных работ по системе программированного контроля. Найти производную функции. Программированный контроль. Самостоятельная работа №1
Варианты ответов
После выполнения учащимися каждого задания программированного контроля ученики в паре обмениваются листами. Учитель сообщает коды правильных ответов, и учащиеся делают соответствующие пометки на листе партнера по паре. Один заранее выбранный ученик (успевающий в предмете) собирает все листы и выставляет в заранее подготовленную сводную ведомость отметки по ранее обозначенным критериям. Наиболее типичные неверные решения разбираются на доске учащимися, верно решившими пример. По этому же алогритму работы проводятся и последующие 2 самостоятельных работы. Самостоятельная работа №2
Варианты ответов
Самостоятельная работа №3
Варианты ответов
«Повторим геометрический смысл производной». На интерактивной доске появляются задания. Один ученик решает на интерактивной доске, двое – на боковых досках (все решают один пример).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.107 (0.006 с.) |

 ?
?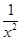 +5
+5

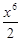

 )
)


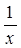
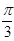 -2x)
-2x)
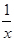
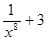


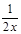
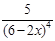
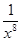 +2
+2



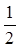
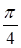 )
)
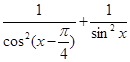
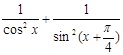
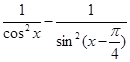
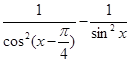
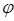 (x)=7+x
(x)=7+x 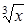 ,
, 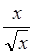 ,
, 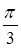 )-?
)-?
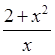 , h `(-1)-?
, h `(-1)-?
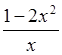 , h `(-1)-?
, h `(-1)-?
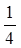

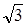
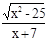 , D(f)-?
, D(f)-?
 , D(f)-?
, D(f)-?
 ,
, 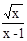
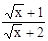 ,
, 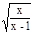
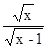 ,
, 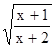
 ,
, 



