
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругая деформация подшипниковСодержание книги
Поиск на нашем сайте
8.3.1. Подшипник скольжения. Упругое сжатие
где h2 - высота вкладыша подшипника (см. рис. 4.1,а); F - горизонтальная проекция площади соприкосновения вкладыша с подушкой, которую ориентировочно можно рассчитать, как Для двух подшипников скольжения (верхнего и нижнего) получим
8.3.2. Подшипник качения. Упругую деформацию одного подшипника качения рассчитывают по формуле [4]
где n - число рядов роликов в подшипнике; z - число роликов в одном ряду; Упругая деформация двух подшипников качения
8.3.3. Подшипник жидкостного трения. Для расчета величины упругой деформации подшипника жидкостного трения (ПЖТ) можно воспользоваться приближенной формулой [1]:
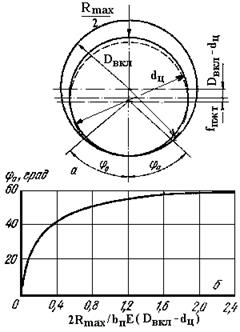
Рис. 8.1. Схема деформации ПЖТ (а) и график изменения параметра Величина диаметрального зазора в подшипнике
Упругая деформация двух подшипников ПЖТ
8.4. Упругая деформация нажимного устройства
Общую упругую деформацию винтовой пары (см. рис. 5.1)
где Величину
где Деформация тела винта на участке между пятой и гайкой равна (см. рис. 5.1):
где
Упругая деформация станины
8.5.1. Станины закрытого типа (см. рис. 7.1). Общая деформация станины в вертикальном направлении равна
где Составляющие 8.5.1.1. Для станины со скругленными углами радиусом r (см. рис. 7.3,б)
где Е и G - соответственно, модуль упругости и модуль сдвига материала станины,
8.5.1.2. Для станины, имеющей прямоугольную форму (r =0, см. рис. 7.3,а),
8.5.1.3. Для станины, имеющей скругленные поперечины (
а удлинение стоек В формулах (8.25)-(8.32) принято: 8.5.2. Станины открытого типа (см. рис. 7.5 и 7.8). Деформация станины открытого типа определяется количеством валков в рабочей клети и способом крепления крышки станины. 8.5.2.1. Общая деформация станин открытого типа клетей дуо равна
где Составляющие
где f1 и f2 - рассчитывают в зависимости от формы станины соответственно по формулам (8.25) и (8.26), (8.28) и (8.29) или (8.31) и (8.32). При этом величина изгибающего момента принимается Удлинение стоек Упругую деформацию крышки станины с достаточной точностью можно рассчитать по формуле
где Упругое растяжение стяжных болтов определяют по закону Гука
где а сжатие крепежных клиньев по формуле
где S и В - соответственно длина и ширина крепежного клина (см. рис. 7.5,б); 8.5.2.2. Деформация станин открытого типа рабочих клетей трио зависит от способа крепления среднего валка (рис. 8.2) и от того, в каком горизонте ведется прокатка. При клиновом способе крепления (см. рис.8.2,а) и при прокатке в нижнем горизонте деформацию станины можно определить по уравнению:
где
где а и в - соответственно ширина и высота прилива станины (см. рис. 7.9); В2 - толщина стойки станины. При прокатке в верхнем горизонте, деформация станины будет определяться уравнением:
Рис. 8.2. Способы крепления среднего
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 подшипника скольжения открытого типа под действием реакции усилия прокатки
подшипника скольжения открытого типа под действием реакции усилия прокатки  может быть определена по формуле
может быть определена по формуле (8.13)
(8.13) ; Е - модуль упругости материала вкладыша, принимаемый для вкладыша из текстолита (0.06¸0.10)×10 5 МПа [6].
; Е - модуль упругости материала вкладыша, принимаемый для вкладыша из текстолита (0.06¸0.10)×10 5 МПа [6]. . (8.14)
. (8.14) (8.15)
(8.15) - диаметр ролика.
- диаметр ролика. (8.16)
(8.16)
 , (8.17)
, (8.17) и
и  - соответственно диаметры вкладыша и цапфы ПЖТ; j0 - угловая ширина половины площадки контакта цапфы ПЖТ с вкладышем, град. (рис. 8.1,а)
Значение
- соответственно диаметры вкладыша и цапфы ПЖТ; j0 - угловая ширина половины площадки контакта цапфы ПЖТ с вкладышем, град. (рис. 8.1,а)
Значение  определяют по графику на рис. 8.1,б в зависимости от величины соотношения
определяют по графику на рис. 8.1,б в зависимости от величины соотношения  , где
, где  - ширина подушки подшипника; Е - среднее значение модуля упругости материала цапфы
- ширина подушки подшипника; Е - среднее значение модуля упругости материала цапфы  и вкладыша подшипника
и вкладыша подшипника  , т.е.
, т.е. 
 может быть принята по рекомендациям [.7.]:
может быть принята по рекомендациям [.7.]: =(0.02¸0.07)×
=(0.02¸0.07)×  (8.18)
(8.18) (8.19)
(8.19) от действия усилия
от действия усилия  на шейку валка определяют по уравнению[1]:
на шейку валка определяют по уравнению[1]: , (8.20)
, (8.20) - упругая деформация тела и резьбы гайки;
- упругая деформация тела и резьбы гайки;  - упругая деформация тела винта на участке между пятой и гайкой; коэффициент 1.1 учитывает упругое сжатие подпятника нажимного винта.
- упругая деформация тела винта на участке между пятой и гайкой; коэффициент 1.1 учитывает упругое сжатие подпятника нажимного винта. (8.21)
(8.21) - высота гайки;
- высота гайки;  - внешний диаметр гайки; d - внутренний диаметр резьбы гайки;
- внешний диаметр гайки; d - внутренний диаметр резьбы гайки;  - модуль упругости материала гайки, который можно принимать для бронзовой гайки (1.0¸1.15)105 МПа.
- модуль упругости материала гайки, который можно принимать для бронзовой гайки (1.0¸1.15)105 МПа. (8.22)
(8.22) - высота сжимаемой части нажимного винта;
- высота сжимаемой части нажимного винта;  - диаметр винта;
- диаметр винта;  - модуль упругости материала нажимного винта.
- модуль упругости материала нажимного винта. (8.24)
(8.24) - упругий прогиб двух поперечин от действия изгибающих моментов;
- упругий прогиб двух поперечин от действия изгибающих моментов;  - деформация поперечин от действия поперечных сил;
- деформация поперечин от действия поперечных сил;  - удлинение стоек от действия продольных сил.
- удлинение стоек от действия продольных сил.
 , (8.25)
, (8.25) (8.26)
(8.26) (8.27)
(8.27) (8.28)
(8.28) (8.29)
(8.29) (8.30)
(8.30) см.рис. 7.3,в),
см.рис. 7.3,в), (8.31)
(8.31) (8.32)
(8.32) рассчитывают по формуле (8.27) при
рассчитывают по формуле (8.27) при  .
. и
и  , а необходимые для расчетов значения моментов инерции поперечных сечений станины
, а необходимые для расчетов значения моментов инерции поперечных сечений станины  ,
,  ,
, 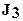 и
и  , площади этих сечений
, площади этих сечений  ,
,  ,
, 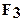 и
и  , расстояния между нейтральными линиями поперечин и стоек
, расстояния между нейтральными линиями поперечин и стоек  и
и  , а также статически неопределимый изгибающий момент
, а также статически неопределимый изгибающий момент  определяют в соответствии с рекомендациями раздела 7.1.
определяют в соответствии с рекомендациями раздела 7.1.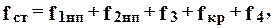 (8.33)
(8.33) и
и 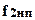 - упругая деформация нижней поперечины станины от действия соответственно изгибающих моментов и поперечных сил;
- упругая деформация нижней поперечины станины от действия соответственно изгибающих моментов и поперечных сил;  - удлинение стоек;
- удлинение стоек;  - упругая деформация крышки станины;
- упругая деформация крышки станины;  - упругое растяжение болтов (см. рис. 7.5,а) или сжатия крепежных клиньев (см. рис. 7.5,б).
- упругое растяжение болтов (см. рис. 7.5,а) или сжатия крепежных клиньев (см. рис. 7.5,б). ,
,  , (8.34)
, (8.34) , где Т - сила защемления подушек, которую рассчитывают по формуле (7.31), С - расстояние от нейтральной линии нижней поперечины до подушки верхнего валка (см. раздел 7.2 и рис. 7.6). Параметры
, где Т - сила защемления подушек, которую рассчитывают по формуле (7.31), С - расстояние от нейтральной линии нижней поперечины до подушки верхнего валка (см. раздел 7.2 и рис. 7.6). Параметры  и
и  ,
,  и
и  ,
,  определяют для нижней поперечины по методике, изложенной в разделе 7.1.
определяют для нижней поперечины по методике, изложенной в разделе 7.1. равной расстоянию от нейтральной линии нижней поперечины до оси крепления стяжного болта (см. рис. 7.5,а) или до центра верхней поверхности крепежного клина (см. рис. 7.5,б).
равной расстоянию от нейтральной линии нижней поперечины до оси крепления стяжного болта (см. рис. 7.5,а) или до центра верхней поверхности крепежного клина (см. рис. 7.5,б). , (8.35)
, (8.35) - расстояние между осями крепежных болтов или клиньев;
- расстояние между осями крепежных болтов или клиньев;  (8.36)
(8.36) длина деформируемой части болта (см. рис. 7.5,а);
длина деформируемой части болта (см. рис. 7.5,а);  - площадь поперечного сечения болта; Еб - модуль упругости материала болта,
- площадь поперечного сечения болта; Еб - модуль упругости материала болта, (8.37)
(8.37) - толщина стойки станины; Ек - модуль упругости материала клина.
- толщина стойки станины; Ек - модуль упругости материала клина.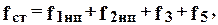 (8.38)
(8.38) - упругий прогиб нижней поперечины станины от действия изгибающих моментов и поперечных сил;
- упругий прогиб нижней поперечины станины от действия изгибающих моментов и поперечных сил;  - упругая деформация выступов станины. Составляющие
- упругая деформация выступов станины. Составляющие  равной расстоянию от нейтральной линии нижней поперечины до верхнего выступа (т.е.
равной расстоянию от нейтральной линии нижней поперечины до верхнего выступа (т.е.  (8.39)
(8.39) (8.40)
(8.40) - деформация крышки станины, рассчитываемая по формуле (8.35);
- деформация крышки станины, рассчитываемая по формуле (8.35);  - деформация стяжных болтов или крепежных клиньев, рассчитываемая соответственно по формуле (8.36) или (8.37);
- деформация стяжных болтов или крепежных клиньев, рассчитываемая соответственно по формуле (8.36) или (8.37);




