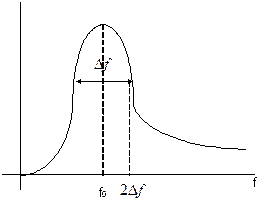Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормирование метрологических характеристикСодержание книги Поиск на нашем сайте
Норма – результат соглашения между потребителем и изготовителем. Нормирование –регламентация того факта, каким должен быть прибор.
Что нормируется? - Все характеристики, влияющие на точность полученного результата измерения 7. характеристики, с помощью которых определяется результат измерений - функции преобразования - шкала деления - количество разрядов кода - единица последнего разряда кода 8. чувствительность влияющих факторов 9. погрешности 10. характеристики связи средства измерения с объектом и нагрузкой 11. динамические характеристики 12. неинформативные параметры
ПРИМЕР: Сигнал Ели Ели Ели
Нормирование погрешностей: III. нормируются вероятностные характеристики погрешности IV. нормируются предельные значения погрешностей:
Нормирование предельного значения погрешности: 4. - -
5. - - 6. -
Для измерительных приборов вводится понятие класс точности – величина, численно равная максимальному значению К - класс точности. 3.
3. приборы, у которых нормируется  : :
Пример:
Структурные схемы измерения 4. прямого преобразования 5. компенсационного преобразования 5.1 с астатической характеристикой 5.2 со статической характеристикой 6. с автоматической коррекцией погрешности 1.Структурные схемы измерения прямого преобразования
Функции преобразования отдельных блоков могут быть линейными и нелинейными. Пусть все функции линейные:
Функции преобразования: Возникают погрешности: 3.
Идеальный случай: Хп=КХ при всех Реальный случай:
При последовательном включении блоков их число ограничено. Можно подобрать блоки с различным
4.
ПРИМЕР:
При наличие помехи, первый каскад нужно делать очень тщательно (экранирование, заземление, использование качественных кабелей). Фильтры не всегда помогают, так как они влияют на динамику.
4. Структурные схемы измерения компенсационного преобразования
4.1 Структурные схемы измерения компенсационного преобразования с астатической характеристикой
S=
Чтобы реализовать такой режим работы, в любом месте цепи прямого преобразования должно стоять запоминающее интегрирующее звено.
В связи с тем, что современные интегрирующие устройства обладают невысокой чувствительностью, то обычно их ставят в конце цепи. Возникают погрешности: 1.
Цепь отрицательной обратной связи выполняется на пассивных элементах
2. внутренние дрейфы порог чувствительности интегратора Будем считать, что помехи воздействуют на цепь прямого преобразования, так как цепь обратной связи низкоомная. Приведем помехи на вход:
Введение отрицательной обратной связи
4.2 Структурные схемы измерения компенсационного преобразования со статической характеристикой
bK-петлевое усиление.
Возникают погрешности: 2.
3. при больших Kb, 4. При больших Kb, замкнутая система может потерять устойчивость, т.е система будет реагировать не на сигнал, а на внутренние флуктуации
Компромисс между точностью и устойчивостью может быть найден при:
2.
Введение отрицательной обратной связи не уменьшает аддитивную погрешность.
Теория Погрешностей 5. причины появления погрешностей результата измерений 6. погрешности систематические и случайные, описание случайных погрешностей 7. идеи суммирования погрешностей 8. обработка ряда прямых наблюдений для получения результатов измерений
2. причины появления погрешностей результата измерений
схема измерения эксперимента
Результат нужен для того, чтобы иметь однозначную информацию об измеряемой величине. Погрешность результата измерений: Хр – истинное значение Хn – результат измерений
Причины: -погрешность метода ПРИМЕР: Объект измерений – генератор А) модель
V-вольтметр, измеряющий действующее значение
Б) реально:
если если не не учитывается, что сигнал отличается от синусоидального
- инструментальная погрешность (ею обладает средство измерения) - погрешность от влияния средства измерения на объект измерения. ПРИМЕР:
Есть 3 амперметра:
- погрешность человека-экпериментатора - погрешность, связанная с ЭВМ (погрешность округления)
2. погрешности систематические и случайные, описание случайных погрешностей Погрешность результата формируется под воздействием факторов: III. факторы, которые в процессе измерения остаются постоянными или меняются по закону, следовательно, формируются систематические погрешности IV. факторы, которые в процессе измерения меняются случайным образом с интенсивностью, которую трудно предсказать, следовательно, формируются случайные погрешности
ПРИМЕР 1:
можно свести
ПРИМЕР 2:
ПРИМЕР 3:
Если
Как свести Методы: 4. правильная постановка эксперимента.
5. введение поправочных кривых, графиков и т.д 6. специальные методы ПРИМЕР:
Случайная величина полностью описывается законами распределения интегрирующими и дифференцирующими (плотностью распределения вероятности). На практике – дифференцирующими законами. ПРИМЕР:
Известен дифференцирующий закон распределения, следовательно, можно найти вероятность того факта, что измеряемая величина находится между Х1 и Х2.
Во многих случаях измеряемая величина распределяется около истинного значения Q (но не всегда). Плотность распределения погрешностей:
ПРИМЕР:
Как с помощью вероятностных характеристик оценить погрешность? Оценку погрешности производят с помощью доверительных интервалов и доверительной погрешности:
k- коэффициент, зависящий от р(х) и Рдов
3. идеи суммирования погрешностей
3. первый подход 4. второй подход: суммируются погрешности на основании вероятностных характеристик
5. если законы распределения не Гауссов, то при n>3 возникают сложности 6. может возникать трансформация закона суммарного распределения. ПРИМЕР:
На практике существует только 2 значения доверительной вероятности.
ПРИМЕР:
r-коэффициент корреляции (коэффициент связи)
r = 0 – некоррелированы
На практике:
ПРИМЕР:
Примечание: При суммирование погрешностей обычно аддитивные и мультипликативные составляющие суммируются отдельно друг от друга.
4. обработка ряда прямых наблюдений для получения результатов измерений Обработка результатов предполагает, что одну и ту же величину измеряют много раз в одинаковых условиях. Х - измеряемая величина n>40 – количество измерений Из ряд наблюдений нужно исключить промахи (по определенным методам). Ранжирование: Хmin … Xmax Ищем оценки числовых параметров: 1). оценка математического ожидания
2). оценка СКО:
3). найти закон распределения:
4. 5. из всех n находим частоту попадания на интервал 3.
7. По виду гистограммы выдвигается гипотеза, какому закону распределения она соответствует. 8. Критерий согласия: например, Для подсказки в измерительной технике говорится, какие законы распределения наиболее используются:
4).
Примечание: Существуют случаи, когда не нужно строить гистограмму для определенного закона распределения: - когда имеются статистические данные - когда закон распределения уже известен - если результат измерений формируется под действием большого числа независимых факторов, причем вклад каждого фактора в результат одинаков, то можно считать, что закон нормальный (N>5). - Если закон распределения нормальный, а n>10, то можно пользоваться распределением Стьюдента:
ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ 13. структурная схема электромеханических приборов (с элементами классификации) 14. моменты, действующие в приборах 15. магнитоэлектрические измерительные приборы 16. магнитоэлектрический амперметр и вольтметр 17. магнитоэлектрический омметр 18. магнитоэлектрический гальванометр 19. баллистический гальванометр (применение для измерения магнитного потока) 20. электродинамические измерительные механизмы 21. электродинамический амперметр и вольтметр 22. электродинамический ваттметр 23. индукционный измерительный механизм 24. индукционный счетчик энергии 1. структурная схема электромеханических приборов (с элементами классификации)
Риц, Рим, Роу – параметры ИЦ, ИМ, ОУ
коррекции (обычно в ИЦ) 2. моменты, действующие в приборах 4) вращательный момент магнит возникает и тянет подвижную часть слева направо.
Так как подвижная часть обладает большой массой, то реагирует не на мгновенное значение, а на среднее.
5) противодействующий момент Мпр (искусственный) Мпр действует слева направо. Его можно создать механическим или электрическим путем.
Существует устойчивое положение равновесия, когда:
ПРИМЕР:
Получаются однозначные показания, т.е. каждому значению измеряемой величины соответствует одно показание.
Муст=Мвр-Мпр устанавливающий момент, который возникает сам, если:
Если прибор находится в состоянии равновесия, а его выводят из этого состояния, то появляется Муст.
6) Момент успокоения, возникающий в динамике
6. магнитоэлектрические измерительные приборы
3) с механическим противодействующим моментом прибор с подвижной рамкой:
ПН – полюсные наконечники. С - сердечник. ПР – подвижная рамка.
Через рамку пропускается переменный или постоянный ток на низкой частоте. Рамка находится в магнитном поле индукции В. Форма ПН и С сделана так, что в зазоре обеспечивается радиальное, равномерное, постоянное поле индукции В. ПН и С – из магнитномягкого материала. N и S - из магнитотвердого материала.
Особенности: 3. 4. прибор полярный
4) Логометр
Поверхности не цилиндрические.
Прибор для измерения соотношения токов.
4. магнитоэлектрические амперметры и вольтметры АМПЕРМЕТР
Надо доказать, что схема миллиамперметра обладает температурной погрешностью, т.е.
Схема термокомпенсации:
Rт – термистр Rm – манганиновое сопротивление
Многопредельный прибор: R доб – добавочное сопротивление, служит для компенсации термопогрешности Rш1, Rш2, Rш3 – сопротивление шунтов, рассчитанных на разные пределы I1>I2>I3
ВОЛЬТМЕТР
Электродинамический вольтметр
α = 1/w*Iнк*Iпк*cos(Iнк^Iпк)*dM/dα
Iнк=Iпк= Откуда: α = F1(U), но так же α = F1(w) Емкость служит для уменьшения частотной погрешности
Если подобрать С, то можно уменьшить частично погрешность.
10)Электромеханический ваттметр
Iн = Iнк
α = 1/w*Iнк*Iпк*cos(Iнк^Iпк)*dM/dα P=Iн*U*cosφ
Iнк = Iн => Iпк = U/R
ð α = 1/w*Iн*U/R*cos(φ - γ)*dM/dα
Шкала равномерная, если dM/dα (т.к. α прямо пропорциональна cosφ) Примечание Самые высокоточные приборы, но на них влияют магнитные поля => они все экранированы 11)Принцип действия индукционного измерительного механизма Обозначение:
Для создания момента вращения необходимо иметь не менее 2 переменных магнитных потоков, сдвинутых в пространстве и во времени.
M1,M2 –магнитопровода, потоки Ф1t и Ф2t пронизывают диск; они сдвинуты относительно токов на α. Токи сдвинуты относительно друг друга на φ. φ – потери.E1,E2 – ЭДС
ЭДС => в Al возникают вихревые токи
Mврt = Mврt1 + Mврt2 Эти моменты возникают из-за взаимодействия вихревого тока и переменного магнитного потока Mврt = Ф1t* i22 +Ф2t* i11 Т.к подвижная часть обладает большим моментом инерциии то она реагирует на среднее значение. Mвр = 1/To*∫Mврtdt = Ф1*I22*cos(Ф1^I22) + Ф2*I11*cos(Ф2^I11) cos(Ф1^I22) = cos(90 + φ) = -sinφ cos(Ф2^Iн) = cos(90 - φ) = sinφ Вихревой ток всегда пропорционален частоте и потоку, который его вызвал I22 = cfФ2,Iн = cfФ1 => Mвр = сf[-Ф1Ф2sinφ + Ф1Ф2sinφ] = сf(Ф1Ф2sinφ) знак “-” чисто математический
12)Однофазный индукционный счетчик энергии Предназначен для измерения энергии: W=P*t => накопление энергии со временем,т.к. прибор интегрирующий
Части прибора: 1)измерительный механизм (п.11) 2)счетное устройство(число оборотов счетчика n)
W=Cном*N => W=Д*N
Сном-номинальная постоянная счетчика Для каждого счетчика есть действительная постоянная счетчика Cд ≠ Сн, но Cном ≈ Сдс погрешностью 0.2 (класс 0.2)
ТО – токовая обмотка ОН – обмотка напряжения *-генераторные концы:начало обмотки
Iн = Iо Iон ≈ U/w*Loн ОН – имеет большое количество витков => большая индуктивность Mвр = c*Ф1Ф2sin(Ф1^Ф2) P=U*Iон*cosφ Надо Mвр = P
Надо: sin(Ф1^Ф2) = sin[β –αI - φ] Если β = 90, то sin(Ф1^Ф2) = cos(φ)
Mт – тормозной момент; cсоздается за счет взаимодействия поля специального тормозного момента с вихревыми токами,наводимыми при его вращении Mт = k*dα/dt Mвр = Мт => k1p = k*dα/dt (**)
=> W = Cном*N Cном = k/k1
Электронные приборы.
1.Общие сведения об электронных приборах 2.электронные вольтметры постоянного тока 3. электронные вольтметры переменного тока 4.комбинированный электронный вольтметр 5.селективный вольтметр 6. электронный веберметр 7. электронный милиомметр
1.см. все первые лекции
Обладают сравнительно невысокой точностью, т.е. нужно смотреть паспорт. Чаще всего нужно комбинировать и устанавливать 0 (см. усилители) современные приборы обладают высокой точностью. Выпуск на микросхемах и с микропроцессорами
2)электронный вольтметр постоянного тока
Схема1:без преобразования спектра Схема2:c преобразованием спектра
Схема1:
измеряет мВ и выше УПТ- усилитель постоянного тока ППИ – переключатель пределов измерений(делитель) (чаще всего двух шкальный) Отсчет производится с м/э им
Применение двухшкального прибора позволяет уменьшить γ Tок(=) => нет преобразования спектра
УПТ=>не менее 10мВ,т.к. есть Uдр
Схема2:
Многошкальный,многопредельный
М-модулятор – преобразует постоянное U в переменное; выходной сигнал обычно – меандр(если на микросхеме).Если сигнал малый то используем вибропреобразование.
Для демодуляторов (или МДМ - схема)-преобр. переменное U в постоянное
СГ-синхронный генератор(опорный сигнал) ППИ-переключатель пределов измерений Есть преобразование по частоте => преобразование спектра Малые сигналы,т.к. усилитель переменного тока(нет Uдр)
3) электронные вольтметры переменного тока
U~
а)форма
б)частота f = от fmin до fmax в)амплитуда А = от Аmin до Аmax г)Umax? U? Ucр?
Частота
1)широкополосные вольтметры
низкая помехозащищенность fmin < fпом < fmax =>помеха усиливается
Все вольтметры In широкополосные
2)узкополосные
2Δf << fo fo-частота настройки большая помехозащищенность т.к. узкая полоса пропускания(которую можно подобрать)
Широкополосные вольтметры Схема1:выпрямитель-усилитель Схема2: усилитель-выпрямитель
Схема1:
другие функции можно получить Um,U,Uср(в зависимости от схемы)
“+”:обладает широким частотным диапазоном “-”:относительно низкая чувтвительность(сотни миливольт)
2.Усилитель-выпрямитель
двухшкальный прибор более чувствительный(мкВ), широкий частотный диапазон
3.Комбинированный универсальный вольтметр
Eo-образцовый источник R1,R2,R3-образцовые сопротивления Д-детектор,стоит в кабеле
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.19.29 (0.01 с.) |

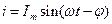
 -информативный параметр, то
-информативный параметр, то  - неинформативные параметры.
- неинформативные параметры. -информативный параметр, то
-информативный параметр, то 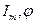 - неинформативные параметры.
- неинформативные параметры. -информативный параметр, то
-информативный параметр, то  - неинформативные параметры.
- неинформативные параметры.
 :
: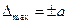

 :
:
 , где
, где  - конечное значение шкалы, х- текущее значение шкалы
- конечное значение шкалы, х- текущее значение шкалы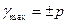
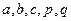 - числовые значения
- числовые значения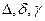 , а так же учитывающая характеристики, влияющие на точность измерений.
, а так же учитывающая характеристики, влияющие на точность измерений. приборы, у которых нормируется
приборы, у которых нормируется  2. приборы, у которых нормируется
2. приборы, у которых нормируется 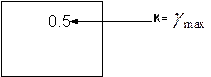

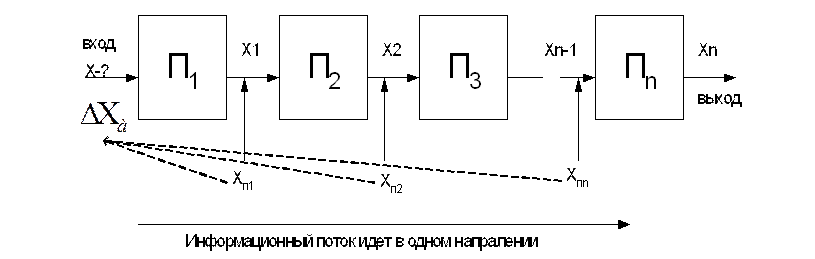 Найти: Хп=F(x) – функция всего устройства в целом.
Найти: Хп=F(x) – функция всего устройства в целом.
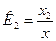 …
… 
 , где
, где  (1)
(1)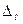 ←
←  ←
← 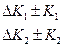 ←влияние внешних факторах
←влияние внешних факторах 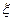

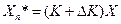 при всех
при всех 

 ←внешние помехи и внутренние дрейфы←Хп
←внешние помехи и внутренние дрейфы←Хп
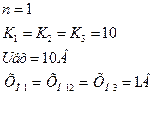


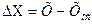
 =0
=0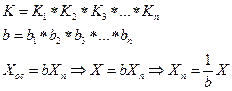 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент преобразования всего устройства
- коэффициент преобразования всего устройства
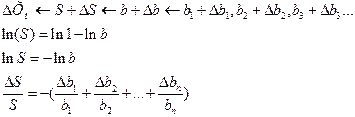
 ее можно сделать более стабильной
ее можно сделать более стабильной  .
.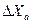 ←внешние помехи
←внешние помехи

 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент S зависит только от b и K.
- коэффициент S зависит только от b и K.
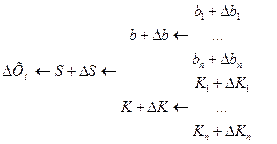



 , т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи
, т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи 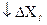 .
.

 вешние помехи, внутренние дрейфы→Хп
вешние помехи, внутренние дрейфы→Хп



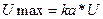
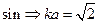


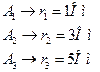
 , т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно.
, т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно. - истинное
- истинное

 , где
, где 
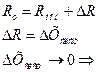
 к минимуму
к минимуму Делая многократные измерения одной и той же величины, можно получить (выявить)
Делая многократные измерения одной и той же величины, можно получить (выявить) 

 , тогда
, тогда  рассчитывается методами теории вероятности.
рассчитывается методами теории вероятности.




 На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
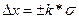
 - доверительный интервал
- доверительный интервал применяются такие значения в измерительной технике
применяются такие значения в измерительной технике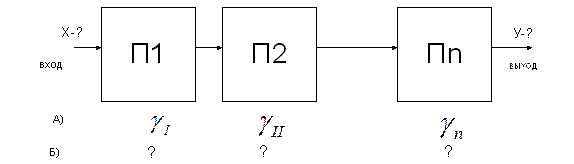



 при Рдов = …
при Рдов = … - суммарное СКО
- суммарное СКО
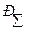 - суммарный закон распределения
- суммарный закон распределения
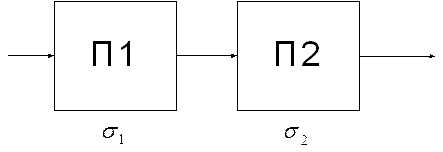

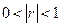
 - коррелированы (
- коррелированы ( )
)


 - ряд наблюдений
- ряд наблюдений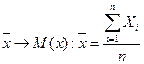

 гистограмма
гистограмма делится на нечетное число
делится на нечетное число






 - гарантия разброса относительно среднего с определенной вероятностью
- гарантия разброса относительно среднего с определенной вероятностью


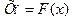 -однозначная функция
-однозначная функция нужно либо стабилизировать параметры, либо ввести схемы
нужно либо стабилизировать параметры, либо ввести схемы









 N,S – постоянные магниты.
N,S – постоянные магниты. - угол поворота.
- угол поворота.
 -чувствительность по току
-чувствительность по току



 Ip-ток рамки
Ip-ток рамки 


 , следовательно, с ростом температуры Ip уменьшается.
, следовательно, с ростом температуры Ip уменьшается.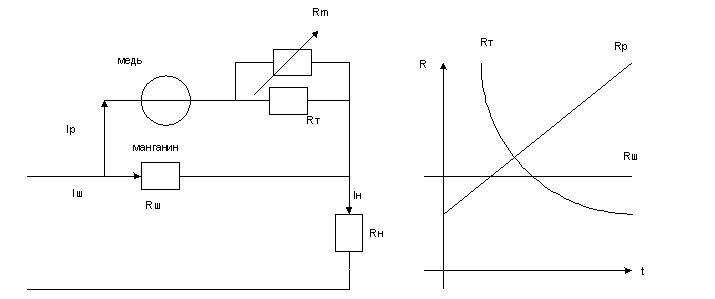


 температурная погрешность маленькая
температурная погрешность маленькая
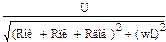 ; L = Lнк + Lпк
; L = Lнк + Lпк






 P=Iн*Uн*cosφ
P=Iн*Uн*cosφ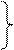
 Iпк =
Iпк = 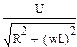 tg α = wL/r R= Rпк + Rдоб
tg α = wL/r R= Rпк + Rдоб Iпк = Ucosγ/R
Iпк = Ucosγ/R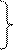 cos(φ - γ) = cos(Iнк^Iпк)
cos(φ - γ) = cos(Iнк^Iпк) Надо γ 0 => cos γ = 1 => cos(φ - γ) = cosφ => α = 1/w*Iн*U*cosφ*dM/dα
Надо γ 0 => cos γ = 1 => cos(φ - γ) = cosφ => α = 1/w*Iн*U*cosφ*dM/dα


 E1 i11
E1 i11


 Iто Фто ~ Iн
Iто Фто ~ Iн





 микровольты и меньше
микровольты и меньше