
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи курса. Понятие о стандартизации и сертификацииСодержание книги
Поиск на нашем сайте
Лекция 1
Лекция 2 Общее представление об измерениях. Понятие об измерении физической величины.
Физическое свойство Однако не всегда можно измерить физическое свойство. Физическое свойство – это свойство, присущее в качественном отношении многим предметам и объектам, но в количественном отношении индивидуально для каждого. Физические величины: 1) аналоговые; 2) дискретные (квантовые); 3) квази-детерминированные (неизвестны их параметры); 4) случайные. Измерить физическую величину – найти её значение опытным путём с помощью технических средств (в узаконенных единицах). СИ – стандарт CgSM – для физиков-теоретиков. Различают истинное значение физической величины и действительное. Истинное – идеально описывает физическую величину (его не возможно узнать) Действительное – полученное опытным путём, приближающееся к истинному, что его можно принимать за истинное. Под точностью измерений понимают близость результата измерений к истинному значению измеряемой величины. Обратная величина носит название погрешности. Погрешность – это разность между измерением и истинным значением. ΔX = Xизм – Xи = Xизм – Xд Xизм – значение измеряемой величины Xи – истинное значение Xд – действительное значение (получаем более точным прибором)
Для осуществления процесса измерения надо сравнить измеряемую величину с некой эталонной величиной, меняющейся в принципе. Тогда условие измерения имеет следующий вид: X = a[q] X – измеряемая величина a– количество единиц измерения, содержащиеся в X [q] – единица измерения Воспроизводимость – это качество измерений, отражающее близость друг к другу результатов измерений, выполненных в различных условиях в различное время, местах, разными средствами. Сходимость – качество измерений, отражающее близость друг к другу результатов измерений, проводимых в одинаковых условиях. На практике при исследовании сколь угодно сложного объекта приходится измерять определённые свойства (не все) – главные. При этом объекту приписывается модель. И эти модели менее сложные чем сам объект. Измерительный процесс можно рассматривать с точки зрения теории информации. Измерение – это уменьшение энтропии об объекте измерения. Какое количество информации мы можем получить в результате измерения?

При этом P(X) – это плотность вероятности После измерения.
 
     
 Xп – это приближенное значение. Xп – это приближенное значение.
На самом деле у нас 3А±Δ
 - это мера неопределённости ситуации, или энтропия. - это мера неопределённости ситуации, или энтропия.
Путём измерений получают сведения о количественных характеристиках свойств объектов. Такие сведения увеличивают наши знания и уменьшают степень неопределённости об объекте. Информация о значениях измеряемых физических величин называется измерительной. Сигнал, функционально связанный с измеряемой физической величиной, называют сигналом измерительной функции.
Лекция 3 Общие сведения об электрических измерениях и измерительной аппаратуре.
Классификация методов измерения.
I. 1) Непосредственное Одной природы X и Xo.
СУ обладает высокой чувствительностью (компараторы и другие). Опосредованное Х не имеет образцовой пары:
II. 3) Одновременное
Одновременное
III. 5) Нулевой О результате судят по совпадению отметки от измеряемой величины и от образцовой величины
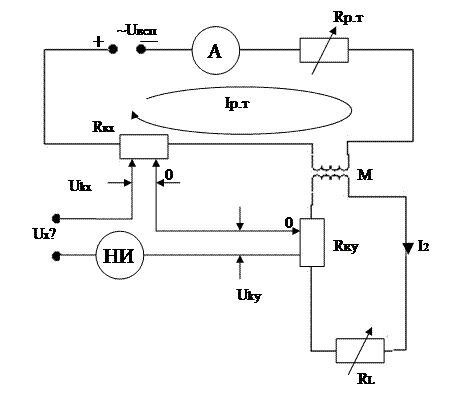
Пример 1. Потенциометр постоянного тока (компенсатор постоянного тока). Этот прибор служит для измерения с высокой точностью постоянного напряжения и единственный ум Eo – образцовое напряжение – это нормальный химический элемент и его ЭДС известно с высокой точностью. Rо – образцовое сопротивление. Известно с высокой точностью. Rк – образцовое высокоточное переменное сопротивление, чья шкала градуируется. Rр.т – переменное сопротивление для измерения рабочего тока. НИ – «нуль-индикатор». В его качестве используется высокочувствительный магнитоэлектрический гальванометр (до 1 положение переключателя: установка рабочего тока. 2 положение переключателя: измерение Ux. Работа схемы. 1) Переключатель в положение 1. Меняем Rр.т, пока ток через НИ не станет равным нулю (Iни = 0)
2) Переключатель в положение 2. Меняем Rк, пока ток через НИ не станет неравным нулю (Iни ≠ 0)
Когда переключаем переключатель в положение 2, тогда ток не идёт. Меряем чистую ЭДС без внутреннего сопротивления. Пример 2. Потенциометр переменного тока (компенсатор). Предназначен для измерения переменного напряжения с относительно высокой точностью по следующим причинам: здесь используется 2 метода (прямого измерения и сравнения). Метод прямого измерения применяется из-за того, что нету образцового источника. Рассмотрим 2-х координатный потенциометр:v
Идея: скомпенсировать.
Rкx, Rкy – высокоточные сопротивления. М – катушка взаимной индуктивности. Схема установки рабочего тока состоит из: вспомогательного напряжения Uвсп, амперметра, Rр.т. По амперметру выставляем Iр.т.
Есть ω. Следовательно должна быть поправка Попеременно изменяя Rкx и Rкy добиваемся на НИ в идеале нуля (в реале минимума).
Пример 3. Одинарный мост постоянного тока. Мостовые схемы имеют не менее 2 диагоналей.
Это 4-х плечий мост (R1,2,3,4 – плечи). Существует понятие равновесия моста. Iни = 0 (если ток через НИ равен нулю, то мост уравновешен) Пусть Iни = 0, если
Используется этот мост для измерения Rx с высокой точностью. Можно Rx подключить вместо R1234, как хотим.
R2 меняем пока ток Iни = 0 (мост в равновесии). Это будет когда
R2 здесь плечо сравнения. R3,4 – плечи сравнения. Rx ~10 Ом до
Когда уже Дифференциальный. Он менее точный чем нулевой, но более точный чем прямой. Пример 1.
Ux = 99 В ÷ 121 В а) прямой метод.
б) дифференциальный метод.
Пример 2. Неравновесный мост постоянного тока.
В точки с и d вставляем резистор где точно 1 кОм: Метод используется для отбраковки сопротивлений не равных номинальному. Метод совпадения. Используется, когда об измеряемой величине судят по совпадению отметки этой величины и образцовой. Пример: оптический пирометр. 1) Меняется сопротивление, из-за этого меняется ток и, следовательно, меняется температура нити накала. 2) Всё это происходит пока тело и нить накала не сравняются по цвету. Это значит, что температура нити накала равна искомой
Электронные приборы. Структурная схема
ЭС – электронная схема. ОУ – отсчетное устройство. Все электронные приборы имеют коаксиальные кабели для снижения помех.
Цифровые приборы.
Структурная схема
ВУ – входное устройство. АЦП – аналогово-цифровой преобразователь. ЦОУ – цифровое отсчетное устройство Аналого-дискретные приборы. Представляют собой совмещение электромеханического и цифрового прибора.
Измерительные приборы делятся на:
Пример: амперметр
Пример: самописец.
Пример: узкопрофильный прибор М1730.
При х<4 – нормальный режим. При х=4 значительно увеличивается освещенность фоторезистора, поэтому его сопротивление уменьшается. Происходит шунтирование схемы сопротивлением фоторезистора, вследствие происходит отключение чего-либо или срабатывает какая-либо система оповещения.
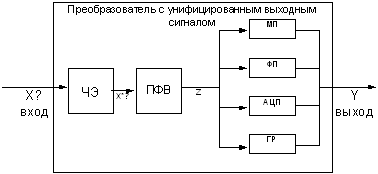
Преобразователи с унифицированным выходным сигналом (ПУВ).
Характеристики: 1) Вид сигнала: 2) Функция преобразования у(х)- линейная, возрастающая из нуля или не из нуля.
3) Ограниченность количественных значений ПУВ представляет собой конструктивно завершенный элемент.
Структурная схема ПУВ.
ЧЭ – чувствительный элемент. Основное требование: сигнал на выходе реагирует на малейшее изменение на входе. Характеристика: функция х*(х). х* может быть неэлектрической величиной.
ПФВ – преобразователь физической величины. Характеристика: функция z(x*), должна быть возрастающей.
МП – масштабный преобразователь. Уменьшает или увеличивает величину в заданное число раз. ФП – Функциональный преобразователь. Преобразует нелинейную величину в линейную. АЦП – аналогово-цифровой преобразователь. ГР – гальваническая развязка. Защищает преобразователь от помех.
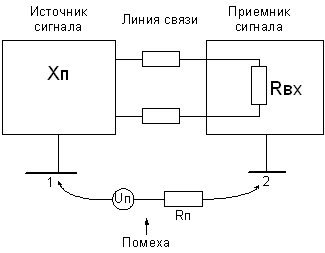
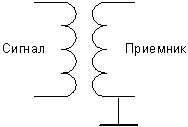
Между точками 1 и 2 может быть разность потенциалов. Если потенциалы точек разные то между ними пройдет помеха. Гальваническая развязка может быть реализована с помощью трансформатора.
Двоично-десятичная система. Двоично-десятичная система сохраняет надежность двоичной системы с наглядностью и меньшей избыточностью десятичной системы. Каждый разряд десятичного числа кодируется двоичным числом. Например, для кодирования чисел от 0 до 999 требуется 12 элементов с 2 устойчивыми состояниями.
Преобразователь аналогового сигнала в аналоговый (ПАА). ПАА разделяют на 2 группы:
Пассивные преобразователи.
Задача: на нагрузку подается ток ~5 ампер. Необходимо точно определить величину этого тока, имея в распоряжении миллиамперметр, предел измерения которого 100 мА.
Для этого амперметр шунтируется сопротивлением, которое определяется следующим образом:
Задача: необходимо получить напряжение на выходе в к раз меньше, чем на входе.
Примечания. 1. Коэффициент делителя может меняться в зависимости от нагрузки. Обозначим:
2. При работе на высоких частотах возникает ощутимая реактивная составляющая сопротивления.
3. Реальные делители, как правило, многоступенчатые.
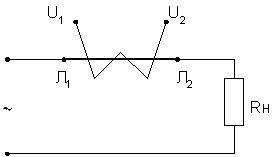
3. Измерительные трансформаторы тока и напряжения. Измерительные трансформаторы тока и напряжения предназначены для преобразования тока и напряжения на первичной обмотке в ток и напряжение на вторичной обмотке в заданное число раз с высокой точностью. Трансформатор тока.
Л1Л2 – первичная обмотка. U1U2 – измерительная обмотка.
Аварийный режим трансформатора тока: холостой ход измерительной обмотки.
Трансформатор напряжения. Холостой ход измерительной обмотки является рабочим режимом трансформатора напряжения.
Аварийным режимом трансформатора напряжения является короткое замыкание измерительной обмотки.
Коэффициент трансформации. Коэффициент трансформации трансформатора тока. Номинальный: Действительный: Коэффициент трансформации трансформатора напряжения. Номинальный: Действительный: Векторная диаграмма трансформатора тока и напряжения. ВД идеального трансформатора тока.
ВД реального трансформатора тока.
ВД идеального трансформатора напряжения.
ВД реального трансформатора напряжения.
Реально отклонение Векторная диаграмма трансформатора тока.
Аварийный режим: Очевидно:
Полные характеристики
1. Переходная характеристика
2. Импульсная характеристика
3. 3. АФХ АФХ – АЧХ и ФЧХ (характеризует запаздывание)
ПРИМЕР:
1. 2. 3. Пусть динамика описывается уравнением 1:
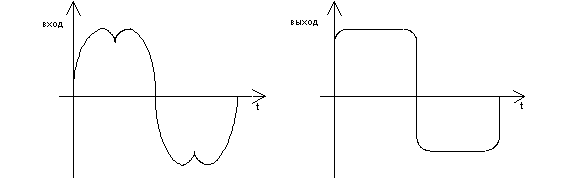
а) будет ли запаздывание б) будет ли искажение
ПРИМЕР 2: Что будет на выходе?
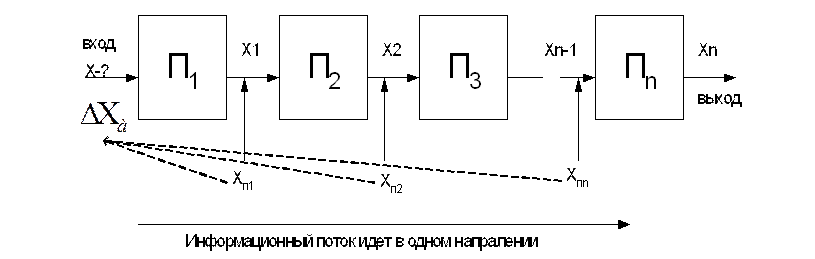
Структурные схемы измерения 1. прямого преобразования 2. компенсационного преобразования 2.1 с астатической характеристикой 2.2 со статической характеристикой 3. с автоматической коррекцией погрешности 1.Структурные схемы измерения прямого преобразования
Функции преобразования отдельных блоков могут быть линейными и нелинейными. Пусть все функции линейные:
Функции преобразования: Возникают погрешности: 1.
Идеальный случай: Хп=КХ при всех Реальный случай:
При последовательном включении блоков их число ограничено. Можно подобрать блоки с различным
2.
ПРИМЕР:
При наличие помехи, первый каскад нужно делать очень тщательно (экранирование, заземление, использование качественных кабелей). Фильтры не всегда помогают, так как они влияют на динамику.
2. Структурные схемы измерения компенсационного преобразования
2.1 Структурные схемы измерения компенсационного преобразования с астатической характеристикой
S=
Чтобы реализовать такой режим работы, в любом месте цепи прямого преобразования должно стоять запоминающее интегрирующее звено.
В связи с тем, что современные интегрирующие устройства обладают невысокой чувствительностью, то обычно их ставят в конце цепи. Возникают погрешности: 1.
Цепь отрицательной обратной связи выполняется на пассивных элементах
2. внутренние дрейфы порог чувствительности интегратора Будем считать, что помехи воздействуют на цепь прямого преобразования, так как цепь обратной связи низкоомная. Приведем помехи на вход:
Введение отрицательной обратной связи
2.2 Структурные схемы измерения компенсационного преобразования со статической характеристикой
bK-петлевое усиление.
Возникают погрешности: 1.
1. при больших Kb, 2. При больших Kb, замкнутая система может потерять устойчивость, т.е система будет реагировать не на сигнал, а на внутренние флуктуации
Компромисс между точностью и устойчивостью может быть найден при:
2.
Введение отрицательной обратной связи не уменьшает аддитивную погрешность.
Теория Погрешностей 1. причины появления погрешностей результата измерений 2. погрешности систематические и случайные, описание случайных погрешностей 3. идеи суммирования погрешностей 4. обработка ряда прямых наблюдений для получения результатов измерений
1. причины появления погрешностей результата измерений
схема измерения эксперимента
Результат нужен для того, чтобы иметь однозначную информацию об измеряемой величине. Погрешность результата измерений: Хр – истинное значение Хn – результат измерений
Причины: -погрешность метода ПРИМЕР: Объект измерений – генератор А) модель
V-вольтметр, измеряющий действующее значение
Б) реально:
если если не не учитывается, что сигнал отличается от синусоидального
- инструментальная погрешность (ею обладает средство измерения) - погрешность от влияния средства измерения на объект измерения. ПРИМЕР:
Есть 3 амперметра:
- погрешность человека-экпериментатора - погрешность, связанная с ЭВМ (погрешность округления)
2. погрешности систематические и случайные, описание случайных погрешностей Погрешность результата формируется под воздействием факторов: I. факторы, которые в процессе измерения остаются постоянными или меняются по закону, следовательно, формируются систематические погрешности II. факторы, которые в процессе измерения меняются случайным образом с интенсивностью, которую трудно предсказать, следовательно, формируются случайные погрешности
ПРИМЕР 1:
можно свести
ПРИМЕР 2:
ПРИМЕР 3:
Если
Как свести Методы: 1. правильная постановка эксперимента.
2. введение поправочных кривых, графиков и т.д 3. специальные методы ПРИМЕР:
Случайная величина полностью описывается законами распределения интегрирующими и дифференцирующими (плотностью распределения вероятности). На практике – дифференцирующими законами. ПРИМЕР:
Известен дифференцирующий закон распределения, следовательно, можно найти вероятность того факта, что измеряемая величина находится между Х1 и Х2.
Во многих случаях измеряемая величина распределяется около истинного значения Q (но не всегда). Плотность распределения погрешностей:
ПРИМЕР:
Как с помощью вероятностных характеристик оценить погрешность? Оценку погрешности производят с помощью доверительных интервалов и доверительной погрешности:
k- коэффициент, зависящий от р(х) и Рдов
3. идеи суммирования погрешностей
1. первый подход 2. второй подход: суммируются погрешности на основании вероятностных характеристик
1. если законы распределения не Гауссов, то при n>3 возникают сложности 2. может возникать трансформация закона суммарного распределения. ПРИМЕР:
На практике существует только 2 значения доверительной вероятности.
ПРИМЕР:
r-коэффициент корреляции (коэффициент связи)
r = 0 – некоррелированы
На практике:
ПРИМЕР:
Примечание: При суммирование погрешностей обычно аддитивные и мультипликативные составляющие суммируются отдельно друг от друга.
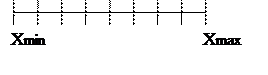
4. обработка ряда прямых наблюдений для получения результатов измерений Обработка результатов предполагает, что одну и ту же величину измеряют много раз в одинаковых условиях. Х - измеряемая величина n>40 – количество измерений Из ряд наблюдений нужно исключить промахи (по определенным методам). Ранжирование: Хmin … Xmax Ищем оценки числовых параметров: 1). оценка математического ожидания
2). оценка СКО:
3). найти закон распределения:
1. 2. из всех n находим частоту попадания на интервал 3.
3. По виду гистограммы выдвигается гипотеза, какому закону распределения она соответствует. 4. Критерий согласия: например, Для подсказки в измерительной технике говорится, какие законы распределения наиболее используются:
4).
Примечание: Существуют случаи, когда не нужно строить гистограмму для определенного закона распределения: - когда имеются статистиче
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.013 с.) |


 физическая величина.
физическая величина.


 .
. X = Xп = 3A
X = Xп = 3A

 - это число различимых градаций
- это число различимых градаций







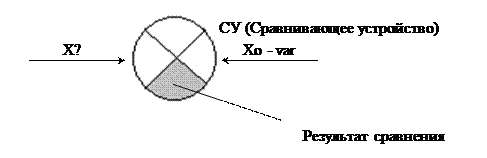




 еет мерить ЭДС.
еет мерить ЭДС. А).
А).




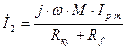
 (компенсатор частоты).
(компенсатор частоты).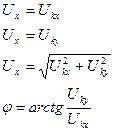


 или
или  .
.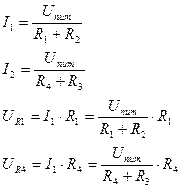




 Ом.
Ом.







 = 1 кОм (5%, 10%)
= 1 кОм (5%, 10%) = 1 кОм. Затем меняем сопротивление R2 пока не добьёмся Iни = 0 (нулевой метод). После этого в точки с и d вставляем новые резисторы и смотрим, равны ли номинальному
= 1 кОм. Затем меняем сопротивление R2 пока не добьёмся Iни = 0 (нулевой метод). После этого в точки с и d вставляем новые резисторы и смотрим, равны ли номинальному  . Если не равны, то отбраковываем (если
. Если не равны, то отбраковываем (если 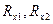 не равны номинальному, следовательно Iни ≠ 0).
не равны номинальному, следовательно Iни ≠ 0). . Записывают показания амперметра. Существует градуированный график, по которому возможно по значению тока узнать искомую температуру.
. Записывают показания амперметра. Существует градуированный график, по которому возможно по значению тока узнать искомую температуру.












 где
где  - сопротивление амперметра,
- сопротивление амперметра,  - сопротивление шунта,
- сопротивление шунта, 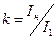 - коэффициент шунта.
- коэффициент шунта.



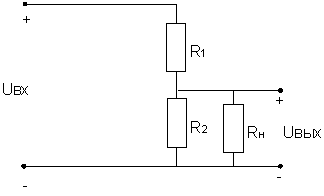
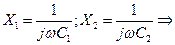


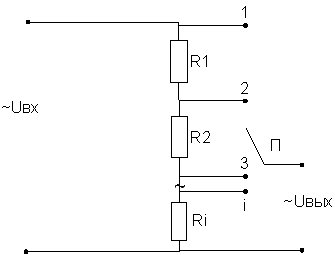








 составляет несколько минут.
составляет несколько минут.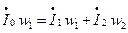 , где
, где 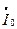 - намагничивающий ток,
- намагничивающий ток,  - ток первичной и вторичной обмотки соответственно,
- ток первичной и вторичной обмотки соответственно,  число витков первичной и вторичной обмотки соответственно.
число витков первичной и вторичной обмотки соответственно.  - потери на гистерезис и вихревые токи.
- потери на гистерезис и вихревые токи.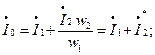


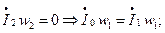



 при ННУ
при ННУ при ННУ
при ННУ

 резонанс
резонанс
 - возможно искажение
- возможно искажение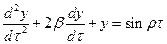
 - соотношение частот
- соотношение частот 
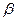 - степень успокоения
- степень успокоения
 зависит от
зависит от 

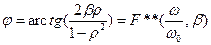
 т.0 =>
т.0 => 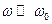

 Найти: Хп=F(x) – функция всего устройства в целом.
Найти: Хп=F(x) – функция всего устройства в целом.
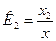 …
… 
 , где
, где  (1)
(1)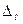 ←
←  ←
← 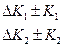 ←влияние внешних факторах
←влияние внешних факторах 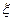

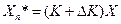 при всех
при всех 

 ←внешние помехи и внутренние дрейфы←Хп
←внешние помехи и внутренние дрейфы←Хп
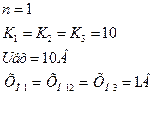


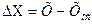
 =0
=0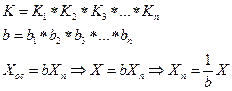 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент преобразования всего устройства
- коэффициент преобразования всего устройства
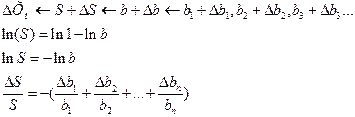
 ее можно сделать более стабильной
ее можно сделать более стабильной  .
.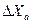 ←внешние помехи
←внешние помехи

 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент S зависит только от b и K.
- коэффициент S зависит только от b и K.
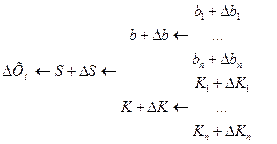



 , т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи
, т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи 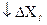 .
.

 вешние помехи, внутренние дрейфы→Хп
вешние помехи, внутренние дрейфы→Хп



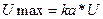
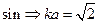


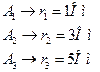
 , т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно.
, т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно. - истинное
- истинное

 , где
, где 
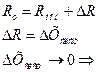
 к минимуму
к минимуму Делая многократные измерения одной и той же величины, можно получить (выявить)
Делая многократные измерения одной и той же величины, можно получить (выявить) 

 , тогда
, тогда  рассчитывается методами теории вероятности.
рассчитывается методами теории вероятности.




 На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
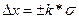
 - доверительный интервал
- доверительный интервал применяются такие значения в измерительной технике
применяются такие значения в измерительной технике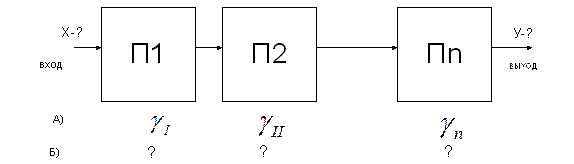



 при Рдов = …
при Рдов = … - суммарное СКО
- суммарное СКО
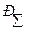 - суммарный закон распределения
- суммарный закон распределения
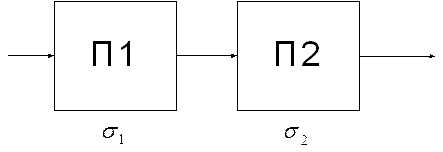

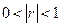
 - коррелированы (
- коррелированы ( )
)


 - ряд наблюдений
- ряд наблюдений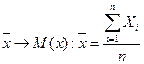

 гистограмма
гистограмма делится на нечетное число
делится на нечетное число






 - гарантия разброса относительно среднего с определенной вероятностью
- гарантия разброса относительно среднего с определенной вероятностью


