
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные динамические характеристикиСодержание книги Поиск на нашем сайте 1. собственная частота 2. коэффициент успокоения 3. время установления показаний – промежуток времени от момента изменения измеряемой величины до того момента, когда показания не будут выходить за определенную зону.
Обычно электромеханические приборы имеют время установления показаний меньше, чем 4 с, а цифровые приборы делают Если есть дифференциальное уравнение, то время установления показаний равно бесконечности.
Взаимосвязь мощности, быстродействия и точности с точки зрения информационно-энергетической теории измерительных устройств
Рассматривается процесс передачи информации, как энергетический процесс.
Для того, чтобы получить на выходе информацию, нужно затратить энергию. Wпол появляется из-за того, что мы от объекта измерений отбираем W=Pt. Чем больше нужно получить Wпол, тем больше нужно будет забрать W=Pt. Количество информации, получаемой при измерении, в зависимости от потребляемой мощности подчиняется второму закону термодинамики и может быть реализовано с КПД не более, чем у тепловых машин.
Отношение полезной энергии к затраченной много меньше единицы → пропадает часть энергии → пропадает часть информации в средстве измерения (так как средство измерения имеет погрешность). Если средство измерения идеально (гипотетически), то точность измерений принципиально ограничена: 1. дискретностью измеряемой величины 2. флуктуациями, связанными с принципиальной дискретностью вещества и энергии Средство измерения состоит из элементов, имеющих шумы (флуктуаций): 1. магнитный 2. тепловой 3. дробовой Следовательно, есть энергия шума Wш Условия осуществления измерений: Но при этом точность ограничена. С – энергетический порог чувствительности: Тепловой шум: Средняя мощность
тепловую мощность и тепловую энергию можно рассчитать при Т-var при
1. для одновременного улучшения все 3 характеристики нужно ↑ 2. если 3. можно определить будет ли выполнить здание или нет (возможно ли создание всех условий)
Нормирование метрологических характеристик Норма – результат соглашения между потребителем и изготовителем. Нормирование –регламентация того факта, каким должен быть прибор.
Что нормируется? - Все характеристики, влияющие на точность полученного результата измерения 1. характеристики, с помощью которых определяется результат измерений - функции преобразования - шкала деления - количество разрядов кода - единица последнего разряда кода 2. чувствительность влияющих факторов 3. погрешности 4. характеристики связи средства измерения с объектом и нагрузкой 5. динамические характеристики 6. неинформативные параметры
ПРИМЕР: Сигнал Ели Ели Ели
Нормирование погрешностей: I. нормируются вероятностные характеристики погрешности II. нормируются предельные значения погрешностей:
Нормирование предельного значения погрешности: 1. - -
2. - - 3. -
Для измерительных приборов вводится понятие класс точности – величина, численно равная максимальному значению К - класс точности. 1.
3. приборы, у которых нормируется  : :
Пример:
Структурные схемы измерения 1. прямого преобразования 2. компенсационного преобразования 2.1 с астатической характеристикой 2.2 со статической характеристикой 3. с автоматической коррекцией погрешности 1.Структурные схемы измерения прямого преобразования
Функции преобразования отдельных блоков могут быть линейными и нелинейными. Пусть все функции линейные:
Функции преобразования: Возникают погрешности: 1.
Идеальный случай: Хп=КХ при всех Реальный случай:
При последовательном включении блоков их число ограничено. Можно подобрать блоки с различным
2.
ПРИМЕР:
При наличие помехи, первый каскад нужно делать очень тщательно (экранирование, заземление, использование качественных кабелей). Фильтры не всегда помогают, так как они влияют на динамику.
2. Структурные схемы измерения компенсационного преобразования
2.1 Структурные схемы измерения компенсационного преобразования с астатической характеристикой
S=
Чтобы реализовать такой режим работы, в любом месте цепи прямого преобразования должно стоять запоминающее интегрирующее звено.
В связи с тем, что современные интегрирующие устройства обладают невысокой чувствительностью, то обычно их ставят в конце цепи. Возникают погрешности: 1.
Цепь отрицательной обратной связи выполняется на пассивных элементах
2. внутренние дрейфы порог чувствительности интегратора Будем считать, что помехи воздействуют на цепь прямого преобразования, так как цепь обратной связи низкоомная. Приведем помехи на вход:
Введение отрицательной обратной связи
2.2 Структурные схемы измерения компенсационного преобразования со статической характеристикой
bK-петлевое усиление.
Возникают погрешности: 1.
1. при больших Kb, 2. При больших Kb, замкнутая система может потерять устойчивость, т.е система будет реагировать не на сигнал, а на внутренние флуктуации
Компромисс между точностью и устойчивостью может быть найден при:
2.
Введение отрицательной обратной связи не уменьшает аддитивную погрешность.
Теория Погрешностей 1. причины появления погрешностей результата измерений 2. погрешности систематические и случайные, описание случайных погрешностей 3. идеи суммирования погрешностей 4. обработка ряда прямых наблюдений для получения результатов измерений
1. причины появления погрешностей результата измерений
схема измерения эксперимента
Результат нужен для того, чтобы иметь однозначную информацию об измеряемой величине. Погрешность результата измерений: Хр – истинное значение Хn – результат измерений
Причины: -погрешность метода ПРИМЕР: Объект измерений – генератор А) модель
V-вольтметр, измеряющий действующее значение
Б) реально:
если если не не учитывается, что сигнал отличается от синусоидального
- инструментальная погрешность (ею обладает средство измерения) - погрешность от влияния средства измерения на объект измерения. ПРИМЕР:
Есть 3 амперметра:
- погрешность человека-экпериментатора - погрешность, связанная с ЭВМ (погрешность округления)
2. погрешности систематические и случайные, описание случайных погрешностей Погрешность результата формируется под воздействием факторов: I. факторы, которые в процессе измерения остаются постоянными или меняются по закону, следовательно, формируются систематические погрешности II. факторы, которые в процессе измерения меняются случайным образом с интенсивностью, которую трудно предсказать, следовательно, формируются случайные погрешности
ПРИМЕР 1:
можно свести
ПРИМЕР 2:
ПРИМЕР 3:
Если
Как свести Методы: 1. правильная постановка эксперимента.
2. введение поправочных кривых, графиков и т.д 3. специальные методы ПРИМЕР:
Случайная величина полностью описывается законами распределения интегрирующими и дифференцирующими (плотностью распределения вероятности). На практике – дифференцирующими законами. ПРИМЕР:
Известен дифференцирующий закон распределения, следовательно, можно найти вероятность того факта, что измеряемая величина находится между Х1 и Х2.
Во многих случаях измеряемая величина распределяется около истинного значения Q (но не всегда). Плотность распределения погрешностей:
ПРИМЕР:
Как с помощью вероятностных характеристик оценить погрешность? Оценку погрешности производят с помощью доверительных интервалов и доверительной погрешности:
k- коэффициент, зависящий от р(х) и Рдов
3. идеи суммирования погрешностей
1. первый подход 2. второй подход: суммируются погрешности на основании вероятностных характеристик
1. если законы распределения не Гауссов, то при n>3 возникают сложности 2. может возникать трансформация закона суммарного распределения. ПРИМЕР:
На практике существует только 2 значения доверительной вероятности.
ПРИМЕР:
r-коэффициент корреляции (коэффициент связи)
r = 0 – некоррелированы
На практике:
ПРИМЕР:
Примечание: При суммирование погрешностей обычно аддитивные и мультипликативные составляющие суммируются отдельно друг от друга.
4. обработка ряда прямых наблюдений для получения результатов измерений Обработка результатов предполагает, что одну и ту же величину измеряют много раз в одинаковых условиях. Х - измеряемая величина n>40 – количество измерений Из ряд наблюдений нужно исключить промахи (по определенным методам). Ранжирование: Хmin … Xmax Ищем оценки числовых параметров: 1). оценка математического ожидания
2). оценка СКО:
3). найти закон распределения:
1. 2. из всех n находим частоту попадания на интервал 3.
3. По виду гистограммы выдвигается гипотеза, какому закону распределения она соответствует. 4. Критерий согласия: например, Для подсказки в измерительной технике говорится, какие законы распределения наиболее используются:
4).
Примечание: Существуют случаи, когда не нужно строить гистограмму для определенного закона распределения: - когда имеются статистические данные - когда закон распределения уже известен - если результат измерений формируется под действием большого числа независимых факторов, причем вклад каждого фактора в результат одинаков, то можно считать, что закон нормальный (N>5). - Если закон распределения нормальный, а n>10, то можно пользоваться распределением Стьюдента:
ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ 1. структурная схема электромеханических приборов (с элементами классификации) 2. моменты, действующие в приборах 3. магнитоэлектрические измерительные приборы 4. магнитоэлектрический амперметр и вольтметр 5. магнитоэлектрический омметр 6. магнитоэлектрический гальванометр 7. баллистический гальванометр (применение для измерения магнитного потока) 8. электродинамические измерительные механизмы 9. электродинамический амперметр и вольтметр 10. электродинамический ваттметр 11. индукционный измерительный механизм 12. индукционный счетчик энергии 1. структурная схема электромеханических приборов (с элементами классификации)
Риц, Рим, Роу – параметры ИЦ, ИМ, ОУ
коррекции (обычно в ИЦ) 2. моменты, действующие в приборах 1) вращательный момент магнит возникает и тянет подвижную часть слева направо.
Так как подвижная часть обладает большой массой, то реагирует не на мгновенное значение, а на среднее.
2) противодействующий момент Мпр (искусственный) Мпр действует слева направо. Его можно создать механическим или электрическим путем.
Существует устойчивое положение равновесия, когда:
ПРИМЕР:
Получаются однозначные показания, т.е. каждому значению измеряемой величины соответствует одно показание.
Муст=Мвр-Мпр устанавливающий момент, который возникает сам, если:
Если прибор находится в состоянии равновесия, а его выводят из этого состояния, то появляется Муст.
3) Момент успокоения, возникающий в динамике
3. магнитоэлектрические измерительные приборы
1) с механическим противодействующим моментом прибор с подвижной рамкой:
ПН – полюсные наконечники. С - сердечник. ПР – подвижная рамка.
Через рамку пропускается переменный или постоянный ток на низкой частоте. Рамка находится в магнитном поле индукции В. Форма ПН и С сделана так, что в зазоре обеспечивается радиальное, равномерное, постоянное поле индукции В. ПН и С – из магнитномягкого материала. N и S - из магнитотвердого материала.
Особенности: 1. 2. прибор полярный
2) Логометр
Поверхности не цилиндрические.
Прибор для измерения соотношения токов.
IV 1. Систематические погрешности Δс 2. Случайные погрешности Δслуч Δс – это погрешность, которая меняется по определенному закону или или остается постоянной при многократном измерении одной и той же величины; Δс стараются свести к 0. Δслуч – это погрешность, возникающая и исчезающая с интенсивностью, которую трудно предсказать, при многократном изменении одной и той же величины. Δ= Δс+ Δслуч 5. импеданс
диапазон измерений – это диапазон тех значений, которые могут быть измерены с определеной точностью. Пример:
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


 измерений в секунду.
измерений в секунду.




 - погрешность
- погрешность
 - постоянна Больцмана
- постоянна Больцмана - полоса частот
- полоса частот - температура, К
- температура, К


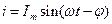
 -информативный параметр, то
-информативный параметр, то  - неинформативные параметры.
- неинформативные параметры. -информативный параметр, то
-информативный параметр, то 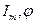 - неинформативные параметры.
- неинформативные параметры. -информативный параметр, то
-информативный параметр, то  - неинформативные параметры.
- неинформативные параметры.
 :
: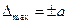

 :
:
 , где
, где  - конечное значение шкалы, х- текущее значение шкалы
- конечное значение шкалы, х- текущее значение шкалы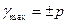
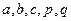 - числовые значения
- числовые значения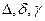 , а так же учитывающая характеристики, влияющие на точность измерений.
, а так же учитывающая характеристики, влияющие на точность измерений. приборы, у которых нормируется
приборы, у которых нормируется  2. приборы, у которых нормируется
2. приборы, у которых нормируется 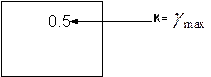

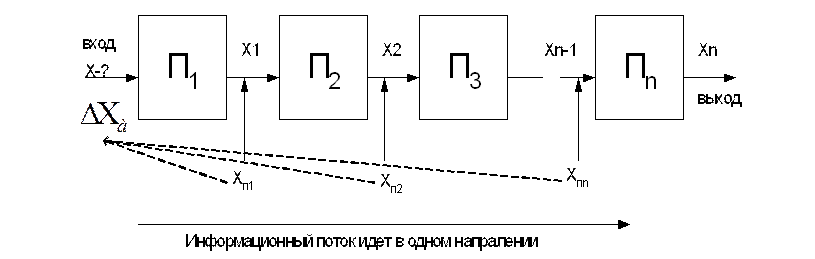 Найти: Хп=F(x) – функция всего устройства в целом.
Найти: Хп=F(x) – функция всего устройства в целом.
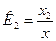 …
… 
 , где
, где  (1)
(1)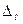 ←
←  ←
← 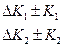 ←влияние внешних факторах
←влияние внешних факторах 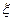

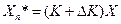 при всех
при всех 

 ←внешние помехи и внутренние дрейфы←Хп
←внешние помехи и внутренние дрейфы←Хп
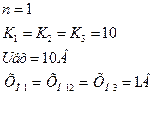


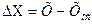
 =0
=0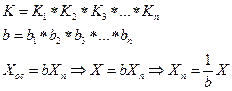 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент преобразования всего устройства
- коэффициент преобразования всего устройства
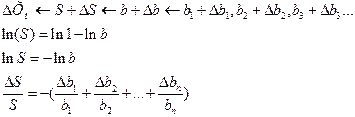
 .
.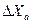 ←внешние помехи
←внешние помехи

 - функция преобразования всего устройства
- функция преобразования всего устройства - коэффициент S зависит только от b и K.
- коэффициент S зависит только от b и K.
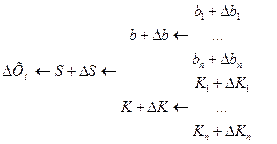



 , т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи
, т.е нестабильность всего устройства определяется нестабильностью цепи обратной связи 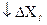 .
.

 вешние помехи, внутренние дрейфы→Хп
вешние помехи, внутренние дрейфы→Хп



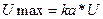
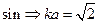


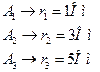
 , т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно.
, т.е если сопротивление амперметра разное, то и ток будет азным, но разность токов эксперимент произведен неверно. - истинное
- истинное

 , где
, где 
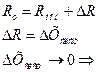
 к минимуму
к минимуму Делая многократные измерения одной и той же величины, можно получить (выявить)
Делая многократные измерения одной и той же величины, можно получить (выявить) 

 , тогда
, тогда  рассчитывается методами теории вероятности.
рассчитывается методами теории вероятности.




 На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
На практике вместо законов распределения пользуются их оценками числовых параметров (оценки моментов) или числовыми параметрами (моменты)
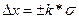
 - доверительный интервал
- доверительный интервал применяются такие значения в измерительной технике
применяются такие значения в измерительной технике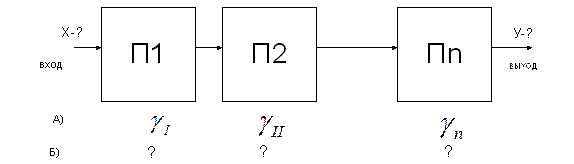



 при Рдов = …
при Рдов = … - суммарное СКО
- суммарное СКО
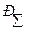 - суммарный закон распределения
- суммарный закон распределения
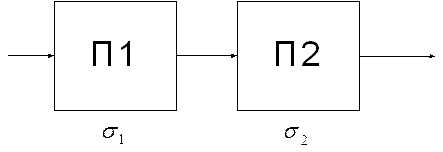

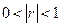
 - коррелированы (
- коррелированы ( )
)


 - ряд наблюдений
- ряд наблюдений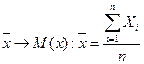

 гистограмма
гистограмма делится на нечетное число
делится на нечетное число






 - гарантия разброса относительно среднего с определенной вероятностью
- гарантия разброса относительно среднего с определенной вероятностью


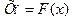 -однозначная функция
-однозначная функция нужно либо стабилизировать параметры, либо ввести схемы
нужно либо стабилизировать параметры, либо ввести схемы




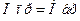





 N,S – постоянные магниты.
N,S – постоянные магниты. - угол поворота.
- угол поворота.
 -чувствительность по току
-чувствительность по току


 6. Диапазон измерений и диапазон показаний
6. Диапазон измерений и диапазон показаний



