Устойчивость динамических систем

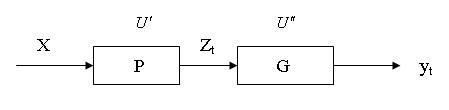
Пусть множество входных воздействий содержат элементы в интервале (-∞; +∞) и пусть p = [p_k, k={1,k}] семейство операторов перехода, которые при заданном множестве входных воздействий X^ реализуют полное множество Z^ состояний системы мощностно Z^ = M₁ ⋅ M₂ ⋅... ⋅ M_N

Реальный объект имеет вполне определенный оператор переходов p_k ⊂ p и находится под воздействием определенного множества входных сигналов X ⊂ X^. Если для заданных Х и p_k существует соотношение

Z_t = p_k{(t₀, t), Z_t0, X},

то множество [Z_t0, Z_t1,..., Z_t] на любом интервале наблюдения является замкнутым, а система

S = [p_k, G, X, Y, T]

устойчивой относительно множества входных воздействий Х.

Управляемость динамических систем

В общем случае задача управления формируется в следующем виде. Известно множество входных сигналов Х, и семейство операторов перехода Р и выходов G. Задано необходимое значение выхода Y_t в момент времени t. Найти управляющее воздействие v ∈ V обеспечивающие выбор операторов перехода p ∈ P и выхода g ∈ G обеспечивающие необходимое y_t.

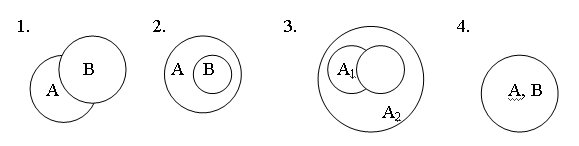
Исходя из общей формулировки задачи управления, необходимо различать управление множеством выходов. Достижение цели управления обеспечивается выбором операторов p и q.

Система является управляемой, если для заданных X_t ⊂ X и C_t ⊂ C, существуют такие C_t0 ⊂ C, что существуют p(C,X_t) ⊂ P или g(C_t,y_t).

Отсюда следует, что управление может осуществляться начальным состоянием, операторами переходов и выходов. При этом задача управления сводится к следующему. Известно x ⊂ X, p ⊂ P, g ⊂ G. Задано y_t = y ⊂ Y. Необходимо найти v ⊂ V при котором p(c_t = c ⊂ C, x_t = x ⊂ X) и g(y_t = y ⊂ Y, c_t = c ⊂ C).

Интегративные свойства систем

В предыдущих разделах были рассмотрены структурные и динамические свойства систем, которые не связаны с какой либо физической природой объекта анализа и вытекают из математических свойств абстрактных множеств.

Интегративные свойства систем охватывают структурные и динамические свойства одновременно, носят прикладной характер и базируются на принципах и закономерностях естествознания. Они проявляются на множестве отношений свойств объекта и внешней среды. Т.е. отражают результат их взаимодействий в виде изменений объекта и внешней среды.

Характер взаимодействия объекта и внешней среды может быть различным: сплоченным или разобщенным. При этом соответственно и результаты взаимодействия могут быть положительными и отрицательными. В этом смысле рассмотрим две группы наиболее общих интегративных свойств, связанных с оценкой возможности возникновения положительных результатов (качество и эффективность) и отрицательных результатов (безопасность и живучесть).

Качество системы

Качество системы представляет виртуальную оценку возможности получения положительного результата взаимодействия объекта с внешней средой.

Под качеством понимается обобщенная положительная характеристика системы, которая показывает ее полезность для макросистемы, состоящей из двух подсистем: объекта и внешней среды.

Для выражения качество служит показателем качества — положительное свойство системы. Суждение о качестве системы основывается на сравнении показателя качества одной системы с показателем качества другой системы реально существующей или виртуальной. Решение о качестве принимается на основе критерия — правило выбора альтернатив (вариантов).

Рассмотрим следующую задачу. Пусть А — множество свойств виртуальной системы, т. е. потребностей макросистемы. В — множество свойств системы. Здесь возникают несколько вариантов, представленные на рисунках.

Рис. — Соотношение множеств свойств систем А и A₁ и потребностей макросистемы В.

1. Система не удовлетворяет потребностям макросистемы и следовательно непригодна.

2. Система удовлетворяет потребностям по возможности по использование ее ресурса нерационально |А| > |B|.

3. Система A₂ удовлетворяет потребностям макросистемы, поэтому она превосходит систему A₁.

4. Система пригодна и рационально расходует свой ресурс.

Из рассмотренных примеров вытекают три основных критерия качества системы пригодности, превосходства и оптимальности.

Эффективность

Понятие эффективность связано с целенаправленными процессами, т. е. процессом функционирования некоторой системы, которая организуется и проводится для достижения определенной цели, т. е. получение определенного результата.

Характеризуя целенаправленный процесс необходимо различать качества определенных получаемых результатов и качество множества результатов рассматриваемых как единое целое. Последнее характеризует уровень достижения цели. Это свойство будет называться эффективностью целенаправленного процесса (операции).

Свойство обобщенного результата операции условно можно разделить на три группы:

• результативность (целевой эффект)
• ресурсоемкость
• оперативность (расход времени)

Соответственно показатели эффективности отражают одну из групп свойств или совместно все. В этой связи эффективностью называют комплексное свойство целенаправленного процесса.

Показатели эффективности

Показатели эффективности должны удовлетворять ряду общих обязательных требований. Основными из них являются: представительность, полнота, стохастичность, простота.

Представительность означает, что эффективность должна оцениваться относительно главной цели операции, а показатель должен иметь прямое отображение цели, характеристик процесса и внешней среды.

Количественная величина показателя должна быть чувствительна к изменению характеристик процесса и случайных факторов во внешней среде. А математическая модель должна обеспечивать проведение необходимых измерений и вычислений в приемлемые сроки.

В общем виде показатель эффективности имеет вид вектора

α = <R_ц, R_р, T>

где R_ц — целевые эффекты,

R_р — ресурсоемкость, Т — затраты времени.

Поскольку процесс функционирования системы протекает во внешней среде с характеристиками V, состав этих характеристик оказывает влияние на R_ц, R_р и Т то реально величина Э представляет множество

Э(V) = [e(u_n), n={1,N}]

Поэтому цель операции формально можно представить в следующем виде.

Э(V) ⊂ {Э_дон.}.