
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Люминесценция. Спектры люминесценции. Виды люминесценции. Закон Стокса для фотолюминесценции. Хемилюминесценция. Люминесцентная микроскопия.Содержание книги
Поиск на нашем сайте
Люминесценция. Спектры люминесценции. Виды люминесценции. Закон Стокса для фотолюминесценции. Хемилюминесценция. Люминесцентная микроскопия. Люминесценцией называют избыточное над тепловым излучение тела, имеющее длительность, значительно превышающую период (~10-15с) излучаемых световых волн. Первая часть определения отделяет люминесценцию от равновесного теплового излучения. Люминесценция обычно наблюдается в видимой или ультрафиолетовых областях спектра. Тепловое излучение в этой области возникает только при температуре в несколько сотен или тысяч градусов, тогда как люминесценция наблюдается при любых температурах, поэтому люминесценцию часто называют холодным свечение. Признак длительности в этом определении был предложен С. И. Вавиловым для того, чтобы отличить люминесценцию от некоторых других явлений вторичного свечения, например отражения или рассеяния света. Люминесцируют электронно-возбужденные молекулы (атомы). В зависимости от способа возбуждения различают несколько типов люминесценции. Люминесценция, вызванная заряженными частицами: ионами – ионолюминесценция, электронами – катодолюминесценция, ядерным излучением – радиолюминесценция. Люминесценцию под воздействием рентгеновского и Y(гамма)-излучения называют рентгенолюминесценцией, фотонов видимого света – фотолюминесценция. При растирании, раздавливании или раскалывании некоторых кристаллов возникает триболюминесценция. Электрическим полем возбуждается электролюминесценция, частным случаем которой является свечение газового разряда. Люминесценцию, сопровождающую экзотермическую химическую реакцию, называют хемилюминесценцией. Спектры Люминесценции Спектром люминесценции называют зависимость интенсивности люминесцентного излучения от длины волны испускаемого света. Наиболее простые — атомные спектры, в которых указанная выше зависимость определяется только электронным строением атома. Спектры молекул гораздо более сложные вследствие того, что в молекуле реализуются различные деформационные и валентные колебания. При охлаждении до сверхнизких температур сплошные спектры люминесценции органических соединений, растворенных в определенном растворителе, превращаются в квазилинейчатые. Это явление получило название эффекта Шпольского. Это ведёт к снижению предела обнаружения и повышению избирательности определений, расширению числа элементов, которые можно определять люминесцентным методом анализа. Фотолюминесценцией называется излучение электромагнитной энергии, возбуждаемое в веществе под действием оптического излучения ультрафиолетового или видимого диапазонов, избыточное по сравнению с тепловым излучением, при условии, что такое избыточное излучение имеет длительность, превышающую период электромагнитных колебаний (люминесценция) и время релаксационных процессов. Если облучить вещество (люминофор) в любом агрегатном состоянии ультрафиолетовым или видимым электромагнитным излучением, то возможно появление задержанного не менее, чем на 10-12 - 10-10 с, люминесцентного излучения. Максимум спектра этого излучения сдвинут относительно максимума спектра возбуждающего излучения в сторону меньших частот (закон Стокса - Ломмеля). Хемилюминесценция — люминесценция (свечение) тел, вызванная химическим воздействием или при протекании химической реакции.Хемилюминесценция связана с экзотермическими химическими процессами. Хемилюминесценция применяется для оценки состава сложных газовых смесей, в частности, наличия примесей в атмосфере. Достоинством этого метода является легкость автоматизации измерения и высокая селективность. Недостаток — ограниченный перечень анализируемых веществ. Люминесцентная микроскопия – метод микроскопии, позволяющий наблюдать первичную или вторичную люминесценцию микроорганизмов, клеток, тканей или отдельных структур, входящих в их состав. Цвет люминесценции, т.е. длина волны излучаемого света зависит от химической структуры и от физико–химического состояния микроскопируемого объекта, что и обусловливает возможность использования л.м. в целях микробиологической и цитологической диагностики, для дифференцирования отдельных компонентов клеток. Люминесцентный микроскоп снабжен мощным источником освещения с большой поверхностной яркостью, максимум излучения которого находится в коротковолновой области видимого спектра, системой светофильтров, а также интерференционной светоделительной пластинкой, применяемой при возбуждении люминесценции падающим светом. Источниками освещения для люминесцентного микроскопа чаще являются ртутно-кварцевые лампы сверхвысокого давления, а также лампы накаливания: ксеноновые и кварцево-галогенные. Для возбуждения люминесценции при люминесцентной микроскопии обычно используют длинноволновую ультрафиолетовую, сине-фиолетовую, а иногда и зелёную область спектра, в люминесцентном микроскопе применяют обычно стеклянную оптику и обычные предметные и покровные стёкла, пропускающие излучение в этой части спектра и не обладающие собственной люминесценцией. Иммерсионные и заключающие среды также должны соответствовать этим требованиям. Основными преимуществами Люминесцентной микроскопии являются высокая чувствительность (чувствительнее обычных цито- и гистохим. методов не менее чем в 1000 раз), легкость количественного измерения содержания различных хим. компонентов ткани и клеток, доступность аппаратуры. Для Л. м. органов и тканей используют первичную и вторичную люминесценцию. Спектрофотометрия. Спектрофлуориметрия. Спектрофотометрия — физико-химический метод исследования растворов и твёрдых веществ, основанный на изучении спектров поглощения в ультрафиолетовой (200—400 нм), видимой (400—760 нм) и инфракрасной (>760 нм) областях спектра. Основная зависимость, изучаемая в спектрофотометрии зависимость интенсивности поглощения падающего света от длины волны. Спектрофотометрия применяется при изучении строения и состава различных соединений, для качественного и количественного определения веществ (определения следов элементов в металлах, сплавах, технических объектах). Приборы спектрофотометрии — спектрофотометры. Спектрофлуориметрия. Принцип - испускание света, длина волны которого больше чем длина волны поглощенного света.. Применение - количественный анализ, кинетика, качественный анализ. Лазер. Распределение Больцмана. Понятия инверсной заселённости, вынужденного излучения. Рабочее вещество лазера. Виды источников энергетической накачки. Основные компоненты конструкции лазера. Особенности лазерного излучения. Лазер – квантовый генератор видимого диапазона излучения. Виды рабочего вещества лазера: газовые, жидкостные, полупроводниковые и твердотельные. Виды источников энергетической накачки: возбуждение очень интенсивным светом – «оптическая накачка», электрическим газовым разрядом, в полупроводниковых лазерах – электрическим током. Распределение Больцмана Распределение частиц по потенциальным энергиям в силовых полях – гравитационном, электрическом и др. – называют распределение Больцмана. Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации n молекул от высоты h над уровнем Земли или от потенциальной энергии молекулы m0gh:
Это выражение справедливо для частиц идеального газа.
Основными компонентами конструкции лазерной установки являются активная среда лазера, лазерная энергия накачки, высокий отражатель, прибор сцепки и лазерный луч. Активная среда лазера расположена в рефлексивной оптической впадине, куда направляется энергия накачки. Активная среда лазера – это материал, обладающий определенными свойствами, которые позволяют усиливать свет стимулируемой эмиссией. В своей самой простой форме эта впадина активной среды состоит из двух зеркал (одно из которых прозрачно), расположенных таким образом, что свет прыгает назад-вперед, каждый раз проходя через активную среду. Свет, проходя через активную среду, неоднократно усиливается, выходя пучком лучей со стороны прозрачного зеркала. Энергия накачки лазера, как правило, поставляется как электрический ток или как свет волнами различной длины. Такой свет может быть обеспечен лампой или другим лазером. Большинство практических лазеров содержит дополнительные элементы, которые отвечают за такие свойства, как длина волны излучаемого света или форма луча. Лазерное излучение уникально благодаря трем только ему присущим свойствам. 1) Когерентность. В физике существует 2 типа когерентности - пространственная и временная. Пространственная когерентность выражается в однотипности волнового фронта, т. е. пики и спады волн располагаются параллельно, когда свет выходит из лазера. Это обеспечивает синхронизацию фаз и фокусировку на очень маленькие участки. 2) Монохромность (временная когерентность). Это означает, что световые волны имеют одинаковую длину. Некоторые лазеры испускают лучи разной длины волны. Но явление это предсказуемо, и лазеры излучают свет только той длины, которая предусмотрена используемой в лазере средой. 3) Коллимация. Это означает, что все лучи, испускаемые лазером, параллельны и не рассеиваются с расстоянием. 51. Виды радиоактивных излучений. Радиоактивность. Закон радиоактивного распада. Радиоактивность-явление самопроизвольного превращения одних атомных ядер в другие, сопровождающееся испусканием различных видов ионизирующих излучений. Основные типы радиоактивного распада: А льфа-распад состоит в самопроизвольном превращении одно ядра в другое с испусканием α-частиц.
Пример альфа-распада для изотопа 238U
Бета-распад заключается во внеядерном взаимном превращении нейтрона и протона.
52.Ионизирующим излучением называется любое излучение, взаимодействие которого с веществом приводит к образованию ионов разных знаков. Взаимодействие с веществом α– излучения α-частицы сильно взаимодействуют с различными веществами, т. е. легко поглощаются ими. Тонкий лист бумаги или слой воздуха толщиной несколько сантиметров достаточны для того, чтобы полностью поглотить α-частицы. При прохождении через вещество a-частицы почти полностью отдают свою энергию в результате электростатического взаимодействия с электронами оболочек атомов. Энергия α-частиц идет на ионизацию и возбуждение атомов поглощающей среды (ионизационные потери). Этот процесс может рассматриваться как упругое столкновение α-частицы с электронами, при котором a-частица теряет часть своей энергии. Взаимодействие с веществом β- излучения β-частицы - это электроны (или позитроны), испускаемые ядрами радонуклидов при β-распаде. Вероятность взаимодействия β-частиц с веществом меньше, чем для α-частиц, так как β-частицы имеют в два раза меньший заряд и приблизительно в 7300 раз меньшую массу. Взаимодействие электронов и позитронов с веществом качественно одинаково и складывается из трех основных процессов: упругого рассеяния на атомных ядрах; рассеяния на орбитальных электронах; неупругих столкновений с атомным ядром. В случае применения тяжелых материалов возникает тормозное (вторичное) излучение, которое является рентгеновским и обладает большой проникающей способностью. Статистика. 1.Случайное событие – это событие, которое при данных условиях может произойти, либо не произойти. Относительная частота событий называется вероятностью и показывает отношение числа ожидаемых событий к числу возможных. Статистическое определение вероятности подразумевает под собой вероятность как предел, к которому стремится относительная частота. При классическом определении отн. частота и вероятность совпадают. В этом случае должно быть известно должны быть известны полное число возможных событий и число ожидаемых событий (орёл-решка, кубики и тп). Совместные события могут происходить параллельно друг другу; несовместные события исключают появление друг друга в ходе проводимого опыта. Зависимым называется событие, на вероятность которого оказывает влияние исход какого-либо иного события. Независимые наоборот. 2.Теорема сложение вероятностей: вероятность появление какого-либо события из нескольких несовместных равна сумме их вероятностей (или то, или другое) Теорема умножения вероятностей: Вероятность совместного появления независимых событий равна произведению их вероятностей(и то и другое). Условная вероятность — вероятность одного события при условии, что другое событие уже произошло(опыт с шариками в мешке, которые вытаскивают и не возвращают) 3. Дискретные. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины(возможные значения которой образуют конечную или бесконечную последовательность чисел). Закон распределения может быть задан аналитически, в виде таблицы или графически. Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин. Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим. 4. Непрерывные случайные величины всегда имеют вероятность равную нулю, поскольку количество её возможных численных значений бесконечно велико. Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин. Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим. 5. Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Примеры: 1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1
Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1. 2) дискретная биномиальная случайная величина (биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом:
где Число успехов в n испытаниях схемы Бернулли имеет биномиальное распределение. 3) дискретная случайная величина Пуассона(пуассоновское распределение с параметром). Закон распределения дискретной случайной величины Пуассона задается следующим образом:
Закон распределения случайной величины Пуассона носит название закона редких событий, например, число вызовов, поступивших на телефонную станцию, число распавшихся нестабильных частиц и т.д. 4) дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид
Пусть производятся независимые испытания, причем в каждом испытании возможны два исхода - "успех" с вероятностью p или "неуспех" с вероятностью 1 - p, 0 < p < 1. Обозначим через число испытаний до первого появления "успеха", тогда будет дискретной геометрической случайной величиной. Распределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого
Примеры 1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение).Важная роль этого распределения объясняется тем, что оно обычно возникает в явлениях, подверженных действию большого числа малых случайных величин. Так, математическая теория выборочного метода в статистике для расчета некоторых показателей широко использует нормальное распределение. 2)экспоненциальная (показательная) непрерывная случайная величина(экспоненциальное распределение).Экспоненциальному распределению подчиняется время распада ядер атомов различных элементов. Оно обладает важным свойством - отсутствием последствия. Несложно убедиться в том, что вероятность распада ядра за время при условии, что перед этим оно уже прожило время, совпадает с безусловной вероятностью распада того же самого ядра за время. Именно это свойство и представляет собой отсутствие последствия. 3) Равномерная на [a;b] непрерывная случайная величина(равномерное на отрезке [a;b] распределение).Равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок [a;b]. Закон Бернулли: число ожидаемых событий, появляющихся в опытах с n независимыми испытаниями, в которых ожидаемые события характеризуются одинаковой вероятностью p или: Математическое ожидание Пусть 6. смотри билет 5 Закон распределения Пуассона: удовлетворяет вероятности появления заданного количества редко происходящих случайных событий, наблюдаемых в серии из большого количества независимых повторных опытов. Вероятность намного меньше 1. Где m-число ожидаемых событий, а- параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма. Распределению Пуассона удовлетворяют числа редких событий, происходящих за определённый промежуток времени. 7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры. Дискретные случайные величины – величины, которые могут принимать счетное количество значений конечное или бесконечное. Непрерывные случайные величины- величины. Которые принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения Плотностью вероятности f(x) непрерывной случайной величины Х называется производная функции распределения F(X) этой величины: f(x)=F’(X) Основные свойства плотности: 3).определенный интеграл в пределах от минус бесконечности до плюс бесконечности от плоности вероятности непрерывной случайной величины равен единице.. 4)определенный интеграл в пределах от «–«бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины. Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ ² — дисперсия. Графики нормального распределения
8. Стандартное нормальное распределение. Стандартные интервалы. Понятия доверительного интервала и доверительной вероятности. Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью. Пусть (1)
выполняются с вероятностью (2) Обозначим
Интервал Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ ² — дисперсия. Графики нормального распределения
9. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативость. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки. Генеральная совокупность – множество каких-либо однородных элементов, которые предстоит изучить статистическими методами; множество всех значений случайной величины, а варианта – одно из значений генеральной совокупности. Выборка – это некоторая часть элементов, выделяемая по определенному правилу из ген. совокупности. Объём выборки – это число выделяемых элементов в генеральной совокупности. Минимальным, статистическим допустимым объёмом выборки, считается три элемента. Выборка производится с целью описания генеральной совокупности. Если это описание является полным и корректным, то выборка является репрезентативной. Результаты повторных измерений какой-либо физической величины х, проводимых в одинаковых условиях, часто называют выборкой из бесконечной генеральной совокупности, поскольку считается, что в опыте теоретически возможно произвести сколь угодно большое число измерений при одинаковых условиях, а множество всех возможных результатов измерений и образуют данную генеральную совокупность. Математическое ожидание такой генеральной совокупности считается истинным значением измеряемой величины.Таким образом, в ходе нескольких повторных измерений физической величины получают набор результатов, являющийся выборкой объёма n:х1, х2,…..,хn, где n-число повторных измерений.Как дискретные, так и непрерывные, случайные величины могут быть получены в результате опыта – наблюдения – то есть в виде вариационнго ряда: 4,67; 5,49; 5351 и так далее. Однако такой способ задания является малоинформативным – требующим дополнительной обработки, для какого-либо даже поверхностного представления о случайной величине. К выборочным характеристикам отнтсятся: · среднее значение (Хср), как оценка математического ожидания · выборочное среднеквадратическое отклонение (Sx), как оценка генерального значения среднеквадратического отклонения (σ) выборочная дисперсия (Sx2) N- число элементов выборки
№ 10 Точечные оценки параметров генеральной совокупности. .Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину
Величина Естественно считать величину Выборочную дисперсию
можно считать точечной оценкой дисперсии Dx генеральной совокупности. Приведем еще один пример точечной оценки. Пусть каждый объект генеральной совокупности характеризуется двумя количественными признаками x и y. Например, деталь может иметь два размера – длину и ширину. Можно в различных районах измерять концентрацию вредных веществ в воздухе и фиксировать количество легочных заболеваний населения в месяц. Можно через равные промежутки времени сопоставлять доходность акций данной корпорации с каким-либо индексом, характеризующим среднюю доходность всего рынка акций. В этом случае генеральная совокупность представляет собой двумерную случайную величину x,h. Эта случайная величина принимает значения x, y на множестве объектов генеральной совокупности. Не зная закона совместного распределения случайных величин x иh, мы не можем говорить о наличии или глубине корреляционной связи между ними, однако некоторые выводы можно сделать, используя выборочный метод. Выборку объема n в этом случае представим в виде таблицы, где
Выборочный коэффициент корреляции рассчитывается по формуле
Здесь
Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции rxh, характеризующего генеральную совокупность. Выборочные параметры Пусть выборочный параметр dрассматривается как выборочная оценка параметра D генеральной совокупности и при этом выполняется равенство M d = D. Такая выборочная оценка называется несмещенной. Для доказательства несмещённости некоторых точечных оценок будем рассматривать выборку объема n как систему n независимых случайных величин x1,x2,... x n, каждая из которых имеет тот же закон распределения с теми же параметрами, что и случайная величина x, представляющая генеральную совокупность. При таком подходе становятся очевидными равенства: Mxi = M x i = M x; Теперь можно показать, что выборочная средняя
Выведем формулу для дисперсии выборочной средней:
Найдем теперь, чему равно математическое ожидание выборочной дисперсии s 2. Сначала преобразуем s 2 следующим образом:
Здесь использовано преобразование:
Теперь, используя полученное выше выражение для величины s 2, найдем ее математическое ожидание.
Так как M s 2 ¹ D x, выборочная дисперсия не является несмещенной оценкой дисперсии генеральной совокупности. Чтобы получить несмещенную оценку дисперсии генеральной совокупности, нужно умножить выборочную дисперсию на
Пусть имеется ряд несмещенных точечных оценок одного и того же параметра генеральной совокупности. Та оценка, которая имеет наименьшую дисперсию, называется эффективной. Полученная из выборки объема n точечная оценка d n параметра D генеральной совокупности называется состоятельной, если она сходится по вероятности к D. Это означает, что для любых положительных чисел e и g найдется такое число neg, что для всех чисел n, удовлетворяющих неравенству n > neg выполняется условие Интервальные оценки. Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности оценок становится очень важным. Введем понятие интервальной оценки неизвестного параметра генеральной совокупности (или случайной величины x, определенной на множестве объектов этой генеральной совокупности). Обозначим этот параметр через D. По сделанной выборке по определенным правилам найдем числа D 1 и D 2, так чтобы выполнялось условие: P (D 1< D < D 2) =P (D Î(D 1; D 2)) = g Числа D 1 и D 2 называются доверительными границами, интервал (D 1, D 2) — доверительным интервалом для параметра D. Число g называется доверительной вероятностью или надежностью сделанной оценки. Сначала задается надежность. Обычно ее выбирают равной 0,95, 0,99 или 0,999. Тогда вероятность того, что интересующий нас параметр попал в интервал (D 1, D 2) достаточно высока. Число (D 1 + D 2) / 2 – середина доверительного интервала – будет давать значение параметра D с точностью (D 2 – D 1) / 2, которая представляет собой половину длины доверительного интервала. Границы D 1 и D 2 определяются из выборочных данных и являются функциями от случайных величин x 1, x 2,..., xn, а следовательно – сами случайные величины. Отсюда – доверительный интервал (D 1, D 2) тоже случаен. Он может покрывать параметр D или нет. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число D.
11. Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя). Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верх
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.013 с.) |

 n = n0
n = n0 


 Закон радиоактивного распада: число радиоактивных ядер, которые ещ не распались, убывает со временем по экспоненциальному закону:
Закон радиоактивного распада: число радиоактивных ядер, которые ещ не распались, убывает со временем по экспоненциальному закону: 

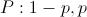


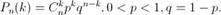
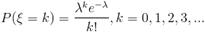 где -
где -  параметр.
параметр.
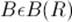
 где -
где -  интегрируемая по Лебегу функция. Функция
интегрируемая по Лебегу функция. Функция  называется плотностью распределения случайной величины.
называется плотностью распределения случайной величины.
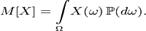
 — случайная величина, определённая на некотором вероятностном пространстве. Тогда
— случайная величина, определённая на некотором вероятностном пространстве. Тогда  где символ M обозначает математическое ожидание.
где символ M обозначает математическое ожидание.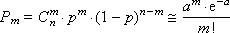



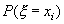 дискретной случайной величины
дискретной случайной величины  называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *
называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *  Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.
Пусть
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.
Пусть  — случайная величина, определённая на некотором вероятностном пространстве. Тогда
— случайная величина, определённая на некотором вероятностном пространстве. Тогда
 где символ M обозначает математическое ожидание.
где символ M обозначает математическое ожидание.
 - выборка из некоторого распределения с плотностью
- выборка из некоторого распределения с плотностью  , зависящей от параметра
, зависящей от параметра  , который может изменяться в интервале
, который может изменяться в интервале  . Пусть
. Пусть  - некоторая статистика и
- некоторая статистика и 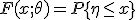 - функция распределения случайной величины
- функция распределения случайной величины  , когда выборка
, когда выборка  . Предположим, что
. Предположим, что  есть убывающая функция от параметра
есть убывающая функция от параметра  квантиль распределения
квантиль распределения  (например, 0,05 или 0,01). Пусть
(например, 0,05 или 0,01). Пусть  . При каждом
. При каждом 
 , близкой к единице. Перепишем неравенства (1) в другом виде:
, близкой к единице. Перепишем неравенства (1) в другом виде:
 ,
,  и запишем (2) в следующем виде:
и запишем (2) в следующем виде: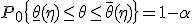
 называется доверительным интервалом для параметра
называется доверительным интервалом для параметра 
 называется относительной частотой значения признака xi. Если значения признака, полученные из выборки не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой
называется относительной частотой значения признака xi. Если значения признака, полученные из выборки не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой  .
. выборочной оценкой параметра M x. Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.
выборочной оценкой параметра M x. Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.

 ,
,  ,
, .
. или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами.
или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами. есть несмещенная оценка средней генеральной совокупности или, что то же самое, математического ожидания интересующей нас случайной величины x:
есть несмещенная оценка средней генеральной совокупности или, что то же самое, математического ожидания интересующей нас случайной величины x: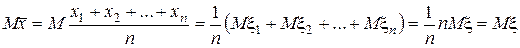 .
. .
.
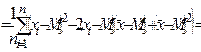





 .
. . Тогда получится величина
. Тогда получится величина  , называемая исправленнойвыборочнойдисперсией.
, называемая исправленнойвыборочнойдисперсией.
 .
.  являются несмещёнными, состоятельными и эффективными оценками величин Mx и Dx.
являются несмещёнными, состоятельными и эффективными оценками величин Mx и Dx.


