Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення курсової вартості та дохідності облігаційСодержание книги Поиск на нашем сайте
З погляду оцінки вартості і дохідності важливим є існування трьох типів облігацій – відсоткові (купонні), цільові та дисконтні. Незалежно від виду, типу та додаткових параметрів облігаційної позики в аспекті фінансової математики це лише певний потік платежів. По суті, будь-яка облігація – це зобов’язання емітента про виплату фіксованих сум грошей у фіксовані моменти часу в майбутньому. Отже, облігаційне зобов'язання описують такими параметрами: - номінальною вартістю (номіналом); - термін сплати основного боргу(термін погашення); - купонним доходом(купонною ставкою); - датами виплат відсотків(періодичністю купонних виплат). Сума майбутніх грошових потоків за купонними облігаціями складається з відсотків за фінансовим активом і ціни облігації на момент погашення. Для оцінки вартостікупонної облігації враховуються наступні показники: номінальна вартість, відсоткова ставка, строк до погашення, умови виплати відсотків (періодичність виплат). Таким чином, поточна ринкова вартість купонних облігацій при умові, що протягом строку обігу облігації здійснюються періодичні виплати відсотків, а в кінці строку виплачується номінал, розраховується за формулою:
(2.1) де С - річні купонні виплати; N - номінальна вартість облігації; r - ринкова відсоткова ставка у n-му періоді (дохідність до погашення облігації); t - кількість періодів до погашення облігації. Ця формула є базовою математичною моделлю оцінки грошової вартості відсоткових облігації. Дохідність до погашення (ставка дисконту) –це дохідність у розрахунку на рік, яку забезпечить собі інвестор, якщо купивши облігацію він буде тримати її до погашення. Найбільш важливим моментом при розрахунку вартості облігації є визначення ставки дисконтування. На практиці її можна взяти, наприклад, з котирувань, у брокерських компаній за облігаціями з подібними характеристиками. Її також можна спробувати визначити аналітично, розклавши ставку на складові частини. Ставку дисконтування можна визначити наступними чином:
(2.2) де r – ставка дисконтування, r 1 – премія за ліквідність, і – темп інфляції, r Наприклад, r Ставка без ризику (r При виплаті суми купону за облігаціями частіше ніж один раз на рік формулу визначення поточної вартості облігації можна трансформувати наступним чином:
(2.3) де k – періодичність виплат відсотків протягом року. У випадку коли вся сума відсотків виплачується при погашенні облігації, формула модифікується наступним чином:
де Сk - сума відсотків за облігацією, яка буде нарахована при її погашенні за відповідною ставкою. Для облігацій з нульовим купоном (дисконтних ) поточна ринкова вартість визначається за допомогою формули:
(2.5) де n - кількість років, через які відбудеться погашення облігації. Якщо строк обігу дисконтних облігацій менше одного року, то поточна ринкова вартість облігації визначається за формулою:
(2.6) де Т - кількість днів до погашення облігації. За безстроковими облігаціями передбачений невизначено тривалий період виплати доходів (купону). При умові фіксованого розміру купону протягом всього строку обігу облігації поточна ринкова вартість розраховується за нижче наведеною формулою і фактично представляє суму членів нескінченно спадаючої геометричної прогресії.
(2.7) Для оцінки ефективності вкладень в облігації використовуються наступні показники: купонна, поточна та повна дохідність. 1. Купонна ставка (Дс) встановлюється при емісії облігації, визначається відносно до номіналу і показує, який відсоток доходу нараховується щорічно власнику облігації. Купонна ставка розраховується за формулою:
(2.8) де С - річний купонний дохід, гр. од. Як правило, цей показник не розраховується, а встановлюється згідно умов випуску. 2. Поточна дохідність визначає відсоток доходу, який щорічно отримує власник облігації на інвестований капітал. Вона розраховується як відсоткове співвідношення між річним купонним доходом від облігації і тією ціною, за якою інвестор її придбав. Слід розрізняти дохідність, що наводиться у біржових зведеннях, і дохідність для певного інвестора: у першому випадку у знаменнику стоїть поточна вартість цінного паперу, у другому - використовується ціна, за якою інвестор купив облігацію. Таким чином поточна дохідність може бути визначена за формулою:
(2.9) де Р Поточна дохідність являє собою наче фотографію дохідності облігації на даний момент часу. У знаменнику формули стоїть поточна ціна облігації. У наступний момент вона може змінитися, тоді зміниться і значення поточної дохідності. 3. Дохідність до погашення (кінцева дохідність облігації) є більш об’єктивним показником дохідності, тому що при її визначенні враховуються не тільки купон і ціна паперу, але і період часу, який залишається до погашення, а також знижка або премія відносно номіналу. Дохідність облігації можна вивести з формули оцінки вартості купонної облігації:
(2.10) У деяких випадках для прийняття рішення достатньо визначити тільки орієнтовний рівень дохідності паперу. Формула визначення орієнтованої дохідності облігації має наступний вигляд:
(2.11) де r – дохідність до погашення, N - вартість реалізації (номінал) облігації, Р - ціна купівлі облігації (поточна вартість на момент оцінки), n - кількість років до погашення облігації, С – купон. Недоліком наведеної формули є те, що, якщо облігація продається зі знижкою, то формула дає занижене значення дохідності облігації, а якщо з премією, - завищене. Після того, як інвестор визначив значення дохідності облігації, він може скористатися формулою визначення точної цифри дохідності:
(2.12) Техніка розрахунку дохідності за формулою зводиться до наступного. Вкладник обирає значення r1, що нижче отриманого значення орієнтовної дохідності, і розраховує для нього відповідну ціну облігації Р1, скориставшись формулою оцінки вартості купонної облігації. Далі бере значення r2, що вище значення орієнтовної дохідності, і розраховує для нього ціну Р2. отримані значення підставляються в формулу визначення точної цифри дохідності. Наведені вище формули визначенні дохідності облігацій передбачали виплату купону один раз на рік. Відповідно у відповідях отримувалося значення r, що дорівнювало простому відсотку в розрахунку на рік. Якщо за облігацією купон виплачується m разів на рік, то можна скористатися вказаною формулою без всіляких корегувань, тобто не множити кількість років на m і не ділити купон на m. У цьому випадку ми також отримаємо дохідність паперу як простий відсоток у розрахунку на рік. У той самий час, можна визначити значення дохідності, здійснивши вказане корегування. Наприклад, для облігації, за якою купон виплачується два рази на рік, формула орієнтовної дохідності буде мати наступний вигляд:
(2.13) Однак у цьому випадку r є дохідністю за півроку. Щоб отримати дохідність за рік, необхідно отримане значення помножити на 2. Дохідність до погашення облігації з нульовим купоном визначається за формулою:
(2.14) Якщо більша частина купонних облігацій має купони, що виплачуються m разів на рік, то вищенаведену формулу необхідно скорегувати на величину m, тобто:
(2.15) Потрібно зазначити, що на практиці інвестора цікавить також питання про дохідність, яку він собі забезпечить, якщо продасть облігацію раніше строку погашення. Іншими словами, потрібно вміти розраховувати дохідність за період, яка визначається від відношення доходу, отриманого за облігацією за цей період, до сплаченої за нею суми. Рішення про купівлю тієї чи іншої купонної облігації у ряді випадків доцільно приймати на основі значення не дохідності до погашення, а на основі реалізованого відсотку. Він розраховується з урахуванням усіх надходжень, які інвестор зможе отримати за час користування облігацією. Загальна сума коштів, які вкладник отримає за облігацією, складається з трьох елементів: 1. Суми погашення при викупі облігації або суми від її продажу. 2. Купонних відсотків. 3. Відсотків від реінвестованих купонів. Якщо вкладник тримає облігацію до погашення, то перший елемент доходів відомий з умов випуску облігаційної позики. Другий елемент – купон – також відомий. Третій елемент можна визначити тільки у сукупності з другим за формулою майбутньої вартості ануїтету, а саме:
(2.16) де С С – купон облігації; n – кількість періодів, за які виплачуються купони; r – відсоток, під який вкладник планує реінвестувати купонні платежі. Реалізований відсоток – це відсоток, який дозволяє прирівняти суму всіх майбутніх надходжень, які інвестор планує отримати за облігацією, до її сьогоднішньої вартості. Він визначається за формулою:
(2.17) де: В – всі майбутні надходження; S - ціна придбання облігації. Реалізований відсоток дозволяє приймати рішення, виходячи з очікувань розвитку кон’юнктури ринку. До теперішнього часу ми визначали значення ціни і дохідності облігації, не враховуючи той факт, що за нею можуть сплачуватися податки і виплачуватися комісійні винагороди брокерським фірмам. Ці поправки легко зробити, скорегувавши формули визначення ціни та дохідності, розглянуті вище. Корегування формул полягає у тому, що отриманий прибуток зменшують на розмір стягнутих податків і на розмір сплачених комісійних. У якості витрат розраховується не тільки ціна, за якою купується папір, але і комісійні брокерської фірми.
(2.18) де: Tax – ставка податку на облігації; k – комісійні платежі як відсоток від суми угоди (розраховується у формулі у десяткових значеннях). Контрольні питання: 1. Наведіть моделі оцінки вартості облігацій. 2.Які показники використовуються для оцінки ефективності вкладень в облігації? 3.Назвіть фактори, що визначають інвестиційні якості облігацій? 4. Який показник за своїм змістом відображає внутрішню норму дохідності інвестицій вкладених у облігації? 3. Визначення курсової вартості та дохідності банківських сертифікатів і векселів При погашенні банківського сертифікату інвестор отримає суму нарахованих відсотків, що визначається за формулою:
(3.1) де N - номінал сертифікату, I - сума нарахованих відсотків, C% - купонний відсоток, T – час, на який випущений сертифікат. При погашенні сертифікату інвестору також повернуть суму номіналу паперу. Загальну суму, яку отримає вкладник при погашенні сертифікату, можна визначити за формулою:
(3.2) де S – сума відсотків і номіналу сертифікату. Вартість сертифікату визначається за формулою:
(3.3) де Р – вартість сертифікату, t r – дохідність, яку бажав би забезпечити собі інвестор. Дохідність сертифікату визначається за формулою:
(3.4) Дисконтні векселі котируються на основі ставки дисконту. Вона свідчить про величину знижки, яку продавець надає покупцю. Ставка дисконту вказується у відсотках до номіналу векселя як простий відсоток у розрахунку на рік. Ставку дисконту можна перерахувати у гривневий еквівалент за допомогою формули:
(3.5) де D – дисконт векселя, N – номінал векселя, d – ставка дисконту, t – кількість днів з моменту придбання векселя до його погашення. Ставка дисконту визначається за формулою:
(3.6) Ціну векселя можна визначити вирахувавши з номіналу розмір знижки, а саме: P=N-D, де P- ціна векселя. Якщо відома ставка дисконту, то ціна визначається за формулою:
(3.7) Якщо інвестор визначив для себе значення дохідності, яку б він хотів забезпечити за векселем, то ціну паперу можна обчислити за формулою:
(3.8) де r – дохідність, яку має намір забезпечити собі інвестор. Якщо вкладник порівнює інвестиції у вексель з іншими паперами, для яких фінансовий рік дорівнює 365 днів, то у формулу в знаменник доцільно ставити число 365. Ставка дисконту являє собою характеристику дохідності векселя. Однак вона не дозволяє безпосередньо порівнювати дохідність векселя з дохідністю інших цінних паперів, оскільки, по-перше, вона розраховується на базі 360 днів, і, по-друге, при її визначенні знижка ділиться на номінал, тоді як реально покупець інвестує меншу суму, а саме ціну. Ці обставини занижують дохідність векселя. Тому необхідно визначити формулу для перерахунку ставки дисконту і дохідність на базі 365 днів з урахуванням ціни. Її можна знайти з наступного рівняння:
(3.9) де r – еквівалентна ставка дохідності. Тоді
(3.10) Еквівалентну ставку також можна визначити з формули визначення ціни векселя, якщо взяти фінансовий рік у 365 днів:
(3.11) За відсотковим векселем нараховуються відсотки за ставкою, яка вказана у векселі. Суму нарахованих відсотків можна визначити за формулою:
(3.12) де І – сума нарахованих відсотків, N – номінал векселя, С
Контрольні питання: 1. Які показники використовуються для оцінки ефективності вкладень в банківські сертифікати? 2.Які існують моделі оцінки внутрішньої вартості векселів? 3. Назвіть фактори, що визначають інвестиційні якості банківських сертифікатів та векселів? 4.Що таке фактурні ціни?Як вони використовуються на фондовому ринку США для оцінки боргових цінних паперів?
Приклади: Приклад 1. Акціонерне товариство здійснило емісію привілейованих акцій номінальною вартістю 100 грн. з гарантованими дивідендними виплатами 20% на рік. Ставка дисконту – 12%. Розрахувати ціну привілейованої акції.
Приклад 2. Придбана інвестором акція є перспективною і буде використовуватися довгий час. На перші п’ять років ним складений прогноз дивідендів, згідно з яким у перший рік сума дивідендів складе 100 грн., а наступні роки буде щорічно зростати на 20 грн. Норма поточноїдохідності даного типу складає 15% на рік. Визначити поточну ринкову вартість акції.
Приклад 3. Компанія сплачує річні дивіденди у розмірі 17 грн. на акцію, норма поточної доходності по акціям даного типу складає 14%. Яка має бути вартість акції?
Приклад 4. Інвестор прогнозує, що у наступному році компанія отримає прибуток у розмірі 17 грн. на акцію. Частка прибутку, спрямованого на реінвестування складає 60%, необхідний рівень дохідності складає 14%. Прибуток, спрямований на розвиток виробництва, забезпечує отримання доходу у розмірі 18%.
Приклад5. Акція номіналом 1000 грн. куплена за курсом 250 грн., і по ній сплачується дивіденд 50% річних. Визначимо поточну дохідність інвестованих коштів. Ціна придбання акції за курсом 250 складає:
Абсолютний розмір дивіденду за ставкою 50%
Поточна дохідність паперу:
Це означає, що з кожного карбованця, вкладеного в акцію, інвестор отримав за рік 0,2 грн. доходу. Приклад 6. Інвестор придбав акцію номіналом 30 грн. за курсом 117% і продав через 4 роки за курсом 136%. У перший рік рівень дивідендів складав 2,4 грн. на акцію, у другий рік ставка дивіденду склала 10%, у третій рік відповідно – 11%, у четвертий рік рівень дивідендів склав 3,4 грн. Розрахуйте сукупну і середньорічну (кінцеву) дохідність акції. Дивіденди по роках склали відповідно: 1 рік = 2,4 грн. 2 рік = 30 грн.*0,1 = 3 грн. 3 рік = 30 грн.*0,11 = 3,3 грн. 4 рік = 3,4 грн. Р0 = 30*1,1 7= 35,1 грн.
Р1 = 30*1,36 = 40,8 грн.
Середньорічна сукупна доходність (кінцева) за короткостроковими операціями може бути розрахована за формулою:
де Р1 – вартість акції на момент продажу; Т – кількість днів володіння акцією. Приклад 7. Інвестор придбав акції ВАТ “Айстра” 18 вересня 2001 року за ціною 25,6 грн., продав 25 березня 2002 року за ціною 27,2 грн. 15 лютого інвестор отримав дивіденди у розмірі 1,6 грн. на акцію. Визначити середньорічну сукупну дохідність акції. Період володіння акціями (Т)= 12+31+30+31+31+28+25=188 днів
Приклад 8. Визначити вартість облігації, що випущена на 10 років, до погашення залишилося 4 роки. Номінальна вартість складає 200 грн., річна купонна ставка 18%, ринкова дохідність (ставка дисконтування) 12%.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.247 (0.008 с.) |

 ,
, - поточна вартість облігації з періодичною виплатою відсотків;
- поточна вартість облігації з періодичною виплатою відсотків; ,
, - ставка без ризику, тобто ставка за інвестиціями, для яких відсутній ризик; у якості такої ставки беруть дохідність за державними цінними паперами для відповідних строків погашення,
- ставка без ризику, тобто ставка за інвестиціями, для яких відсутній ризик; у якості такої ставки беруть дохідність за державними цінними паперами для відповідних строків погашення, - реальна ставка відсотку.
- реальна ставка відсотку.
 ,
, ,
, ,
,
 ,
, ,
, – поточна вартість облігації (ціна, за якою інвестор придбав облігацію).
– поточна вартість облігації (ціна, за якою інвестор придбав облігацію).
 ,
, .
. .
.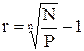
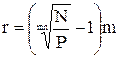
 ,
, - сума купонних платежів і відсотків від реінвестованих купонів;
- сума купонних платежів і відсотків від реінвестованих купонів; ,
, ,
,
 ,
, ,
, ,
,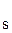 – кількість днів з моменту купівлі до погашення сертифікату,
– кількість днів з моменту купівлі до погашення сертифікату, .
. ,
,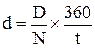 .
. .
. ,
, ,
, .
. .
. ,
,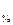 - відсоткова ставка, яка нараховується за векселем,
- відсоткова ставка, яка нараховується за векселем, - кількість днів від початку нарахування відсотку до його погашення.
- кількість днів від початку нарахування відсотку до його погашення.
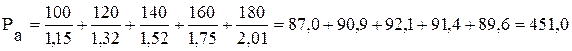


 грн.
грн.
 , або 20%.
, або 20%.