Разветвляющиеся и сливающиеся стрелки

Явные стрелки имеют источником одну-единственную работу и назначением тоже одну-единственную работу.

Однако одни и те же данные или объекты, порожденные одной работой, могут использоваться сразу в нескольких других работах. Тогда мы говорим о разветвляющейся стрелке.

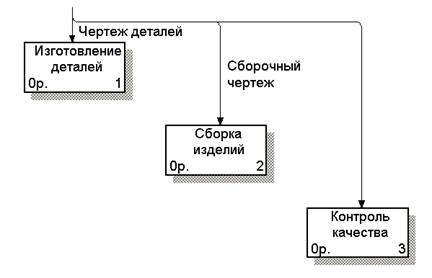
Рис. 4.9 Разветвляющаяся стрелка

С другой стороны, стрелки, порожденные в разных работах, могут представлять собой одинаковые или однородные данные или объекты, которые в дальнейшем используются или перерабатываются в одном месте. Для моделирования такой ситуации используются сливающиеся стрелки.

Смысл разветвляющихся и сливающихся стрелок передается именованием каждой ветви стрелок. Существуют определенные правила именования таких стрелок.

Правила именования для разветвляющихся стрелок.

1) Если стрелка именована до разветвления, а после разветвления ни одна из ветвей не именована, то подразумевается, что каждая ветвь моделирует те же данные или объекты, что и ветвь до разветвления.

2)
Если стрелка именована до разветвления, а после разветвления какая-либо из ветвей тоже именована, то подразумевается, что эти ветви соответствуют именованию. Если при этом какая-либо ветвь после разветвления осталась неименованной, то подразумевается, что она моделирует те же данные или объекты, что и ветвь до разветвления.

Рис. 4.10 Именование разветвляющихся стрелок

3)
Недопустима ситуация, когда стрелка до разветвления не именована, а после разветвления не именована какая-либо из ветвей.

Рис. 4.11 Недопустимая ситуация именования стрелок

Правила именования сливающихся стрелок полностью аналогичны. Недопустимой будет считаться ситуация, при которой стрелка после слияния не именована, а до слияния не именована какая-либо из ее ветвей.

Иерархия диаграмм модели и диаграмма дерева узлов

Иерархия диаграмм и контроль граничных стрелок

Модель SADT представляет собой серию диаграмм, разбивающую сложный объект на составные части, которые представляются в виде блоков. Детали каждого из основных блоков показаны в виде блоков на других диаграммах. Каждая детальная диаграмма является декомпозицией блока из более общей диаграммы. На каждом шаге декомпозиции более общая диаграмма называется родительской для более детальной диаграммы.

 

Рис. 4.12 Соответствие граничных стрелок

Стрелки, входящие в блок и выходящие из него на диаграмме верхнего уровня, являются точно теми же, что и стрелки, входящие в диаграмму нижнего уровня и выходящие из нее, потому что блок и диаграмма представляют одну и ту же часть системы.

Методология структурного анализа должна гарантировать правильное соединение всех диаграмм для образования согласованной модели. Для этого следует присвоить ICOM-коды граничным стрелкам новой диаграммы согласно правилам:

- представить рисунок новой диаграммы внутри декомпозируемого блока, продлить внешние стрелки до края диаграммы, соединить каждую внешнюю стрелку диаграммы с соответствующей граничной стрелкой декомпозируемого блока;

- присвоить код каждой связи, использовать I для входных стрелок, С – для стрелок управления, О – для выходных стрелок, М ‑ для механизмов;

- добавить после каждой буквы цифру, соответствующую положению данной стрелки среди других стрелок того же типа, причем входные и выходные стрелки пронумеровать сверху вниз, а стрелки управлений и механизмов слева направо.

Туннелирование стрелок

При построении диаграмм декомпозиции может возникнуть ситуация, когда отдельные стрелки высшего уровня не имеет смысла продолжать рассматривать на диаграммах нижнего уровня, или наоборот – отдельные стрелки нижнего уровня отражать на диаграммах более высоких уровней. Это будет только перегружать диаграммы, и делать их сложными для восприятия.

Для решения подобных задач предусмотрено понятие туннелирования. Обозначение туннеля в виде двух круглых скобок вокруг начала стрелки обозначает, что эта стрелка не была унаследована от функционального родительского блока и появилась из туннеля только на этой диаграмме.

В свою очередь, такое же обозначение вокруг конца стрелки в непосредственной близи от блока-приемника означает тот факт, что в дочерней по отношению к этому блоку диаграмме эта стрелка отображаться и рассматриваться не будет, т.е. уйдет в туннель.

Чаще всего бывает, что отдельные объекты и соответствующие им стрелки не рассматриваются на некоторых промежуточных уровнях иерархии. В таком случае они сначала погружаются в туннель, а затем при необходимости возвращаются из туннеля.

Рис. 4.13 Варианты туннелирования стрелок

Нумерация блоков и диаграмм

Все работы на диаграммах должны быть пронумерованы. Номер должен состоять из числа или префикса и числа. Обычно используют префикс А. Работа на контекстной диаграмме имеет номер 0 или А0. Работы на диаграмме декомпозиции первого уровня имеют номера 1, 2, 3, 4 (или А1, А2, A3, А4) и т. д. Работы на диаграмме декомпозиции нижнего уровня имеют номер родительской работы и очередной порядковый номер. Например, работы, которые представляют декомпозицию работы 3 (или A3), будут иметь номера 31, 32, 33, 34 (или А31, А32, А33, А34) и т. д.

Диаграммы нумеруются в соответствие с номерами работ, которые они декомпозируют. Контекстная диаграмма всегда имеет номер А-О, диаграмма декомпозиции контекстной диаграммы – номер А0, остальные диаграммы декомпозиции имеют номер, совпадающий с номером работы, декомпозиция которой представлена на данной диаграмме. Например, A1, A2, А21, А213 и т. д.

Диаграмма дерева узлов

Работа на любой диаграмме может быть далее описана диаграммой нижнего уровня, которая, в свою очередь, может быть далее детализирована с помощью необходимого числа диаграмм. Работа может иметь одну родительскую и несколько дочерних работ, образуя дерево. Такое дерево называют деревом узлов.

Диаграмма дерева узлов показывает иерархию работ в модели и позволяет рассмотреть всю модель целиком, но не показывает взаимосвязи между работами. Диаграмм деревьев узлов может быть в модели сколь угодно много, поскольку дерево может быть построено на произвольную глубину и не обязательно от корня.

На следующем рисунке показано типичное дерево диаграмм.

Рис. 4.14 Диаграмма дерева узлов