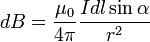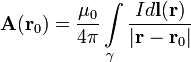Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая теория электропроводности металлов.Содержание книги
Поиск на нашем сайте
Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь
Предельная допустимая техническими нормами плотность тока для медных проводов составляет около Таким образом, даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в Работа электрического тока.
Закон Джоуля-Ленца. При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. 2.8. Магнитное взаимодействие. Магнитное взаимодействие — это взаимодействие упорядочение движущихся электрических зарядов. Магнитное поле. Магнитное поле - это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами. Сила Лоренца и сила Ампера. Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью
Сила Ампера - это сила, с которой магнитное поле действует на проводник с током.
Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индукции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике. Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику. Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю. Направление силы Ампера определяется по правилу левой руки. Индукция и напряженность магнитного поля.
Расчетная формула:
B - магнитная индукция
B - магнитная индукция
H - напряжённость магнитного поля
H - напряжённость магнитного поля
Закон Био-Савара-Лапласа. Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов. Формулировка Пусть постоянный ток
Направление
Векторный потенциал даётся интегралом (в системе СИ)
2.9.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.202 (0.009 с.) |

 . Правда в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле
. Правда в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле 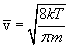 . Для комнатной температуры (
. Для комнатной температуры (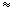 300К) вычисление по этой формуле приводит к следующему значению:
300К) вычисление по этой формуле приводит к следующему значению: 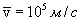 . При включении поля на хаотическое тепловое движение, происходящее, со скоростью
. При включении поля на хаотическое тепловое движение, происходящее, со скоростью 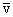 , накладывается упорядоченное движение электронов с некоторой средней скоростью
, накладывается упорядоченное движение электронов с некоторой средней скоростью 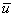 . Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью
. Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью 
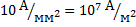
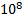 раз меньше средней скорости теплового движения
раз меньше средней скорости теплового движения 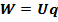
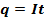
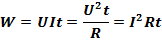
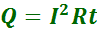
 положительный заряд (здесь
положительный заряд (здесь 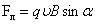
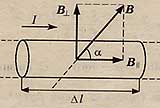

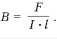 Магнитная индукция - векторная физическая величина, характеризующая магнитное поле. Вектор магнитной индукции всегда направлен по касательной к магнитной линии
Магнитная индукция - векторная физическая величина, характеризующая магнитное поле. Вектор магнитной индукции всегда направлен по касательной к магнитной линии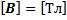
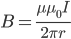 Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током
Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током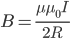
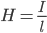 Напряженностью магнитного поля называют векторную величину
Напряженностью магнитного поля называют векторную величину 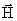 , характеризующую магнитное поле и определяемую следующим образом:,
, характеризующую магнитное поле и определяемую следующим образом:, 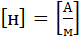
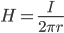 Напряжённость магнитного поля: бесконечной прямой провод
Напряжённость магнитного поля: бесконечной прямой провод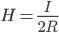 Напряжённость магнитного поля в центре витка
Напряжённость магнитного поля в центре витка течёт по контуру γ, находящемуся в вакууме,
течёт по контуру γ, находящемуся в вакууме,  —точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
—точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)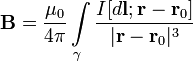
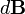 перпендикулярно
перпендикулярно 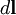 и
и 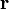 , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление
, то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление