
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання до практичної роботи №1Содержание книги
Поиск на нашем сайте
1. Побудувати графік порівняння показників якості двох виробів за шкалою інтервалів та за шкалою відношень. Вихідні дані вибрати згідно варіанта із таблиці 1.4. 2. Визначити якість продукції комплексним методом. 3. Зробити висновок щодо рівня якості порівнюваної продукції. Таблиця 1.4 – Варіанти завдань до практичної роботи №1
Для варіантів 16-30 за показники базової моделі прийняти дані варіанту 1, для варіантів 31-45 за показники базової моделі прийняти дані варіанту 2. ПРАКТИЧНА РОБОТА №2 СТАТИСТИЧНІ МЕТОДИ УПРАВЛІННЯ ЯКІСТЮ ПРОДУКЦІЇ Мета роботи Ознайомлення з одним із статистичних методів управління якістю продукції Матеріальне забезпечення ДСТУ ІСО 9004-4-98 "Управління якістю та елементи системи якості. Частина 4. Настанови щодо поліпшення якості". . Теоретичні відомості Статистичні методи являються важливою умовою рентабельного управління якістю, а також засобом підвищення ефективності виробничих процесів і якості продукції. У стандартах ІСО 9001 - ІСО 9003, в яких розглядаються системи якості, записано: "У разі потреби постачальник повинен розробляти процедури, що забезпечують вибір статистичних методів, необхідних для перевірки можливості технологічного процесу і прийнятності характеристик продукції". Для вирішення проблем, пов'язаних з якістю продукції, широко використовуються 7 традиційних методів (так званих "інструментів" якості), а саме: контрольні листки, контрольні карти, діаграми розсіювання, гістограми, діаграми Парето, причинно-наслідкові діаграми, часові ряди. На сьогодні ці методи, набувши подальшого розвитку, стандартизовані та рекомендуються для використання в роботі по підвищенню якості (міжнародний стандарт ІСО 9004-4: 1993). В Україні прийнятий ДСТУ ІСО 9004-4-98 "Управління якістю та елементи системи якості. Частина 4. Настанови щодо поліпшення якості". Як зазначає відомий японський спеціаліст з якості професор К.Ісікава: "Базуючись на досвіді своєї діяльності, можу сказати, що 95% усіх проблем фірми можуть бути вирішені за допомогою цих семи прийомів". Для контролю якості необхідно зібрати певні дані, а потім їх обробити. Але дані, що характеризують навіть один і той же параметр виробу, не можуть бути багаторазово отримані за ідентичних умов, тому що в процесі виробництва змінюються окремі деталі та обставини. Тому при операціях з контролю якості мають справу з великим числом даних, які характеризують ті чи інші параметри виробу, умови процесу тощо. Ці дані при повторних вимірюваннях завжди дещо відрізняються від отриманих в інший час і за інших умов, тобто завжди спостерігається розкидання даних, аналізуючи яке можна знайти вирішення проблеми, що виникла в процесі виробництва. Наприклад, при використанні тієї ж самої технології та однакових виробничих операцій, в одному випадку виробляється якісний виріб, в іншому - неякісний. Якщо порівняти процес виготовлення якісного та неякісного виробів, детально вивчаючи дані щодо кожного етапу, процесу, можна виявити момент, коли відмінність в даних є максимальною. Таким чином можна знайти причину, що призвела до появи браку. Усунення причини або системи причин і буде рішенням проблеми. Систематизація, обробка та дослідження такого великого числа даних за допомогою різноманітних методів з метою виявлення визначених закономірностей, яким вони підкоряються, називається статистичною обробкою; дані при цьому називаються статистичними даними, а методи, що застосовуються - статистичними методами. Як правило, для обробки й аналізу даних використовують не один, а декілька статистичних методів. Це інколи дає змогу отримати цінну інформацію, яка при аналізі розкидання даних лише одним методом може висковзнути. Найбільш поширеним статистичним методом управління якістю вважається побудова гістограми з подальшою математичною обробкою отриманих даних. Гістограма – це стовпчиковий графік, побудований згідно з отриманими даними, які розбиваються на кілька інтервалів. Число даних, що потрапляють до кожного з інтервалів виражається висотою стовпчика. Розглянемо побудову гістограми на конкретному прикладі. Необхідно побудувати гістограму розсіювання розмірів партії деталей, що складається із 50 штук та визначити ймовірний відсоток придатних деталей та відсоток виправного і невиправного браку. Вимірювання проводились із точністю до 0,1мм. Розміри придатних до використання деталей знаходяться в межах: - найбільший 8,0 мм, найменший 7,0 мм. Значення розмірів для побудови гістограми взяті із таблиці 2.1.
Таблиця 2.1 – Вихідні дані
1. Визначаємо найбільше L та найменше S значення даних: L=9,0; S=7,0. 2. Розраховуємо кількість інтервалів. Кількість інтервалів повинно приблизно відповідати квадратному кореню з числа даних. Так, як у нас 50 даних, то кількість інтервалів вибираємо рівним семи. 3. Розраховуємо ширину інтервала h. Для цього різницю між L та S ділимо на кількість інтервалів і заокруглюємо в більшу сторону. h = (9,0 – 7,0)/7 = 0,28 мм. Приймаємо h=0,3мм. 4. Визначаємо значення границь інтервалів. За початок першого інтервалу приймаємо значення S. Додаючи до отриманого значення ширину ділянки h = 0,3 мм, знаходимо, що перша ділянка займає інтервал на осі абсцис від 7,0 мм до 7,3 мм. Аналогічно, додаючи 0,3 мм до 7,3 мм, отримаємо інтервал другої ділянки 7,3 – 7,6 мм. і т.д. До інтервалу останньої ділянки входить найбільше значення L. 5. Розраховуємо середні значення для інтервалів. Середнє значення для інтервалу визначають за формулою: (нижня границя інтервалу + верхня границя інтервалу)/2. У даному випадку середнє значення для першого інтервалу хі = (7,0 + 7,3)/ 2 = 7,15. Середні значення наступних інтервалів знаходяться додаванням ширини інтервалу h = 0,3 мм до значення попередньої ділянки. 6. Будуємо графік гістограми. По осі абсцис відкладаємо межі інтервалів, а по осі ординат – частоту. Для кожного інтервалу будуємо прямокутник (стовпчик) з основою, яка дорівнює ширині інтервалу, висота його відповідає кількості деталей, що попали в цей інтервал. На рисунку dmax та dmin найбільший та найменший розмір придатних до використання деталей
 
7,0 7,3 7,6 7,9 8,2 8,5 8,8 9,1 Рисунок 2.1-Гістограма Математичну обробку результатів побудови гістограми зручно звести до таблиці 2.2. Таблиця 2.2 –Обробка результатів побудови гістограми
7. Використовуючи таблицю 2 знаходимо середнє значення відхилень
8. Знаходимо середнє квадратичне значення відхилень випадкових розмірів
9. Розраховуємо значення х1 та х2 – межі допуску відносно середнього значення відхилень та значення z1 і z2 за формулами:
10. За таблицею функції Лапласа знаходимо значення Ф(z1) та Ф(z2). Значення функції Лапласа вибираємо із довідкової літератури. Ф(z1)=0,49 Ф(z2)=0,001 11. Знаходимо ймовірний відсоток придатних деталей F, та виправного і невиправного браку що складають: F = F1 + F2 = (Ф(z1) + Ф(z2)) 100%=49+0,1=49,1% брак виправний = (50% – F2)=49,9% брак невиправний = (50% – F1)=1%
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 51; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.195.254 (0.007 с.) |


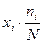
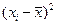

 випадкових розмірів і значення дисперсії D(x):
випадкових розмірів і значення дисперсії D(x):
 .
. за формулою:
за формулою: .
. ;
; .
.


