
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение частот вращения и крутящих моментов на валахСодержание книги
Поиск на нашем сайте Привода Частоты вращения валов: n1 = nточн = 2940 (об/мин) (1.7) n2 = n1/uкр = 2940/3.15 = 933.33 (об/мин) (1.8) n3 = nвых = 230 (об/мин) (1.9) Крутящие моменты: T1 = Tвых/(η∙uп) = 610/(0.885∙12.783) = 53.92 (Нм) (1.10) T2 = T1∙uкр/(ηкр·ηПК) = 53.92∙3.15/(0.95∙0.99) = 180.6 (Нм) (1.11) T3 = 610 (Нм) (1.12) Мощности: N1 = Nдв = 18.5 (кВт) (1.13) N2 = N1·ηкр·ηпк = 18.5·0.95·0.99 = 17.4 (кВт) (1.14) N3 = N2·ηпк·ηп·ηм = 17.4·0.99·0.97∙0.98 = 16.375 (кВт) (1.15) Т а б л и ц а 1.2 – Параметры валов привода
Требуемая долговечность привода Требуемую долговечность определим по формуле: L = 8760∙Л∙Кс = 8760∙4∙0.67 = 23477 (часов) (1.16) где Л = 4 – количество лет работы привода; Кс =0.67 – коэффициент сменности работы привода для работы в 2 смены.
Расчет передач привода Расчет передачи редуктора Выбор материалов и термообработки В качестве материла для шестерни принимаем сталь 40Х, улучшение; твердость 269…302 HB. Для зубчатого колеса сталь 40ХН, улучшение; твердость 235…262 HB [2]. Определение допускаемых контактных напряжений Допускаемые контактные напряжения для шестерни [sH]1 или колеса [sH]2:
где SH – коэффициент безопасности (SH1 = 1.1, SH2 = 1.1); sH0 – предел контактной выносливости (sH01 = 640 МПа, sH02 = 567 МПа); ZN – коэффициент, учитывающий ресурс и режим работы, определяемый из условия для шестерни или колеса, находится в пределах 1 ZN 2.6 при SH = 1,1:
где NH0 – базовое число циклов перемены напряжений, определяемое по формуле: NH0 = 30×HB2,4 £ 12×107; (2.3) NHE – эквивалентное число циклов, соответствующее: NHE = NH×KHE = 60×nw×n×L, (2.4) где nw – число зацеплений, в которое входит шестерня или колесо за один оборот, в нашем случае nw = 1; n – соответствующая частота вращения, мин-1; L – ресурс привода, час; При nш = 933.33 об/мин и nк = 230 об/мин, L = 23477 ч находим эквивалентное число циклов для шестерни и колеса: NHE1 = 60×nw×nш×L = 60·1·933.33·23477 = 131.5·107, (2.5) NHE2 = 60×nw×nк×L = 60·1·230·23477 = 32.4·107; (2.6) Зная твердость поверхности зубьев шестерни и колеса, найдем базовое число циклов перемены напряжений: NH01 = 30×HB2,4 = 30·2852.4 = 2.34·107, (2.7) NH02 = 30×HB2,4 = 30·2482.4 = 1.67·107 (2.8) При NH0 < NHE принимаем Найдем допускаемые контактные напряжения:
Допускаемые контактные напряжения для передачи принимаем по минимальному значению: [sH] = 515 (МПа). Определение допускаемых изгибных напряжений Допускаемые напряжения изгиба определяются для шестерни [sF]1 и колеса [sF]2 по формуле:
где sF0 – предел изгибной выносливости (sF01 = 514 МПа, sF02 = 447 МПа); SF – коэффициент безопасности (SF1 = SF2 = 1.7); YА – коэффициент, учитывающий влияние двухстороннего приложения нагрузки. В нашем случае, YА = 1; YR – коэффициент, учитывающий шероховатость переходной кривой. YR = 1 при шероховатости RZ £ 40 мкм. YN – коэффициент, учитывающий срок службы передачи и переменность режима нагружения, рассчитываемый по формуле:
где NF0 – базовое число циклов (для сталей NF0 = 4×106); NFE – эквивалентное число циклов: NFE = NHE (п. 2.2) Принимаем YN1 = YN2 = 1 из условия 1 £ YN < 2,5, поскольку NF0 < NFE; Определим допускаемые напряжения изгиба для шестерни [sF]1 и колеса [sF]2:
Геометрический расчет Межосевое расстояние определяется по формуле [2, 26]:
где Кнв = 1.04 - коэффициент концентрации напряжений [2, 27], [σH] = 515 МПа - допускаемое контактное напряжение (п. 2.2.2), Ψbа = 0.315 [1, 17] Eпр = E = 2.1·105 МПа для стали. Принимаем aw = 200 мм. Определим модуль передачи: m = (0.01…0.02)·aW = (0.01…0.02)·200 = 2…4 (2.16) Принимаем m = 3 [1, 21]. Определение числа зубьев: zΣ = 2aw/m = 2·200/3 = 133 (2.17) Определим числа зубьев шестерни и зубчатого колеса: z1 =zΣ/(u+1) = 133/(4.06 + 1) = 26.3, (2.18) принимаем z1 = 26, тогда: z2 = zΣ - z1 = 133 - 26 = 107 (2.19) Фактическое передаточное число UФ: UФ = z2/z1 = 107/26 = 4.12 (2.20) Делительные диаметры [1,31]:
d1 = 3∙26 = 78 (мм) (2.22) d2 = 3∙107 = 321 (мм) (2.23) Диаметр окружности вершин: dA1 = d1 + 2m = 78 + 2∙3 = 84 (мм) (2.24) dA2 = d2 + 2m = 321 + 2∙3 = 327 (мм) (2.25) Диаметр окружности впадин: df1 = d1 – 2.5m = 78 – 2.5∙3 = 70.5 (мм) (2.26) df2 = d2 – 2.5m = 321 – 2.5∙3 = 313.5 (мм) (2.27) Ширина зубчатого венца, не менее: bw = Yba∙aw = 0.4∙200 = 80 (мм), (2.28) примем ширину зубчатого колеса: b2 = 100 (мм), (2.29) Ширина шестерни: b1= b2 + (2..5) = 100 + (2…5) = 102…105 (мм) (2.30) Проверка зубьев на выносливость по контактным Напряжениям При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия
где
принимаем 8 степень точности зубчатой передачи. Тогда
Условие
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.218 (0.009 с.) |

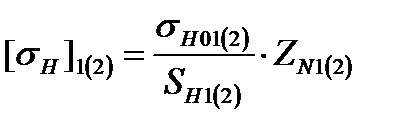 (МПа), (2.1)
(МПа), (2.1) , (2.2)
, (2.2)
 (2.9)
(2.9) (2.10)
(2.10) , (2.11)
, (2.11) (1 £ YN < 2,5), (2.12)
(1 £ YN < 2,5), (2.12) (2.13)
(2.13) (2.14)
(2.14) (мм) (2.15)
(мм) (2.15) (2.21)
(2.21) :
:
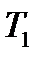 = 259∙103 - крутящий момент на шестерне, Нмм;
= 259∙103 - крутящий момент на шестерне, Нмм; - коэффициент расчётной нагрузки,
- коэффициент расчётной нагрузки,  ;
; - коэффициент концентрации нагрузки (п.2.1);
- коэффициент концентрации нагрузки (п.2.1); - угол зацепления,
- угол зацепления,  = 20;
= 20; - коэффициент динамической нагрузки, находят по [2,34] с понижением на одну степень точности против фактической, назначенной по окружной скорости [2,33]:
- коэффициент динамической нагрузки, находят по [2,34] с понижением на одну степень точности против фактической, назначенной по окружной скорости [2,33]: (м/с), (2.32)
(м/с), (2.32) , получаем:
, получаем: (2.33)
(2.33)


