
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение параметров газа в изоэнтропическомСтр 1 из 8Следующая ⇒
ГИПЕРЗВУКОВЫЕ ТЕЧЕНИЯ ГАЗОВ Изменение параметров газа в изоэнтропическом Гиперзвуковом потоке Течения газа со скоростью, значительно превосходящей скорость звука, называемые иногда гиперзвуковыми течениями, обладают рядом отличительных особенностей. Выразим в явном виде влияние изменения скорости течения На основные параметры газа. В единичной струйке газа при отсутствии потерь и внешней работы, согласно уравнению Бернулли, имеем
Отсюда с помощью известного выражения для скорости звука получаем соотношение, связывающее изменение давления с изменением скорости,
Уравнение сохранения теплосодержания струйки при адиабатическом течении можно представить в виде
После несложных преобразований отсюда следует
Дифференцируя уравнение состояния идеального газа и используя предыдущие соотношения, получаем аналогичную зависимость для изменения плотности
Дифференцируя равенство
Соотношения (1)—(4) показывают, что при дозвуковых скоростях (М <1) происходит незначительное изменение давления, плотности и температуры газа с изменением скорости, а число Маха зависит от скорости линейно. Наоборот, при гиперзвуковых скоростях ( При
Исключая из (1) и (5) множитель го ряда был отброшены. Из (2) и (5) аналогичным путем выводится зависимость температуры от числа Маха
Откуда следуют соответствующие выражения для скорости звука
И плотности газа
Интегрируя выражение (5), устанавливаем связь между скоростью потока и числом Маха
При выводе уравнения (10) функция В выражениях (6)—(10) величины без индексов соответствуют текущим значениям параметров газа, а величины с индексом «н» - их начальным значениям.
Гиперзвуковое течение около выпуклого тупого угла Рассмотрим особенности течения с очень большой скоростью около выпуклого тупого угла -гиперзвукового течения Прандтля—Майера (рис. 1). Секундная масса газа между произвольной линией тока и полюсом течения 0 постоянна и может быть вычислена по нормальной к характеристике составляющей скорости, которая равна скорости звука
Ия потока около выпуклого угла. ма отклонен Рис. 1. Схе Отсюда после дифференцирования имеем
Угол Маха (между линией тока и характеристикой) в случае гиперзвуковой скорости (
Если
Здесь принимается во внимание, что направления отсчета углов Из рис. 1. видно, что
так как при
Подставляя (14) в (11), имеем
Откуда на основании (2), (3) и (5) получаем
Интегрируя это уравнение и учитывая соотношения (12) и (13) при условии, что начальному значению
здесь
и подставляя это значение в выражения (6)—(10), получим формулы для определения текущих значений давления, плотности, температуры, скорости звука и скорости потока при гиперзвуковом обтекании выпуклого тупого угла. Плоская ударная волна в гиперзвуковом течении Остановимся теперь на соотношениях, характеризующих плоскую ударную волну, возникающую при обтекании с гиперзвуковой скоростью вогнутого тупого угла. В плоской косой ударной волне изменение плотности будет
Здесь Зависимость угла отклонения потока в ударной волне от угла наклона фронта
Рис. 2. Схема отклонения потока в ударной волне. Заменяя
В достаточно интенсивных скачках уплотнения (
При любом сколь угодно малом фиксированном значении угла отклонения потока
Рис. 3. Зависимость коэффициентов сопротивления Из равенства (19)
Из равенства (20)
При малом угле атаки Полученные в §§ 2 и 3 выражения дают возможность вывести простые формулы для коэффициентов подъемной силы и лобового сопротивления пластины, обтекаемой газовым потоком большой сверхзвуковой скорости при малом угле атаки. Спереди тел Рис. 4. Распределение давлений при обтекании потоком с большой сверхзвуковой Эта особенность гиперзвуковых течений получила название закона плоских сечений, с помощью которого нетрудно определить лобовое сопротивление тела, равное работе расширения соответствующей формы эквивалентного поршня, совершаемой над газом в слое за время прохождения тела сквозь этот слой. Контур поршня в каждый момент времени и нормальная скорость его точек определяются формой тела, а давление на его поверхности отыскивается из решения соответствующей задачи о неустановившемся движении газа. Закон сопротивления Ньютона Значительный накопленный опыт показывает, что для расчета сопротивления тела при гиперзвуковом обтекании можно использовать закон сопротивления Ньютона, полагавшего, что движущаяся жидкость состоит из одинаковых частиц, заполняющих равномерно пространство и не взаимодействующих друг с другом; при столкновении с телом частицы теряют нормальную к поверхности тела составляющую количества движения (неупругий удар), вследствие чего появляется сила давления потока на тело. Избыточное давление жидкости на участки тела, расположенные позади его наибольшего поперечного сечения, т. е. в аэродинамической тени (рис. 5), Ньютон считал равным нулю. Аэродинамическая тень
Рис. 5. Обтекание тела, соответствующее модели Ньютона Если элемент поверхности тела площадью
Однако практический расчет распределения давлений по поверхности тела, обтекаемого гиперзвуковым потоком, с помощью закона Ньютона дает во многих случаях удовлетворительные результаты несмотря на то, что влияние вязкости в теории Ньютона не учитывается.
Рис. 6. Распределение давления по окружности конуса, обтекаемого потоком под углом атаки. Сравнение формулы Ньютона и экспериментальных данных. На рис. 6. показано безразмерное давление
ТЕЧЕНИЯ РАЗРЕЖЕННЫХ ГАЗОВ При нормальном давлении величина свободного пробега молекул составляет миллионные доли сантиметра. При понижении плотности газа свободный пробег молекул возрастает обратно пропорционально плотности, и если он становится соизмеримым с характерными размерами потока, то дискретная структура газа начинает сказываться на законах газовой динамики и Теплообмена. Число Кнудсена можно выразить через известные критерии подобия - числа Маха М и Рейнольдса связывающую кинематическую вязкость со свободным пробегом и средней скоростью движения молекул
Средняя скорость молекул выражается через скорость звука
Тогда из (2) и (3) имеем
Нольдса
где х - длина тела. Поэтому если речь идет о гидродинамическом трении или теплообмене, когда характерным размером является толщина пограничного слоя (
При малых значениях числа Рейнольдса (
Имеющиеся теоретические и экспериментальные данные свидетельствуют о том, что при очень малых значениях числа Кнудсена ( При очень больших значениях числа Кнудсена (
Переходная область между режимом со скольжением и свободно-молекулярным режимом остается до сих пор мало изученной, так как в ней приходится учитывать как столкновения молекул между собой, так и неоднократные столкновения их с телом, а это создает большие теоретические трудности.
Рис. 1. Границы различных режимов течения разреженного газа. Таблица 1
Сопоставляя данные рис. 1 и таблицы 1, можно получить представление о связи между высотой полета и границами различных режимов. Для ракеты длиной 3 м влияние скольжения начинает проявляться с высоты 50 км при Рис. 2. Профиль скорости у стенки при течении со скольжением. Учитывая изложенное, можно определить среднюю направленную скорость слоя газа непосредственно у стенки, исходя из того, что этот слой состоит наполовину из молекул, приходящих к стенке, и наполовину из отраженных от нее
Таблица 2
Ввиду того что доля диффузно отраженных молекул близка к единице (
Отсюда следует, что в плотном газе ( Таким образом, уточненное граничное условие, характеризующее скачок скорости у стенки, должно иметь следующий вид:
Вторым членом соотношения (11), учитывающим температурный крип, чаще всего можно пренебречь, так как при высоких продольных градиентах температуры и очень больших разрежениях, когда этот член особенно существен, обычно реализуется свободно-молекулярное течение газа без гидродинамического пограничного слоя. Однако в некоторых специальных случаях (например, обтекание головной части ракеты во время входа ее, в сравнительно плотные слои атмосферы) условие (11) используется в полном виде. Таблица 3
Рис. 3. Ламинарное течение газа со скольжением В трубе. Здесь мы пренебрегли малой величиной изменения количества движения в направлении оси трубы, которое вызывается изменением плотности газа, обусловленным в свою очередь изменением давления. Выражая напряжения трения по формуле Ньютона, из (13) имеем
Отсюда после интегрирования в граничных условиях, учитывающих скорость скольжения на стенке (
На оси трубы (при
Это дает следующую окончательную зависимость для безразмерного профиля скорости в трубе при скольжении:
Напряжение трения на стенке
Для скорости у стенки
Где
- значение коэффициента трения в начале трубы. Используя уравнение состсяния для идеального газа, из (26) получаем дифференциальное уравнение
Отсюда следует
где
Подставим в (27)
Имея и виду, что
получим при
Где
Решение (28) справедливо лишь при
Рис. 4. Зависимость коэффициента трения при течении со скольжением в трубе от числа Она хорошо согласуется с опытными данными Кнудсена и других исследователей. Горизонтальные участки кривых При наличии скольжения Впервые влияние скольжения на сопротивление тела было обнаружено Милликеном в 1911 г. при исследовании скорости падения мелких масляных капель в воздухе под действием силы тяжести, а также скорости подъема против силы тяжести заряженных капель, находящихся в вертикально направленном электростатическом поле. Рис. 5. Функции распределения для Движение молекул сказывается на макроскопических свойствах газа. Давление газа на стенку можно определить как силу, которая возникает в результате изменения нормальной к стенке составляющей суммарного количества движения молекул при их соударении со стенкой; при этом молекулу и стенку считают абсолютно упругими твердыми телами. Расположим стенку по нормали к оси абсцисс (рис. 6.) и определим количество молекул, которое встретится с элементарной площадкой размером
где
Рис. 6. К определению числа молекул, встречающихся со Стенкой за единицу времени. Формулу для определения величины давления:
Или
где
Или в соответствии с (35)
Так как было принято, что импульс ударяющихся о стенку молекул равен импульсу отраженных молекул, то полученная величина давления складывается из двух равных частей: давления ударяющихся и давления отраженных молекул
Где
В первых работах Энштейна и Смолуховского, посвященных свободно-молекулярному течению газа около твердого тела, предполагалось, что скорость упорядоченного движения газа мала по сравнению со средней скоростью хаотического движения молекул. Мы не станем пользоваться этим ограничением и приведем решение задачи для произвольного значения числа Маха в набегающем на тело газовом потоке. Как показал Цзян, такое общее решение имеет достаточно простой вид. Обтекание тела разреженным газом целесообразно рассматривать в прямоугольной системе координат, так как при этом удобно группируются одноименные составляющие скоростей хаотического и упорядоченного движении. Если газ сильно разрежен, то столкновения молекул между собой и с поверхностью тела настолько редки, что реэмитируемые поверхностью молекулы практически не возмущают набегающий на тело невозмущенный поток газа и не нарушают максвелловского распределения хаотических скоростей (
Рис. 7. К определению силы Определяя аэродинамические силы, которые возникают на единичной площадке тела при свободно-молекулярном обтекании, следует иметь в виду, что проекция аэродинамической силы равна разности проекций на ту же ось количеств движения секундной массы молекул, падающих на площадку и отраженных от нее. И напряжение трения
При полностью диффузном отражении молекул от стенки (
Расчет аэродинамических сил Рис. 8. К определению аэродинамических сил на пластине Рис. 9. К определению расхода газа в трубе при молекулярном течении. вырежем в поперечном сечении 2 трубы элементарную площадку Пусть отражающий молекулы элемент поверхности трубы площадью площадки Окончательная формула для секундного расхода газа при свободно-молекулярном течении по длинной круглой трубе имеет следующий вид:
И в конечном сечении трубы
Величина
И через короткую трубку Рассмотрим свободно-молекулярное перетекание газа через отверстие радиуса
Рис. 10. К расчету молекулярного истечения через отверстие в стенке. Пусть толщина стенки ГИПЕРЗВУКОВЫЕ ТЕЧЕНИЯ ГАЗОВ Изменение параметров газа в изоэнтропическом Гиперзвуковом потоке
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.82.23 (0.122 с.) |
 .
.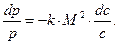 (1)
(1)
 (2)
(2) (3)
(3) и выражая скорость звука через температуру газа, находим соотношение
и выражая скорость звука через температуру газа, находим соотношение . (4)
. (4)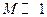 ) даже небольшое изменение скорости течения ведет к заметному изменению состояния газа и числа Маха.
) даже небольшое изменение скорости течения ведет к заметному изменению состояния газа и числа Маха. (5)
(5) и выполняя интегрирование, получаем характерную для гиперзвуковых течений зависимость давления от числа Маха
и выполняя интегрирование, получаем характерную для гиперзвуковых течений зависимость давления от числа Маха (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) была разложена в ряд по степеням
была разложена в ряд по степеням 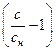 , причем ввиду близости отношения
, причем ввиду близости отношения  к единице все нелинейные члены это
к единице все нелинейные члены это .
.
 . (11)
. (11) . (12)
. (12) - угол отклонения потока от первоначального направления, а
- угол отклонения потока от первоначального направления, а  - угол между заданной характеристикой и первоначальным направлением потока, то очевидно,
- угол между заданной характеристикой и первоначальным направлением потока, то очевидно,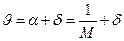 , (13)
, (13) и
и  , (14)
, (14) .
. ,
,
 .
. отвечает
отвечает  , получаем для гиперзвукового течения следующую связь между числом Маха и углом отклонения потока:
, получаем для гиперзвукового течения следующую связь между числом Маха и углом отклонения потока: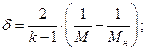 (15)
(15) и
и  - текущее и начальное значения числа Маха. Разрешая уравнение (15) относительно текущего значения числа Маха
- текущее и начальное значения числа Маха. Разрешая уравнение (15) относительно текущего значения числа Маха (15а)
(15а) (18)
(18)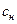 .
.
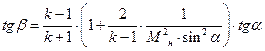 . (19)
. (19) - угол между вектором скорости за ударной волной и фронтом последней.
- угол между вектором скорости за ударной волной и фронтом последней. , после элементарных преобразований получаем
, после элементарных преобразований получаем (22)
(22) ) всегда имеет место неравенство
) всегда имеет место неравенство . (23)
. (23) можно достичь такого значения числа Маха, при котором условие (23) будет выполнено. Следовательно, в соотношениях (18)—(22) можно пренебречь членами
можно достичь такого значения числа Маха, при котором условие (23) будет выполнено. Следовательно, в соотношениях (18)—(22) можно пренебречь членами  и тогда окажется, что безразмерные значения возмущении скорости
и тогда окажется, что безразмерные значения возмущении скорости  ,
,  , безразмерная плотность
, безразмерная плотность  и угол наклона фронта скачка
и угол наклона фронта скачка  (и температуры
(и температуры  ) пропорциональны величине
) пропорциональны величине  :
: (24)
(24) , (28)
, (28) и
и  . (29)
. (29)
 наклонен к набегающему потоку под углом
наклонен к набегающему потоку под углом  , а нормальная («потерянная») составляющая скорости есть
, а нормальная («потерянная») составляющая скорости есть  , поэтому нормальная составляющая силы давления по закону Ньютона
, поэтому нормальная составляющая силы давления по закону Ньютона , (37)
, (37)
 в различных точках поверхности конуса с центральным углом 20°
в различных точках поверхности конуса с центральным углом 20°  , обтекаемого потоком воздуха с
, обтекаемого потоком воздуха с  под углом атаки
под углом атаки  . Кривая на рис. 6. рассчитана по формуле Ньютона (38). Как видим, экспериментальные точки лежат достаточно близко к теоретической кривой.
. Кривая на рис. 6. рассчитана по формуле Ньютона (38). Как видим, экспериментальные точки лежат достаточно близко к теоретической кривой.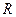 ; для этого следует использовать формулу Чепмена из кинетической теории газов,
; для этого следует использовать формулу Чепмена из кинетической теории газов, :
: (2)
(2)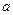
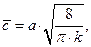 где
где  . (3)
. (3)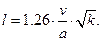 (4)
(4)
 ), то при
), то при  согласно (5), число Кнудсена становится пропорциональным отношению числа Маха к корню квадратному из числа Рейнольдса
согласно (5), число Кнудсена становится пропорциональным отношению числа Маха к корню квадратному из числа Рейнольдса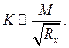 (6)
(6) ) толщина пограничного слоя сравнима с длиной тела (
) толщина пограничного слоя сравнима с длиной тела ( ), поэтому
), поэтому (7)
(7) ) газ ведет себя как сплошная среда. В интервале значений числа Кнудсена
) газ ведет себя как сплошная среда. В интервале значений числа Кнудсена  можно также пользоваться уравнениями газовой динамики сплошной среды, однако при этом, как будет показано ниже, следует в граничные условия на твердой поверхности вводить поправку на так называемые «скольжение» и «скачок температуры».
можно также пользоваться уравнениями газовой динамики сплошной среды, однако при этом, как будет показано ниже, следует в граничные условия на твердой поверхности вводить поправку на так называемые «скольжение» и «скачок температуры». ) пограничный слой у поверхности тела не образуется, так как реэмитированные (отраженные) поверхностью тела молекулы сталкиваются с молекулами внешнего потока на далеком от него расстоянии, т. е. тело не вносит искажений в поле скоростей внешнего потока. Для этого режима «свободно-молекулярного течения газа», который по имеющимся данным наблюдается при
) пограничный слой у поверхности тела не образуется, так как реэмитированные (отраженные) поверхностью тела молекулы сталкиваются с молекулами внешнего потока на далеком от него расстоянии, т. е. тело не вносит искажений в поле скоростей внешнего потока. Для этого режима «свободно-молекулярного течения газа», который по имеющимся данным наблюдается при  , трение и теплообмен на поверхности обтекаемого тела рассчитываются из условия однократного столкновения молекул газа с поверхностью.
, трение и теплообмен на поверхности обтекаемого тела рассчитываются из условия однократного столкновения молекул газа с поверхностью.
 , м
, м




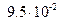
 и 30 км при
и 30 км при  . Свободно-молекулярное течение устанавливается при любой скорости полета, начиная с высоты 140 км.
. Свободно-молекулярное течение устанавливается при любой скорости полета, начиная с высоты 140 км.
 ), имеем приблизительно
), имеем приблизительно (10)
(10)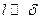 ) скольжение практически отсутствует (
) скольжение практически отсутствует ( ), т. е. молекулы «прилипают» к стенке, как это и принято в обычной газодинамике; в сильно разреженном газе (
), т. е. молекулы «прилипают» к стенке, как это и принято в обычной газодинамике; в сильно разреженном газе (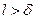 ) скорость скольжения близка к скорости невозмущенного потока газа вне пограничного слоя (
) скорость скольжения близка к скорости невозмущенного потока газа вне пограничного слоя ( ). При течении со скольжением скорость у стенки подчиняется условию (9), которое обычно заменяют приближенным условием (10).
). При течении со скольжением скорость у стенки подчиняется условию (9), которое обычно заменяют приближенным условием (10). (11)
(11)
 (14)
(14) и
и  ), получаем
), получаем
 ) имеем
) имеем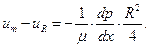
 (15)
(15) (17)
(17) (22)
(22)

 (27)
(27) - полная длина трубы. В этом решении один корень отброшен (с отрицательным знаком) как не отвечающий физическим условиям задачи (
- полная длина трубы. В этом решении один корень отброшен (с отрицательным знаком) как не отвечающий физическим условиям задачи ( при
при  ). Если вычитаемое под корнем значительно меньше единицы, то справедливо приближенное решение, позволяющее определить падение давления в трубе без учета сжимаемости газа
). Если вычитаемое под корнем значительно меньше единицы, то справедливо приближенное решение, позволяющее определить падение давления в трубе без учета сжимаемости газа . (28)
. (28) , а также на основании (5) значение
, а также на основании (5) значение

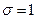
 (29)
(29) .
. . Зависимость коэффициента трения
. Зависимость коэффициента трения  от числа Рейнольдса при различных значениях числа Маха представлена на рис. 4.
от числа Рейнольдса при различных значениях числа Маха представлена на рис. 4.
 отвечают переходу к свободно-молекулярному течению (
отвечают переходу к свободно-молекулярному течению (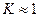 ).
). ; в течение одной секунды об эту площадку ударится половина от всего количества молекул данной скорости, заполняющих цилиндр с образующей
; в течение одной секунды об эту площадку ударится половина от всего количества молекул данной скорости, заполняющих цилиндр с образующей 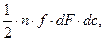 (36)
(36)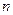 - полное число молекул в единице объема,
- полное число молекул в единице объема, 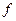 - значение функции, соответствующее скорости
- значение функции, соответствующее скорости 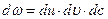 - элемент пространства скоростей.
- элемент пространства скоростей.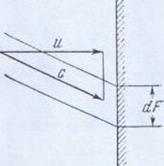

 ,
, - средняя квадратичная скорость движения молекул в направлении нормали к стенке. Так как при хаотическом движении все направления равнозначны
- средняя квадратичная скорость движения молекул в направлении нормали к стенке. Так как при хаотическом движении все направления равнозначны
 .
.
 .
.

 ) молекул в этом газе. Функция распределения Максвелла может быть представлена в виде
) молекул в этом газе. Функция распределения Максвелла может быть представлена в виде (40)
(40) (50)
(50)
 (51)
(51) и длиной
и длиной 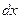 находится в сечении 1, отстоящем от сечения 2 на расстоянии х, а радиус-вектор ВА, соединяющий
находится в сечении 1, отстоящем от сечения 2 на расстоянии х, а радиус-вектор ВА, соединяющий и составляет угол
и составляет угол  с осью трубы.
с осью трубы. (60)
(60) . (63)
. (63) (64)
(64) в стенке (рис. 10.), по обе стороны которой даьлспи/;, температуры и илотноии ггиа исодииакииы.
в стенке (рис. 10.), по обе стороны которой даьлспи/;, температуры и илотноии ггиа исодииакииы.



