
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В таких случаях при малых углах заострения тела и малых углах атаки основной критерий
подобия представляет собой произведения числа Маха набегающего потока поверхности тела к набегающему потоку) или относительная толщина тела Это подтверждается опытными данными, приведенными на рис. 4, на котором изображены кривые безразмерных значений избыточного давления на поверхности цилиндра с оживальной головной частью, полученные при разных значениях числа Маха и для различных величин относительной толщины оживальной части (при нулевом угле атаки). Как видим кривые распределения давлений универсальны при Область действия закона подобия для гиперзвукового обтекания тонкого тела оживальной формы приблизительно определяется следующими границами:
Область применимости закона подобия значительно расширяется, если в качестве критерия подобия вместо величины
Рис. 4. Распределение давлений при обтекании потоком с большой сверхзвуковой Скоростью аффинно-подобных тел. Выше было показано, что при гиперзвуковом обтекании тонкого тела продольное возмущение скорости ничтожно
Иначе говоря, тонкое тело раздвигает слои обтекающего его газа таким образом, как будто в каждом слое (независимо от соседних слоев) происходит вытеснение газа непроницаемым подвижным поршнем в направлении, перпендикулярном к направлению движения тела. Если всю область обтекания разбить плоскостями, перпендикулярными к скорости набегающего потока на множество слоев, то в каждом из них будет наблюдаться неустановившееся движение, вправленное только параллельно этим плоскостям.
Эта особенность гиперзвуковых течений получила название закона плоских сечений, с помощью которого нетрудно определить лобовое сопротивление тела, равное работе расширения соответствующей формы эквивалентного поршня, совершаемой над газом в слое за время прохождения тела сквозь этот слой. Контур поршня в каждый момент времени и нормальная скорость его точек определяются формой тела, а давление на его поверхности отыскивается из решения соответствующей задачи о неустановившемся движении газа. Закон сопротивления Ньютона Значительный накопленный опыт показывает, что для расчета сопротивления тела при гиперзвуковом обтекании можно использовать закон сопротивления Ньютона, полагавшего, что движущаяся жидкость состоит из одинаковых частиц, заполняющих равномерно пространство и не взаимодействующих друг с другом; при столкновении с телом частицы теряют нормальную к поверхности тела составляющую количества движения (неупругий удар), вследствие чего появляется сила давления потока на тело. Избыточное давление жидкости на участки тела, расположенные позади его наибольшего поперечного сечения, т. е. в аэродинамической тени (рис. 5), Ньютон считал равным нулю. Аэродинамическая тень
Рис. 5. Обтекание тела, соответствующее модели Ньютона Если элемент поверхности тела площадью
|
|||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.108.18 (0.005 с.) |
 на некоторый характерный угол
на некоторый характерный угол  . Под
. Под  (угол наклона
(угол наклона (отношение максимального поперечного размера к длине тела), так как в случае тонкого тела эти величины пропорциональны. Тонкие заостренные тела, у которых критерий
(отношение максимального поперечного размера к длине тела), так как в случае тонкого тела эти величины пропорциональны. Тонкие заостренные тела, у которых критерий  будем в дальнейшем называть аффинно-подобными. Ясно, что сохранение аффинно-подобного обтекания тела при изменении угла атаки
будем в дальнейшем называть аффинно-подобными. Ясно, что сохранение аффинно-подобного обтекания тела при изменении угла атаки  достигается в том случае, если последний пропорционален характерному углу тела, т. е. при условии
достигается в том случае, если последний пропорционален характерному углу тела, т. е. при условии 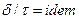 . Итак, относительные величины скоростей, коэффициенты аэродинамических сил и другие факторы, характеризующие гиперзвуковое обтекание тонкого тела, сохраняют свои значения, если не изменяются величины
. Итак, относительные величины скоростей, коэффициенты аэродинамических сил и другие факторы, характеризующие гиперзвуковое обтекание тонкого тела, сохраняют свои значения, если не изменяются величины  и
и  .
. и
и  , если выдерживается условие аффинного подобия:
, если выдерживается условие аффинного подобия:  .
.

 .
.
 , а поперечная скорость пропорциональна углу наклона поверхности тела
, а поперечная скорость пропорциональна углу наклона поверхности тела .
.
 наклонен к набегающему потоку под углом
наклонен к набегающему потоку под углом  , то масса газа, в которой происходит потеря количества движения, равна
, то масса газа, в которой происходит потеря количества движения, равна  , а нормальная («потерянная») составляющая скорости есть
, а нормальная («потерянная») составляющая скорости есть  , поэтому нормальная составляющая силы давления по закону Ньютона
, поэтому нормальная составляющая силы давления по закону Ньютона , (37)
, (37)


