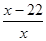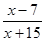Заняття 1. Історія виникнення поняття відсотка

АВТОРСЬКА ПРОГРАМА З ТЕМИ

«ВІДСОТКИ»

Структура програми

Програма містить:

- Пояснювальну записку.

- Мета, завдання курсу.

- Методичне забезпечення.

- Навчально-тематичний план.

- Зміст програми.

Пояснювальна записка

У наш час розуміння відсотків і уміння виконувати відсоткові розрахунки потрібні кожній людині: прикладне значення цієї теми дуже велике і пов’язане з багатьма сферами нашого життя, саме з фінансовою, соціологічною та іншими. Так як тема «Відсотки» пов'язує між собою багато точних і природничих наук, то вона показує учням зв’язок математики та інших наук.

Тема «Відсотки» розпорошено висвітлена в підручниках математики. Задачі на відсоткові розрахунки незначними групами розміщені в підручниках різних класів, без урахування вікових можливостей учнів. Вивчення цієї теми в основній школі є нетривалим, а учні через вікові особливості ще не можуть отримати повноцінні уявлення про відсотки, про їх роль в повсякденному житті. На наступних етапах навчання повторного звернення до цієї теми не передбачається. У багатьох шкільних підручниках можна зустріти завдання на відсотки, проте в них відсутнє компактне і чітке викладання теоретичних відомостей.

Текстові завдання на відсоткові розрахунки включені в зовнішнє незалежне оцінювання, в ДПА за курс неповної середньої школи та в завдання підсумкових робіт за курс середньої школи.

Проте завдання на відсотки досить часто викликають утруднення у школярів. Тому дана програма створена для об'єднання отриманих знань учнів в цілісну систему і для демонстрування учням застосування математичного апарату до розв'язання повсякденних завдань кожної людини. Матеріал даного курсу допоможе закріпити вміння пов'язані з відсотковими обчисленнями і сформувати стійкий інтерес до навчання.

Використання її можливе в 11 класі, як повторення матеріалу перед ЗНО, або ж як факультативний курс, чи для підготовки учнів до олімпіад тощо. Деякі заняття з цієї програми можна використовувати з учнями починаючи з 8 класів для формування практичних навичок застосування отриманих знань з теми «Відсотки» в житті.

Дана навчальну програма курсу «Відсотки» складена у відповідності з навчальною програмою математики (5-6 класи) і алгебри та відповідно до вимог державного освітнього стандарту основної загальної освіти з математики.

Цей курс передбачає чіткий виклад теоретичних питань, розв’язування типових завдань, завдань з практичним змістом, а саме таких завдань, які пов'язані із застосуванням відсоткових обчислень в повсякденному житті. Пропоновані завдання різні по рівню складності: від простих вправ на застосування вивчених формул до прийомів розрахунку відсотків в реальних ситуаціях (наприклад, обчислення банківських ситуації).

Пропонований курс спрямований на те, щоб надати учням додаткові знання по відсоткові обчислення для використання їх не лише в навчально-пізнавальному процесі, але і повсякденному житті – при розрахунку вигідності банківської угоди, рентабельності бізнесу, комерційної пропозиції.

У рамках курсу пропонується розв’язання завдань, пропонованих на ЗНО, ДПА та на математичних олімпіадах.

Цей курс «Відсотки» сприятиме не лише виробленню умінь і закріпленню навичок розв’язання різних завдань, пов'язаних з відсотковими розрахунками, але і формуванню інтересу учнів до математики, сприяти їх інтелектуальному розвитку.

Клас	Тема	Учень/учениця повинні
	Відсотки	формулювати означення відсотка, знаходити відсотки від числа та число за його відсотками;
	Відсоткове відношення двох чисел. Відсоткові розрахунки.	Розв’язувати три основні задачі на відсотки; записувати відсотки у вигляді звичайного і десяткового дробів; побудувати та аналізувати стовпчасті діаграми, аналізувати кругові діаграми.
В інших класах тема відсотки окремо не виділяється, а задачі на відсотки розглядаються в інших змістових лініях ШКМ.

Завдання курсу:

- повторити і систематизувати знання про відсотки;

- створити основу для розв’язання більш складних завдань, які пов’язують зміст шкільного курсу математики з життям;

- сприяти інтелектуальному розвитку учнів, формуванню логічного мислення, розвитку практичних здібностей.

Мета курсу:

- актуалізувати раніше вивчений і новий матеріал для забезпечення учням високого рівня знань по цій темі;

- сформувати уміння виконувати відсоткові розрахунки, необхідні для застосування в практичній діяльності і в завданнях з суміжних дисциплін, зокрема з «Основ економіки»;

- підготувати учнів до ДПА чи ЗНО;

- підвищити інтерес до вивчення математики.

В результаті курсу учні повинні:

- розуміти змістовний сенс терміну «відсоток» як спеціального способу вираження долі величини;

- знати широту застосування процентних обчислень в житті;

- уміти застосовувати формули «простих» і «складних» відсотків, знаходження відсотків від числа чи числа за його відсотками, формули відсоткового вмісту речовини;

Способи організації діяльності учнів на різних уроках:

- на уроках-лекціях учні вчаться конспектувати, аналізувати вивчені нові методи розв’язування завдань;

- на уроках-бесідах спільними зусиллями учителі і учнів вирішуються ключові завдання;

- на уроках-практикумах учні самостійно вирішують завдання, домагаючись тих або інших навичок, аналізують помилки і шляхи їх виправлення;

- на уроках-семінарах учні розповідають про виконану роботу, скажімо, про рішення якихось завдань з домашньої роботи, оцінюють розв’язання, оцінюють свою діяльність та діяльність інших.

 

Методичне забезпечення

Даний курс складається з теоретичної і практичної частин.

Форми організації навчання: індивідуальна, групова, колективна, взаємне навчання, самонавчання (при цьому вчитель контролює, корегує і направляє роботу учнів) Використовується: бесіда, лекція, консультація, практичне заняття, захист проекту, ділова гра.

Засоби навчання: довідкова література (наприклад з економіки), дидактичні матеріали (наприклад статистичні відомості), творчі завдання для групової роботи, мультимедійні засоби.

Технології навчання: інформаційні, модульне навчання, різнорівневі навчання, дослідницькі методи. Заняття носять проблемний характер. Передбачаються відповіді на питання в процесі дискусії, пошук інформації по суміжних галузей знань.

Кількість годин: вивчення спецкурсу розраховане на 17 години, орієнтовно 2 години в тиждень, кількість годин може змінюватись відповідно до бажань і потреб вчителя і учнів.

.

 

 

Навчально-тематичний план

№	Теми	Кількість годин
1.	Історія виникнення поняття відсотка
2.	Знаходження відсотків від числа і числа за його відсотками
3.	Завдання на суміші, сплави, концентрацію і відсотковий вміст
4.	Розв’язання завдань за допомогою рівнянь і нерівностей
5.	Завдання на відсотки в економіці
6.	Олімпіадні завдання
7.	Відсотки на ДПА та ЗНО
8.	Відсотки в нашому житті
9.	Заліковий урок

Форма контролю

Підсумкова оцінка за курс може проводитися у формі письмової контрольної роботи.

Зміст програми

Тема 1. Історія виникнення поняття відсотка (1 год.)

Заняття 1. Історія виникнення поняття відсотка

Форма проведення заняття: бесіда з використанням мультимедійних засобів (так як учні знайомі з даним матеріалом з курсу математики 5-6 класів, то дане заняття проводиться у формі бесіди для повторення і систематизації знань з даної теми).

Прийоми і методи: роз'яснення; роз`язування завдач за означенням.

Тема 2. Знаходження відсотків від і числа за його відсотками (2 год.)

Самостійна робота

Дана самостійна робота контрольного характеру. На написання самостійної роботи відводиться 20 хв.

Варіант 1

1. Значення якого з наведених виразів потрібно обчислити, щоб знайти 42% від 75?

А	Б	В	Г
75:100 42	100:75 42	42:75 100	75:42 100

 

2. Знайдіть 9% від числа 24.

А	Б	В	Г
21,6	2,16	2,6	20,6

 

3. Площа парку становить 42 га. Озеро займає 35% цієї площі. Яка площа озера?

А	Б	В	Г
12,4 га	16,5 га	15,6 га	14,7 га

 

4. Руда містить 8% міді. Скільки тон міді міститься в 250 т цієї руди?

А	Б	В	Г
2 т	20 т	200 т	0,2 т

5. До магазину завезли 1600 кг овочів, з них 27% складають огірки, 42% – картопля, а решту капуста. Скільки кілограмів капусти завезли до магазину?

6. Сергійко з батьком і матір’ю збирали гриби. Батько зібрав 46% відсотків усіх грибів, мати 32%, а Сергійко – решту 44 гриби. Скільки грибів всього зібрала сім’я?

7*Один множник збільшили на 10%, а другий зменшили на 10%. Як змінився добуток цих чисел?

 

Варіант 2

1. Знайдіть 28% від числа 96.

А	Б	В	Г
26,8	26,88	2,8	3,4

2. Значення якого з наведених виразів потрібно обчислити, щоб знайти 33% від 67?

А	Б	В	Г
33:67 100	100:33 42	67:100 33	67:33 100

 

 

3. У книжці, яку читає Катя 250 сторінок. Вона прочитала 18% всієї книжки. Скільки сторінок прочитала Катя?

А	Б	В	Г

 

4. Слав містить містить 12% алюмінію. Скільки кг алюмінію міститься в 370 кг сплаву?

А	Б	В	Г
42,4 кг	28,7 кг	4,44 кг	44,4 кг

5. Бригада трактористів зорала поле площею 480 га за два дня. За перший день вона зорала 45% поля. Скільки гектарів зорала бригада за другий день?

6. Спортивні змагання тривали три дні. Першого дня в них узяли участь 34% всіх учасників, другого дня – 30%, а третього – решта 108 спортсменів. Скільки всього було учасників змагання?

7.* На скільки відсотків збільшиться площа квадрата, якщо його сторону збільшити на 20%.

Розв’язання самостійної роботи

Варіант 1

А	Б	Г	В

№ 5

1) 100% – (27% + 42%) = 31% – складає капуста;

2) 1600:100·31 = 496 (кг) – капусти привезли до магазину.

Відповідь: 496 кг

№ 6

3) 100% – (46% + 32%) = 22% – зібрав Сергійко;

4) 44:0,22 = 200 (шт.) – грибів зібрала сім’я.

Відповідь: 200 грибів

№ 7*

Нехай перший множник а, після збільшення він стане а + 0,1а =1,1а і другий множник b, після зменшення 1 b - 0,1 b = 0,9 b. Початковий добуток був а b. Після зміни множників добуток стане 1,1 а ∙0,9 b = 0,99∙ а b.

Отже, 1∙а b - 0,99∙а b = 0,01∙а b. А так як 0,01 = 1%, то добуток зменшиться на 1%.

Відповідь: добуток зменшиться на 1%.

Варіант 2

Б	В	А	Г

№ 5

5) 480·0,45 = 216 (га) – зорала бригада;

6) 480 – 216 = 264 (га) – зорала бригада за 2 день.

Відповідь: 496 кг

№ 6

7) 100% – (34% + 30%) = 36% – становили 108 спортсменів;

8) 108:0,36 = 300 (осіб) – всього спортсменів.

Відповідь: 300 спортсменів

№ 7*

Початкова площа квадрата зі стороною а рівна а∙а, отже, після збільшення сторони матимемо таку площу квадрата 1,2а∙1,2а = 1,44∙а∙а. Очевидно, що площа збільшилася на (1 - 1,44)∙100% = 44%.

Відповідь: площа збільшиться на 44%.

 

 

Тема 3. Завдання на суміші, сплави, концентрацію і відсотковий вміст (3 год.)

Заняття 4, 5 (спарені уроки). Завдання на суміші, сплави, концентрацію і відсотковий вміст

Форма заняття: семінар-практикум

Спочатку учні обговорюють теоретичні питання, а потім переходять до виконання різних задач. На цьому уроці можна запропонувати учням пов’язати знання хімії і математики, писати не назви елементів, а їх хімічні формули.

Заняття 6. Завдання на суміші, сплави, концентрацію і відсотковий вміст

Форма заняття: семінар-практикум

Напередодні учні отримують карточки із виразом, який є розв’язанням задачі, їм потрібно скласти до нього задачу. На уроці ж учні презентують кожен свої задачу.

Тема 4. Розв’язання завдань за допомогою рівнянь і нерівностей (1 год.)

Заняття 14. Відсотки на ЗНО

Форма проведення занять: консультація, самостійна робота

Так як завдання на ЗНО дублюють завдання на ДПА, то учні працюють в парах, консультуючи один одного. Учитель допомагає їм. Пишуть самостійну роботу.

Учні відпрацьовують навики застосування здобутих знань на завданнях, які зустрічаються в ЗНО.

Заняття 17. Залік

Форма проведення занять: контрольна робота

Учні пишуть контрольну роботу у формі. Дана робота проводиться з метою діагностики якості знань з теми «Відсотки» і виставлення підсумкової оцінки і орієнтована на завдання в ДПА І ЗНО.

 

Варіант 1

1. На клумбі росли троянди і лілеї, причому лілеї становили 8% усіх квітів. Скільки відсотків усіх квітів становили троянди?

А	Б	В	Г
80%	40%	90%	88%

 

2. Знайдіть1% від 6 гривень?

А	Б	В	Г
6 коп	60 коп	6 грн	600 грн

 

3. Математичний гурток відвідують 40 учнів, 35% яких становлять дівчатка. Скільки дівчаток відвідують математичний гурток?

А	Б	В	Г
16 дівчаток	14 дівчаток	15 дівчаток	12 дівчаток

 

4. Рибалка спіймав 14 лящів, що становлять 28% усього вилову. Скільки всього риби спіймав рибалка?

А	Б	В	Г
200 рибин	28 рибин	50 рибин	72 рибини

 

№ 5

У будинку 51 двокімнатна квартира, що становить 17% усіх квартир. Скільки квартир у будинку?

№ 6

До їдальні привезли 150 кг овочів. Капуста становила 48% усіх овочів, морква – 24%, а картопля – решту. Скільки кілограмів картоплі завезли до їдальні?

№ 7

За перший місяць відремонтували 65% дороги, за другий – 60% остачі, а за третій – решту 28 км. Скільки кілометрів дороги відремонтували за три місяці?

№ 8*

У 100 кг сплаву міді і цинку вміст міді складає 45%. Скільки кг чистого цинку потрібно додати до сплаву, щоб кількість міді склала 20 % кількості цинку?

Варіант 2

1. У вазі стояли ромашки і волошки. Причому волошки становили 15% усіх квітів. Скільки відсотків усіх квітів становили ромашки?

А	Б	В	Г
50%	90%	85%	5%

 

2. Знайдіть1% від 2 метрів?

А	Б	В	Г
200 м	2 м	20 см	2 см

 

3. У класі навчається 25 учнів, 60% яких відвідують математичний гурток скільки. Скільки учнів відвідують математичний гурток?

А	Б	В	Г
10 учнів	12 учнів	17 учнів	15 учнів

 

4. У фінал вийшли 24 конкурсанти, що становить 12% усіх учасників конкурсу. Скільки осіб брали участь у конкурсі?

А	Б	В	Г
200 осіб	88 осіб	48 осіб	150 осіб

 

№ 5

У розчині міститься 140 г солі. Чому дорівнює маса розчину, якщо вміст солі в ньому становить 35%

№ 6

Потрібно відремонтувати 140 км дороги. За перший місяць відремонтували 36% дороги, за другий – 34%, а за третій – решту. Скільки кілометрів дороги відремонтували за третій місяць?

№ 7

За перший день було продано 60% завезеної до магазину тканини, за другий – 35% остачі, а за третій – решту 78 м. скільки метрів тканини завезли до магазину?

№ 8*

У сплав магнію і алюмінію, що містить 22 кг алюмінію, додали 15 кг магнію, після чого вміст магнію підвищилася на 33 %. Скільки важив сплав спочатку?

Варіант 1

В	А	Б	В

№ 5

51: 0,17 = 300 (г) – маса розчину

Відповідь: 300 г

№ 6

Всі овочі – 100%.

1) 100% – (48% + 24%) = 28% – завезли картоплі;

28% = 0,28

150 · 0,28 = 42

Отже, завезли 42 кг картоплі.

Відповідь: 42 кг.

№7

Нехай вся дорога – х км, тоді за перший місяць відремонтували 0,65 х км.

1) (х – 0,65 х) · 0,8 = 0,35 х · 0,6 = 0,21 х – відремонтували за 2 день;

2) 0,4 х – 0,14 х = 0,26 х – відремонтували за 3 день;

0,14 х = 28

х = 2800: 14

х = 200 (км)

Отже, відремонтували 200 км дороги.

Відповідь: 200 км

№ 8

Склад речовини	I	II
С		100 + х
К	0,45	0,2
М		0,2(100 + х)

 

45 = 0,2(100 + х); х = 125кг

Відповідь: 125 кг.

Варіант 2

В	Г	Г	А

№ 5

(140: 35) · 100 = 400 (г) – маса розчину

Відповідь: 400 г

№ 6

Вся дорога – 100%.

2) 100% – (36% + 34%) = 30% – відремонтували за 3 місяціь

30% = 0,3

140 · 0,3 = 42

Отже, відремонтували 42 км дороги.

Відповідь: 42 км

№7

Нехай до магазину привезли х м тканини, тоді за перший день продали 0,6 х м.

3) (х – 0,6 х) · 0,35 = 0,4 х · 0,35 = 0,14 х – продали за 2 день;

4) 0,4 х – 0,14 х = 0,26 х – продали за 3 день;

0,26 х = 78

х = 7800: 26

х = 300 (м)

Отже, завезли 300 м тканини.

Відповідь: 300 м

№ 8

Склад речовини	I	II
С	х	15 + х
К
М	х - 22	х - 7

 

– = 0,3.

х = 25.

Відповідь: 25 кг.

 

 

АВТОРСЬКА ПРОГРАМА З ТЕМИ

«ВІДСОТКИ»

Структура програми

Програма містить:

- Пояснювальну записку.

- Мета, завдання курсу.

- Методичне забезпечення.

- Навчально-тематичний план.

- Зміст програми.

Пояснювальна записка

У наш час розуміння відсотків і уміння виконувати відсоткові розрахунки потрібні кожній людині: прикладне значення цієї теми дуже велике і пов’язане з багатьма сферами нашого життя, саме з фінансовою, соціологічною та іншими. Так як тема «Відсотки» пов'язує між собою багато точних і природничих наук, то вона показує учням зв’язок математики та інших наук.

Тема «Відсотки» розпорошено висвітлена в підручниках математики. Задачі на відсоткові розрахунки незначними групами розміщені в підручниках різних класів, без урахування вікових можливостей учнів. Вивчення цієї теми в основній школі є нетривалим, а учні через вікові особливості ще не можуть отримати повноцінні уявлення про відсотки, про їх роль в повсякденному житті. На наступних етапах навчання повторного звернення до цієї теми не передбачається. У багатьох шкільних підручниках можна зустріти завдання на відсотки, проте в них відсутнє компактне і чітке викладання теоретичних відомостей.

Текстові завдання на відсоткові розрахунки включені в зовнішнє незалежне оцінювання, в ДПА за курс неповної середньої школи та в завдання підсумкових робіт за курс середньої школи.

Проте завдання на відсотки досить часто викликають утруднення у школярів. Тому дана програма створена для об'єднання отриманих знань учнів в цілісну систему і для демонстрування учням застосування математичного апарату до розв'язання повсякденних завдань кожної людини. Матеріал даного курсу допоможе закріпити вміння пов'язані з відсотковими обчисленнями і сформувати стійкий інтерес до навчання.

Використання її можливе в 11 класі, як повторення матеріалу перед ЗНО, або ж як факультативний курс, чи для підготовки учнів до олімпіад тощо. Деякі заняття з цієї програми можна використовувати з учнями починаючи з 8 класів для формування практичних навичок застосування отриманих знань з теми «Відсотки» в житті.

Дана навчальну програма курсу «Відсотки» складена у відповідності з навчальною програмою математики (5-6 класи) і алгебри та відповідно до вимог державного освітнього стандарту основної загальної освіти з математики.

Цей курс передбачає чіткий виклад теоретичних питань, розв’язування типових завдань, завдань з практичним змістом, а саме таких завдань, які пов'язані із застосуванням відсоткових обчислень в повсякденному житті. Пропоновані завдання різні по рівню складності: від простих вправ на застосування вивчених формул до прийомів розрахунку відсотків в реальних ситуаціях (наприклад, обчислення банківських ситуації).

Пропонований курс спрямований на те, щоб надати учням додаткові знання по відсоткові обчислення для використання їх не лише в навчально-пізнавальному процесі, але і повсякденному житті – при розрахунку вигідності банківської угоди, рентабельності бізнесу, комерційної пропозиції.

У рамках курсу пропонується розв’язання завдань, пропонованих на ЗНО, ДПА та на математичних олімпіадах.

Цей курс «Відсотки» сприятиме не лише виробленню умінь і закріпленню навичок розв’язання різних завдань, пов'язаних з відсотковими розрахунками, але і формуванню інтересу учнів до математики, сприяти їх інтелектуальному розвитку.

Клас	Тема	Учень/учениця повинні
	Відсотки	формулювати означення відсотка, знаходити відсотки від числа та число за його відсотками;
	Відсоткове відношення двох чисел. Відсоткові розрахунки.	Розв’язувати три основні задачі на відсотки; записувати відсотки у вигляді звичайного і десяткового дробів; побудувати та аналізувати стовпчасті діаграми, аналізувати кругові діаграми.
В інших класах тема відсотки окремо не виділяється, а задачі на відсотки розглядаються в інших змістових лініях ШКМ.

Завдання курсу:

- повторити і систематизувати знання про відсотки;

- створити основу для розв’язання більш складних завдань, які пов’язують зміст шкільного курсу математики з життям;

- сприяти інтелектуальному розвитку учнів, формуванню логічного мислення, розвитку практичних здібностей.

Мета курсу:

- актуалізувати раніше вивчений і новий матеріал для забезпечення учням високого рівня знань по цій темі;

- сформувати уміння виконувати відсоткові розрахунки, необхідні для застосування в практичній діяльності і в завданнях з суміжних дисциплін, зокрема з «Основ економіки»;

- підготувати учнів до ДПА чи ЗНО;

- підвищити інтерес до вивчення математики.

В результаті курсу учні повинні:

- розуміти змістовний сенс терміну «відсоток» як спеціального способу вираження долі величини;

- знати широту застосування процентних обчислень в житті;

- уміти застосовувати формули «простих» і «складних» відсотків, знаходження відсотків від числа чи числа за його відсотками, формули відсоткового вмісту речовини;

Способи організації діяльності учнів на різних уроках:

- на уроках-лекціях учні вчаться конспектувати, аналізувати вивчені нові методи розв’язування завдань;

- на уроках-бесідах спільними зусиллями учителі і учнів вирішуються ключові завдання;

- на уроках-практикумах учні самостійно вирішують завдання, домагаючись тих або інших навичок, аналізують помилки і шляхи їх виправлення;

- на уроках-семінарах учні розповідають про виконану роботу, скажімо, про рішення якихось завдань з домашньої роботи, оцінюють розв’язання, оцінюють свою діяльність та діяльність інших.

 

Методичне забезпечення

Даний курс складається з теоретичної і практичної частин.

Форми організації навчання: індивідуальна, групова, колективна, взаємне навчання, самонавчання (при цьому вчитель контролює, корегує і направляє роботу учнів) Використовується: бесіда, лекція, консультація, практичне заняття, захист проекту, ділова гра.

Засоби навчання: довідкова література (наприклад з економіки), дидактичні матеріали (наприклад статистичні відомості), творчі завдання для групової роботи, мультимедійні засоби.

Технології навчання: інформаційні, модульне навчання, різнорівневі навчання, дослідницькі методи. Заняття носять проблемний характер. Передбачаються відповіді на питання в процесі дискусії, пошук інформації по суміжних галузей знань.

Кількість годин: вивчення спецкурсу розраховане на 17 години, орієнтовно 2 години в тиждень, кількість годин може змінюватись відповідно до бажань і потреб вчителя і учнів.

.

 

 

Навчально-тематичний план

№	Теми	Кількість годин
1.	Історія виникнення поняття відсотка
2.	Знаходження відсотків від числа і числа за його відсотками
3.	Завдання на суміші, сплави, концентрацію і відсотковий вміст
4.	Розв’язання завдань за допомогою рівнянь і нерівностей
5.	Завдання на відсотки в економіці
6.	Олімпіадні завдання
7.	Відсотки на ДПА та ЗНО
8.	Відсотки в нашому житті
9.	Заліковий урок

Форма контролю

Підсумкова оцінка за курс може проводитися у формі письмової контрольної роботи.

Зміст програми

Тема 1. Історія виникнення поняття відсотка (1 год.)

Заняття 1. Історія виникнення поняття відсотка

Форма проведення заняття: бесіда з використанням мультимедійних засобів (так як учні знайомі з даним матеріалом з курсу математики 5-6 класів, то дане заняття проводиться у формі бесіди для повторення і систематизації знань з даної теми).

Прийоми і методи: роз'яснення; роз`язування завдач за означенням.