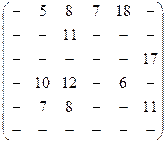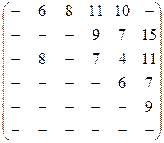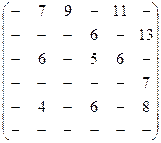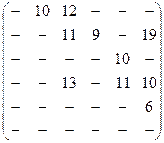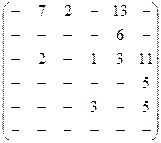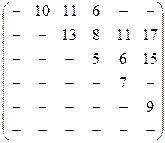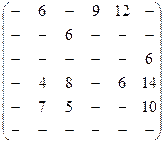Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень рекомендуемой литературы по курсу «логика» («логика и дискретная математика»)Содержание книги
Поиск на нашем сайте
1. Учебник логики. Со сборником задач: учебник/ А. Д. Гетманова. М.: КНОРУС, 2011. 2. Логика: учебник/ С.С. Гусев, Э.Ф. Караваев, Г.В. Карпов [и др.]; под. ред. А. И. Мигунова, И.Б. Микиртумова, Б. И. Федорова. М.: Проспект, 2010. 3. Логика: учебно-методическое пособие/ В. Н. Ксенофонтов. М.: Изд-во РАГС, 2010. 4. Дискретная математика.Курс лекций / И.А. Палий. М.: Эксмо, 2008. 5. Дискретная математика. Курс лекций и практических занятий/ С.Д. Шапорев. СПб.:БХВ-Петербург, 2007. 6. Эдельман С.Л. Математическая логика. М.: Высшая школа, 1975.
КОНТРОЛЬНОЕ ЗАДАНИЕ Выполняется одно контрольное задание, в котором содержится 6 задач. По выданному преподавателем номеру варианта задания с помощью таблицы вариантов, приведенной на следующей странице, определяются номера варианты входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении. Срок сдачи задания: 16 неделя (до 20 декабря). Сроки зачета задания (с учетом исправления ошибок): 17 неделя (до 27 декабря). Таблица вариантов
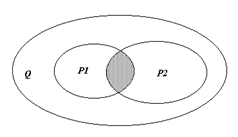
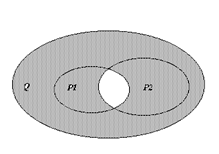
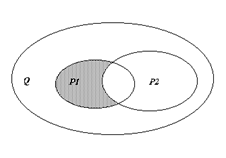
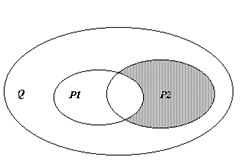
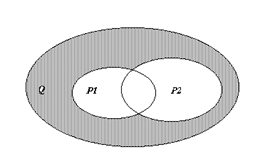
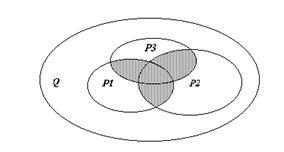
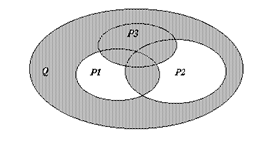
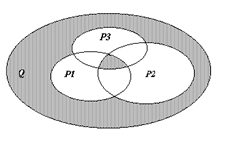
Контрольное задание Задача 1. На заданном множестве точек плоскости Q определены предикаты P 1 (x), P 2 (x), P(x). Областью истинности предиката P 1 (x) является множество Р1, областью истинности предиката P 2 (x) – множество Р2, областью истинности предиката Р(х) – множество Р, заштрихованная часть области Q. a) Используя операции над множествами, записать формулу получения множества Р. б) Используя логические операции, записать формулу предиката P(x).
Задача 2. Дано множество M= { a, b }. Предикат P(x,y), где x Î M, yÎ M, задан следующей таблицей.
Определить значение истинности высказывания (с объяснением)
Задача 3. Выписать все элементы отношений
Задача 4. Решить задачу
Задача 5. Для орграфа, представленного следующей матрицей инциденций, найти матрицу смежности, нарисовать диаграмму графа и определить будет ли он связным, сильно связным или несвязным.
Для орграфа, представленного следующей матрицей смежности, найти матрицу инциденций, нарисовать диаграмму графа и определить будет ли он связным, сильно связным или несвязным.
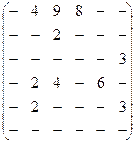
Задача 5. По заданной матрице расстояний графа G найти величину минимального пути и сам путь от вершины s = х1 до вершины t=х6, а затем величину максимального пути и сам путь между теми же вершинами.
ВОПРОСЫ К ЗАЧЕТУ ПО КУРСУ «ЛОГИКА» («ЛОГИКА И ДИСКРЕТНАЯ МАТЕМАТИКА») 1. Логика как наука, ее предмет, структура, значение. 2. Виды логик. 3. Понятие как форма мышления. 4. Понятие и представление. Понятие и термин. Определение и структура понятия. 5. Содержание и объем понятия. 6. Виды понятий. 7. Классификация понятий. 8. Суждение. Виды суждений. 9. Объединенная классификация суждений по качеству и количеству. 10. Виды суждений, не рассматриваемых в классической логике. 11. Комплексный анализ простого категорического суждения. 12. Умозаключения. 13. Дедуктивные умозаключения. 14. Силлогистика. Основные понятия. 15. Индуктивные умозаключения и их виды. 16. Логические основы теории аргументации. 17. Виды и правила доказательства и опровержения. 18. Основные законы логики (тождества, противоречия, исключенного третьего, достаточного основания). 19. Суждения и высказывания как формы мышления. 20. Основные операции над высказываниями. Таблицы истинности. 21. Эквивалентные высказывания и логические законы. 22. Одноместные предикаты: основные понятия. 23. Одноместные предикаты: использование кванторов общности и существования. 24. Двухместные предикаты: основные понятия. 25. Двухместные предикаты: использование кванторов общности и существования. 26. Логические законы, формулирующиеся с использованием кванторов. 27. Множества и классы понятий, основные операции над ними. Круги Эйлера. 28. Прямое (декартово) произведение множеств. Комбинаторные структуры. 29. Понятие отношения. Обратное отношение. Графическое представление бинарных отношений. 30. Отношения эквивалентности. Свойства отношений. Разбиения множеств на классы. 31. Отношения порядка. Свойства отношений. 32. Отображения и их основные свойства. Виды отображений. 33. Комбинаторные структуры (размещения, перестановки, сочетания). 34. Перестановки с учетом повторений. 35. Сочетания с учетом повторений. 36. Бином Ньютона. 37. Биномиальные коэффициенты. Свойства биномиальных коэффициентов. 38. Треугольник Паскаля. 39. Ориентированные графы. Диаграмма графа. Матрицы смежности, инциденций и достижимости. 40. Изоморфизм графов. 41. Маршруты, цепи, циклы. 42. Операции над графами. 43. Деревья (ориентированные, сбалансированные, бинарные, остовные). 44. Разрезы. 45. Потоковые модели. 46. Социометрические модели.
ПРИЛОЖЕНИЕ.
Задание по логике
Слушателя группы О-911 Иванова Петра Фомича Вариант 15
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.107 (0.007 с.) |



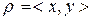 и
и 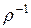 . Исследовать свойства отношения
. Исследовать свойства отношения  и представить его в виде ориентированного графа и координатной диаграммы.
и представить его в виде ориентированного графа и координатной диаграммы.
 -1 0 -1 0 -1 0 0
0 -1 0 0 0 0 -1
1 1 0 0 0 0 0
0 0 1 -1 0 0 0
0 0 0 0 0 -1 1
0 0 0 1 1 1 0
-1 0 -1 0 -1 0 0
0 -1 0 0 0 0 -1
1 1 0 0 0 0 0
0 0 1 -1 0 0 0
0 0 0 0 0 -1 1
0 0 0 1 1 1 0



 0 1 1 1 1
1 0 1 0 0
1 1 0 1 0
1 0 1 0 0
1 0 0 0 0
0 1 1 1 1
1 0 1 0 0
1 1 0 1 0
1 0 1 0 0
1 0 0 0 0
 0 1 0 1 0
1 0 1 1 0
0 1 0 0 1
1 1 0 0 0
0 0 1 0 0
0 1 0 1 0
1 0 1 1 0
0 1 0 0 1
1 1 0 0 0
0 0 1 0 0
 0 1 1 0 0
1 0 0 0 0
1 0 0 1 1
0 0 1 0 0
0 0 1 0 0
0 1 1 0 0
1 0 0 0 0
1 0 0 1 1
0 0 1 0 0
0 0 1 0 0

 0 1 1 1 1
1 0 0 1 1
1 0 0 0 1
1 1 0 0 1
1 1 1 1 0
0 1 1 1 1
1 0 0 1 1
1 0 0 0 1
1 1 0 0 1
1 1 1 1 0

 0 1 1 1 0
1 0 0 0 1
1 0 0 1 0
1 0 1 0 1
0 1 0 1 0
0 1 1 1 0
1 0 0 0 1
1 0 0 1 0
1 0 1 0 1
0 1 0 1 0