
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По физике 2-го уровня сложностиСодержание книги
Поиск на нашем сайте
Утверждено Редакционно – издательским советом университета в качестве практического пособия
Курск 2007 УДК 531/534 ББК В21 Л 68 Рецензенты: Доктор физико-математических наук, зав. кафедрой «Теоретическая и экспериментальная физика» Курского государственного технического университета, профессор А.А. Родионов Доктор физико-математических наук, зав. кафедрой «Общая физика» Курского государственного университета, профессор Ю.А. Неручев Кандидат технических наук, зав. кафедрой «Физика» Курской сельскохозяйственной академии им. профессора И.И. Иванова Д.И. Якиревич Лобова, О.В. Сборник тестовых контрольных заданий (модулей) по физике 2-го уровня сложности:практическое пособие. [Текст]: /О.В. Лобова, В.М. Полунин, Г.Т. Сычев; Курск. гос. техн. ун - т. Курск, 2007. 146 с. Ил. 225, прилож. 4 Библиограф.: 145 с.
Практическое пособие составлено в соответствии с требованиями Государственного образовательного стандарта, Примерной программы дисциплины «Физика» и рабочей программы по физике для студентов инженерно-технических специальностей КурскГТУ. Излагаются тестовые контрольные задания (модули) по механике и молекулярной физике II уровня сложности для выполнения индивидуальных заданий. Содержит варианты заданий, основные формулы, необходимые приложения и таблицы. Предназначено для индивидуальной самостоятельной работы по физике студентов инженерно-технических специальностей всех формы обучения.
УДК 531/534 ББК В21 Л 68 Ó Курский государственный технический университет, 2007 Ó Лобова О.В., Полунин В.М., Сычев Г.Т., 2007 Оглавление
Предисловие…………………………………………………...4
I. Физические основы механики. Модуль №1..........6
II. Физические основы механики. Модуль №2.…..48
III. Основы молекулярной физики и термодинамики. Модуль №3..... ………………………...85
Заключение.…………………………………………………134 Приложение 1..………………………………………………135
Приложение 2...…………………………………………..….136
Приложение 3……………………………....………..............140
Приложение 4………………………………………………..141
Библиографический список………………………….145
Предисловие
Письменное тестовое задание по физике позволяет выяснить знания студентов инженерно-технических специальностей основных понятий, законов и формул, выявить индивидуальное умение каждого студента применять полученные теоретические знания к решению практических задач, уровень их физической подготовки, глубину и прочность навыков, необходимых инженерам в процессе их дальнейшей деятельности. В данной работе представлены контрольные задания (модули) 2-го уровня сложности, которые предназначены для студентов, получивших глубокие знания на предшествующем этапе обучения по физике, наиболее одаренных студентов. Однако это не означает, что вышеуказанные студенты не могут выполняять контрольные задания (модули) 1-го уровня сложности. Студенту предлагается выполнить письменное задание (модуль), состоящей из тестовых задач. Каждый модуль содержит: · Модуль №1 – 8 задач по разделу «Физические основы механики (кинематика и динамика, колебания и волновые процессы» ". · Модуль №2 – 7 задач по разделу «Физические основы механики (энергия, работа, мощность; законы сохранения в механике; поле тяготения; движение в поле центральных сил)». · Модуль №3 – 10 задач по разделу "Основы молекулярной физики и термодинамики (конденсированное состояние; кинематика и динамика жидкостей; основные представлениямолекулярно–кинетической теории;статистический метод исследования; основы термодинамики; реальные газы; фазовые равновесия и превращения; кинетические явления) ". Задача считается решенной правильно, если полученный студентом в ходе ее решения ответ полностью соответствует одному из приведенных в задаче. За каждую правильно решенную задачу студент получает определенное число баллов, которое определяется рейтинговой накопительной системой. Тестовое задание (модуль) выполняется студентами в процессе самостоятельной работы в семестре. Использование справочной литературы допускается. Выполнненный и зачтенный модуль является промежуточной аттестацией самостоятельной работы студента в семестре. Предполагается, что, работая с данным пособием, студенты будут пользоваться не только им, но и задачниками (другими книгами, справочниками по физике), в которых они найдут необходимый теоретический и справочный материалы. Авторы, при подборе задач руководствовались следующим принципом: «Задачи должны быть такими, чтобы при их решении основное внимание уделялось физической стороне вопроса». Большинство задач для самостоятельного решения, приведенных в данном пособии, взято из задачников. Многие задачи переработаны. Часть задач составлена авторами этой книги. В приложении приведены основные формулы и законы, некоторые правила приближенных вычислений и справочные таблицы, а в конце – библиографический список рекомендательной литературы. Изложение материала в данной работе предусматривает знание студентами математики в объеме школьной программы. Кроме того, предполагается, что студенты уже изучили или изучают параллельно читаемому курсу соответствующий «вузовский» материал (дифференциальное и интегральное исчисление, анализ функций, дифференциальные уравнения, векторную алгебру, ряды). Обозначения единиц измерения физических величин даны через основные и производные единицы системы СИ. Практическое пособие может быть использовано преподавателями, имеющими недостаточный опыт работы в вузе. Авторы будут благодарны всем, кто внимательно просмотрит данную книгу и выскажет определенные замечания по существу. Кроме того, они постараются учесть все рациональные замечания со стороны коллег – физиков, студентов, и внести соответствующие исправления и дополнения.
I. Физические основы механики. Модуль №1 Кинематика и динамика. Колебания и волновые процессы Вариант № 1 1. Тело, двигаясь с постоянным ускорением, проходит последовательно два одинаковых отрезка пути S по 10 м каждый. Найти ускорение в начале первого отрезка, если первый отрезок пройден телом за время t1=1,06 с, а второй за t2=2,2 с.
Ответ: а) а=3 м/с2; б) a=2 м/с2; в) a=1 м/с2; г) a=0; д) а=-3 м/с2.
2. Две гири массами m1=1 кг и m2=2 кг соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса M=1 кг. Найти ускорение, с которым движутся гири. Блок считать однородным диском. Трением пренебречь.
Ответ: а) а=3,8 м/с2; б) а=2,8 м/с2; в) а=4,8 м/с2; г) а=1,8 м/с2; д) а=0,8 м/с2.
Ответ: а) tА/tВ=2,6; б) tА/tВ=2,4; в) tА/tВ=2,2; г) tА/tВ=2;
4. Из отверстия шланга, прикрытого пальцем, бьют две струи под углом α=450 и β=600 к горизонту с одинаковой скоростью v=5 м/с. На каком расстоянии по горизонтали струи пересекутся (рис. 3)? Ответ: а) ℓ=5,24 м; б) ℓ=2,24 м; в) ℓ=3,24 м; г) ℓ=4,24 м; д) ℓ=1,24 м.
Ответ: а) a3=14,0 м/с2; б) a3=15,0 м/с2; в) a3=16,0 м/с2; г) a3=17,0 м/с2; д) a3=18,0 м/с2.
6. Точка соверает гармоническое колебание. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти амплитуду этого колебания. Ответ: а) А=0,24 м; б) А=0,024 м; в) А=0,34 м; г) А=0,034 м; д) А=0,014 м.
Ответ: а) e=22%; б) e=1,2%; в) e=2,2%; г) e=12%; д) e=0,2%.
8. Однородная палочка подвешена за оба конца на двух одинаковых нитях длиной ℓ=1 м. В состоянии равновесия обе нити параллельны. Найти период Т малых колебаний, возникающих после некоторого поворота палочки вокруг вертикальной оси, проходящей через середину палочки. Ответ: а) Т=1,20 с; б) Т=1,16 с; в) Т=1,12 с; г) Т=1,08 с; д) Т=1,04 с. Вариант № 2 1. Зависимость координаты прямолинейно движущегося тела от времени выражается уравнением x=0,25t4-9t5. Найти экстремальное значение скорости тела. Ответ: а) vmax=0,11×10-6 м/с; б) vmax=1,1 м/с; в) vmax=11×10-6 м/с; г) vmax=10,1×10-6 м/с; д) vmax=2,1×10-6 м/с.
Ответ: а) Т1=2 Н; б) Т1=12 Н; в) Т1=3 Н; г) Т1=0,2 Н; д) Т1=1 Н.
Ответ: а) l=10 м; б) l=14 м; в) l=18 м; г) l=22 м; д) l=26 м.
Ответ: а) v=0,77 м/с; б) v=1,77 м/с; в) v=2,77 м/с; г) v=3,77 м/с; д) v=4,77 м/с.
Ответ: а) а1 =1,0 м/с2; б) а1 =1,2 м/с2; в) а1 =1,4 м/с2; г) а1 =1,6 м/с2; д) а1 =1,8 м/с2.
6. Точка совершает гармоническое колебание. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти период этого колебания.
г) Т=4,1 с; д) Т=5,1 с.
7. Определить период колебания массы m=121 г ртути, находящейся в U - образной трубке (рис. 5). Площадь сечения канала трубки S=0,3 см2. Ответ: а) Т=0,97 с; б) Т=0,77 с; в) Т=0,57 с; г) Т=0,37 с; д) Т=0,17 с.
Ответ: а) Т=2,6 с; б) Т=2,4 с; в) Т=2,2 с; г) Т=2,0 с; д) Т=1,6 с. Вариант № 3 1. Одновременно из одного пункт выезжают две автомашины, которые движутся в одном направлении неравномерно. Зависимость пройденного автомобилями пути от времени выражается уравнениями S1=t-0,2t2 и S2=2t+t2-0,6t3. Найти относительную скорость автомашин в момент времени t=5 с.
д) v12=42 м/с.
2. Две гири массами m1=1 кг и m2=2 кг соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса M=1 кг. Найти натяжение нити, к которой подвешена вторая гиря. Блок считать однородным диском. Трением пренебречь. Ответ: а) Т2=1,4 Н; б) Т2=0,4 Н; в) Т2=14 Н; г) Т2=4 Н; д) Т2=24 Н. 3. Две частицы движутся с ускорением g в однородном поле тяжести. В начальный момент частицы находились в одной точке и имели скорости v01=3,0 м/с и v02=4,0 м/с, направленные горизонтально и в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными (α=900) (рис. 2).
4. В момент времени, когда модуль скорости v=106 м/с, ускорение частицы а=104 м/с2 и направлено под углом 300 к вектору скорости. На сколько увеличится модуль скорости за время Δt=10-2 с? Ответ: а) Δv=0,87∙102 м/с; б) Δv=0,77∙102 м/с; в) Δv=0,67∙102 м/с; г) Δv=0,57∙102 м/с; д) Δv=0,47∙102 м/с.
Ответ: а) а= -0,5 м/с2; б) а= -0,4 м/с2; в) а= -0,3 м/с2; г) а= -0,2 м/с2; д) а= -0,1 м/с2.
6. Точка одновременно совершает два гармонических колебания, происходящих по одной и той же прямой. Амплитуды колебаний одинаковы, периоды равны 0,1 с и 0,102 с. Найти период изменения амплитуды результирующего колебания (период биений). Ответ: а) Тб=1,1 с; б) Тб=2,1 с; в) Тб=3,1 с; г) Тб=4,1 с; д) Тб=5,1 с.
7. Предположим, что по одному из диаметров Земли просверлен канал. Принимая Землю за однородный шар, найти время t движения тела от поверхности Земли до ее центра. Плотность Земли принять равной r=5,5×103 кг/м3 Ответ: а) t=23 мин; б) t=21 мин; в) t=19 мин; г) t=17 мин; д) t=15 мин.
8. Сплошной шар радиуса r=0,2 м с моментом инерции I (относительно геометрической оси) и массой m катается без скольжения по внутренней поверхности цилиндра радиуса R=1 м, совершая малые колебания около положения равновесия (рис. 4). Найти период колебаний.
г) Т=2,12 с; д) Т=2,02 с.
Вариант № 4 1. Винт аэросаней вращается с частотой n =6 с-1. Скорость поступательного движения саней v=54 км/ч. С какой скоростью движется один из концов винта, если радиус винта R=1 м? Ответ: а) v=20,6 м/с; б) v=30,6 м/с; в) v=40,6 м/с; г) v=50,6 м/с; д) v=60,6 м/с.
Ответ: а) а=1,53 м/с2; б) а=2,53 м/с2; в) а=3,53 м/с2; г) а=2 м/с2; д) а=0,53 м/с2.
3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с2. Через 2,0 с после начала подъема с потолка кабины стал падать болт. Найти время свободного падения болта. Ответ: а) t=0,5 с; б) t=0,7 с; в) t=0,9 с; г) t=1,1 с; д) t=1,3 с.
Ответ: а) Δφ=1∙10-5 рад; б) Δφ=2∙10-5 рад; в) Δφ=3∙10-5 рад; г) Δφ=4∙10-5 рад; д) Δφ=5∙10-5 рад.
5. На рисунке 2 изображен прибор для пояснения зависимости центробежной силы от массы и расстояния от оси вращения. Шары А и В имеют диаметры 3 см и 2 см. Соединяющий шары шнур имеет длину l=10,5 см. На каком расстоянии x от оси ОО должен быть помещен центр шара А, чтобы при вращающемся приборе шары удерживались на неизменном расстоянии от оси? Шары сделаны из одного и того же материала. Объемом канала, просверленного внутри шаров, можно пренебречь. Ответ: а) x =1,6 см; б) x =1,8 см; в) x =2,0 см; г) x =2,2 см; д) x =2,4 см.
6. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями Ответ: а) y=1-x2; б) y=1+3x2; в) y=1-3x2; г) y=1+2x2; д) y=1-2x2.
7. Каков логарифмический декремент затухания маятника длиной 0,8 м, если его начальная амплитуда 50, а через время 5 мин амплитуда равна 0,50? Ответ: а) l=0,014; б) l=0,024; в) l=0,14; г) l=0,24; д) l=0,034.
Ответ: а) Т=1,03 с; б) Т=0,93 с; в) Т=0,83 с; г) Т=0,73 с; д) Т=0,63 с. Вариант № 5 1. На столе лежит доска массой М=1 кг, а на доске – груз массой m=2 кг. Какую силу нужно приложить к доске, чтобы доска выскользнула из – под груза? Коэффициент трения между грузом и доской m1=0,25, а между доской и столом m2=0,5. Ответ: а) F ≥2,21 Н; б) F ≥22,1 Н; в) F ≥12,1 Н; г) F ≥32,1 Н; д) F ≥15,1 Н.
2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m1=m2=1 кг соединены нитью, перекинутой через блок (рис. 1). Коэффициент трения гири, лежащей на столе, о стол равен 0,1. Найти натяжение нити, к которой прикреплена гиря, лежащая на столе.
3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с2. Через 2,0 с после начала подъема с потолка кабины стал падать болт. Найти перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта. Ответ: а) Dr=0,7 м; S=1,3 м; б) Dr=0,5 м; S=1,2 м; в) Dr=0,6 м; S=1,1 м; г) Dr=0,8 м; S=1 м; д) Dr=0,4 м; S=1,4 м.
4. В момент времени, когда модуль скорости v=106 м/с, ускорение частицы а=104 м/с2 и направлено под углом 300 к вектору скорости. Какова угловая скорость вращения вектора скорости в момент времени t=10-2 c? Ответ: а) ω=6∙10-3 рад/с; б) ω=5∙10-3 рад/с; в) ω=4∙10-3 рад/с; г) ω=3∙10-3 рад/с; д) ω=2∙10-3 рад/с.
5. Грузик привязан к нити, другой конец которой прикреплен к потолку. Вследствие толчка грузик движется по окружности, плоскость которой отстоит от потолка на h=1,5 м. Какова частота оборотов грузика? Ответ: а) n=0,1 с-1; б) n=0,8 с-1; в) n=0,2 с-1; г) n=0,6 с-1; д) n=0,4 с-1.
6. Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражается уравнениями x=0,5sinwt, y=coswt. Найти уравнение траектории точки. Ответ: а) y2+16x2=4; б) y2-16x2=4; в) y2+12x2=4; г) y2-12x2=4; д) y2+10x2=4.
7. Какова общая сумма путей, пройденных взад и вперед колеблющейся точкой до полного затухания колебаний, если амплитуда первого колебания равна 1 мм, а логарифмический декремент затухания равен 0,002? Ответ: а) S=2 м; б) S=3 м; в) S=5 м; г) S=6 м; д) S=7 м.
Ответ: а) ℓ=0,15 м; б) ℓ=0,25 м; в) ℓ=0,35 м; г) ℓ=0,015 м; д) ℓ=0,025 м. Вариант № 6 1. На вал радиусом 1 см намотана нить, к концу которой привязана гиря. Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти полное ускорение точки, лежащей на поверхности вала, в конечный момент движения. Ответ: а) a=1,6 м/с2; б) a=2,6 м/с2; в) a=3,6 м/с2; г) a=4,6 м/с2; д) a=5,6 м/с2.
Ответ: а) Т2=1,3 Н; б) Т2=2,3 Н; в) Т2=3,3 Н; г) Т2=6,3 Н; д) Т2=8,3 Н.
Ответ: а) Dt=10 с; б) Dt=12 с; в) Dt=14 с; г) Dt=16 с; д) Dt=18 с.
4. Тело движется по окружности радиуса r=2 м со скоростью, которая линейно увеличивается во времени: Ответ: а) а =6,25 м/с2; б) а =7,25 м/с2; в) а =8,25 м/с2; г) а =5,25 м/с2; д) а =4,25 м/с2.
Ответ: а) а =0,2 м/с2; б) а =0,3 м/с2; в) а =0,1 м/с2; г) а =0,5 м/с2; д) а =0,1 м/с2.
6. Складываются два колебания одинакового направления и одинакового периода x1=sinpt и x2=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Определить амплитуду А результирующего колебания. Ответ: а) А=1,2 см; б) А=1,4 см; в) А=1,6 см; г) А=1,8 см; д) А=2,0 см.
7. Амплитуды скорости вынужденных колебаний при частотах вынуждающей силы n1=200 Гц и n2=300 Гц равны между собой. Принимая, что амплитуда вынуждающей силы в обоих случаях одна и та же, найти частоту, соответствующую резонансу скорости. Ответ: а) n=245 Гц; б) n=345 Гц; в) n=145 Гц; г) n=445 Гц; д) n=45 Гц.
Ответ: а) ТА=0,18 с; б) ТА=0,13 с; в) ТА=0,23 с; г) ТА=0,33 с; д) ТА=0,28 с.
Вариант № 7 1. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара мяча о стенку на 1 м меньше высоты, с которой брошен мяч. Под каким углом мяч подлетает к поверхности стенки? Сопротивление воздуха не учитывать. Ответ: а) a=210; б) a=310; в) a=110; г) a=150; д) a=410.
Ответ: а) a =16,40; б) a =26,40; в) a =36,40; г) a =46,40; д) a =56,40.
Ответ: а) m=0,14; б) m=0,16; в) m=0,18; г) m=0,20; д) m=0,22.
Ответ: а) а=5,8 м/с2; б) а=6,8 м/с2; в) а=7,8 м/с2; г) а=8,8 м/с2; д) а=9,8 м/с2.
Ответ: а) v=8 м/с; б) v=10 м/с; в) v=12 м/с; г) v=14 м/с; д) v=7 м/с.
6. Складываются два колебания одинакового направления и одинакового периода x1=sinpt и x2=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Определить начальную фазу jо результирующего колебания. Ответ: а) j0=p/2; б) j0=p/3; в) j0=p/4; г) j0=p; д) j0=p/6.
7. Амплитуды смещений вынужденных колебаний при частотах вынуждающей силы n1=200 Гц и n2=300 Гц, равны между собой. Найти частоту, соответствующую резонансу смещений. Ответ: а) n=355 Гц; б) n=255 Гц; в) n=155 Гц; г) n=55 Гц; д) n=555 Гц.
Ответ: а) ТВ=0,53 с; б) ТВ=0,43 с; в) ТВ=0,33 с; г) ТВ=0,23 с; д) ТВ=0,13 с.
1. Тело брошено со скоростью 20 м/с вверх под углом 30о к горизонту (рис. 1). Найти радиус кривизны траектории в точке, в которой окажется тело через одну секунду после начала движения. Ответ: а) R=31 м; б) R=21 м; в) R=11 м; г) R=1,1 м; д) R=3,1 м.
Ответ: а) v2=0,5 м/с; б) v2=1,5 м/с; в) v2=3,5 м/с; г) v2=4,5 м/с;
3. Небольшое тело А начинает скользить с вершины клина, основание которого а=2,10 м. Коэффициент трения между телом и поверхностью клина m=0,14 (рис. 3). При каком значении угла a время соскальзывания будет наименьшим? Ответ: а) a=690; б) a=590; в) a=490; г) a=390; д) a=290.
4. Материальная точка начинает двигаться по окружности радиусом r=12,5 см с постоянным тангенциальным ускорением aτ=0,5 м/с2. Определить момент времени, при котором вектор ускорения Ответ: а) t=1 с; б) t=2 с; в) t=3 с; г) t=4 с; д) t=5 с.
5. Вертикальный столб высотой h=5 м подпиливается у основания и падает на Землю. Какая точка столба будет в любой момент падения столба иметь ту же скорость, какую имело бы тело, падая с той же высоты, как и данная точка (рис. 4)? Ответ: а) h1=4/3 h; б) h1=1/3 h; в); г) h1=2/3 h; д) h1=5/3 h.
6. Складываются два колебания одинакового направления и одинакового периода x1=sinpt и x2=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Получить уравнение результирующего колебания. Ответ: а) x=1,4sinπ(t-1/2); б) x=1,4sinπ(t+1/2); в) x=1,4sinπ(t-1/4); г) x=1,4sinπ(t+1/4); д) x=1,4sinπ(t+1/3).
7. Амплитуда смещения вынужденных колебаний при очень малой частоте равна x0=2 мм, а при резонансе равна X0=16 мм. Предполагая, что декремент затухания меньше единицы, определить его. Ответ: а) D=0,25; б) D=0,3; в) D=0,4; г) D=0,2; д) D=0,1.
Ответ: а) ТА/ТВ=0,69; б) ТА/ТВ=0,59; в) ТА/ТВ=0,49; г) ТА/ТВ=0,39; д) ТА/ТВ=0,29. Вариант № 9
Ответ: а) h=6,35 м; б) h=7,35 м; в) h=8,35 м; г) h=9,35 м; д) h=10,35 м.
Ответ: а) t7=0,5 с; б) t7=0,6 с; в) t7=0,7 с; г) t7=0,8 с; д) t7=0,9 с.
3. Небольшое тело А (рис. 2) начинает скользить с вершины клина, основание которого а=2,10 м. Коэффициент трения между телом и поверхностью клина m=0,14. Чему равно наименьшее время соскальзывания при угле a=490? Ответ: а) tmin=1,6 с; б) tmin=1,4 с; в) tmin=1,2 с; г) tmin=1,0 с; д) tmin=0,8 с.
4. Материальная точка начинает двигаться по окружности радиусом r=12,5 см с постоянным тангенциальным ускорением равным aτ=0,5 м/с2. Определить путь, пройденный движущейся точкой за промежуток времени, по прошествии которого вектор ускорения Ответ: а) S=6,25 см; б) S=5,25 см; в) S=7,25 см; г) S=4,25 см; д) S=8,25 см.
Ответ: а) F=5,85 Н; б) F=4,85 Н; в) F=3,85 Н; г) F=2,85 Н; д) F=1,85 Н.
6. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых следующими уравнениями x=sin Ответ: а) y=1-x2; б) y=1+3x2; в) y=1-3x2; г) y=1+2x2; д) y=1-2x2.
7. Точка совершает гармонические колебания вдоль некоторой прямой с периодом T=0,60 с и амплитудой x0=10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь, равный x0/2: а) из крайнего положения; б) из положения равновесия. Ответ: а) <v1>=1,5 м/с; <v2>=1,5 м/с; б) <v1>=2,5 м/с; <v2>=2,0 м/с; в) <v1>=0,3 м/с; <v2>=1,5 м/с; г) <v1>=0,5 м/с; <v2>=1,0 м/с; д) <v1>=2,0 м/с; <v2>=1,5 м/с.
Ответ: а) Т»1,89 с; б) Т»1,79 с; в) Т»1,59 с; г) Т»2,29 с; д) Т»1,29 с. Вариант № 10
Ответ: а) a=0,19 м/с2; б) a=0,9 м/с2; в) a=0,29 м/с2; г) a=0,39 м/с2; д) a=0,49 м/с2.
Ответ: а) a=-0,45 м/с2; б) a=-0,35 м/с2; в) a=-0,25 м/с2; г) a=-0,15 м/с2; д) a=-0,05 м/с2.
3. В установке (рис. 2) шарик 1 имеет массу в n=1,8 раза больше массы стержня 2. Длина последнего l=100 см. Шарик установили на одном уровне с нижним концом стержня и отпустили. Через сколько времени он поравняется с верхним концом стержня? Массой блоков и нитей, а также трением пренебречь. Ответ: а) t=1,6 с; б) t=1,5 с; в) t=1,0 с; г) t=1,2 с; д) t=1,4 с.
Ответ: а) w=15,4 рад/с; б) w=13,4 рад/с; в) w=11,4 рад/с; г) w=
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.016 с.) |


 3. От бакена, который находится на середине широкой реки, отошли две лодки – А и В (рис. 2). Обе лодки движутся по взаимно перпендикулярным прямым: лодка А – вдоль реки, а лодка В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок tА/tВ, если скорость каждой лодки относительно воды в n=1,2 раза больше скорости течения реки.
3. От бакена, который находится на середине широкой реки, отошли две лодки – А и В (рис. 2). Обе лодки движутся по взаимно перпендикулярным прямым: лодка А – вдоль реки, а лодка В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок tА/tВ, если скорость каждой лодки относительно воды в n=1,2 раза больше скорости течения реки. д) tА/tВ=1,8.
д) tА/tВ=1,8.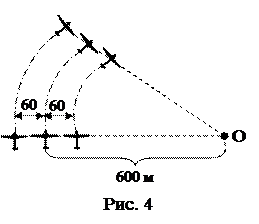 5. Три самолета выполняют разворот, двигаясь на расстоянии 60 м друг от друга (рис. 4). Средний самолет летит со скоростью 360 км/ч, двигаясь по дуге окружности радиусом R=600 м. Определить ускорение третьего самолета.
5. Три самолета выполняют разворот, двигаясь на расстоянии 60 м друг от друга (рис. 4). Средний самолет летит со скоростью 360 км/ч, двигаясь по дуге окружности радиусом R=600 м. Определить ускорение третьего самолета. 7. Шар, радиус которого 5 см, подвешен на нити длиной 10 см (рис. 5). Определить погрешность, которую мы делаем, приняв его за математический маятник с длиной 15 см.
7. Шар, радиус которого 5 см, подвешен на нити длиной 10 см (рис. 5). Определить погрешность, которую мы делаем, приняв его за математический маятник с длиной 15 см. 2. Две гири массой m1=1 кг и m2=2 кг каждая соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса М=1 кг. Найти натяжение нити, к которой подвешена первая гиря. Блок считать однородным диском. Трением пренебречь.
2. Две гири массой m1=1 кг и m2=2 кг каждая соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса М=1 кг. Найти натяжение нити, к которой подвешена первая гиря. Блок считать однородным диском. Трением пренебречь. 3. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом j=600 к горизонту (рис. 2). Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с.
3. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом j=600 к горизонту (рис. 2). Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с. 4. По внутренней поверхности гладкого вертикального цилиндра радиуса R=0,1 м под углом α=300 к вертикали пускают шарик (рис. 3). Какую начальную скорость ему надо сообщить, чтобы он вернулся в исходную точку, сделав два оборота?
4. По внутренней поверхности гладкого вертикального цилиндра радиуса R=0,1 м под углом α=300 к вертикали пускают шарик (рис. 3). Какую начальную скорость ему надо сообщить, чтобы он вернулся в исходную точку, сделав два оборота? 5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 4), и за 2 с проходит 120 см. С какими ускорением движется верхняя точка шарика?
5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 4), и за 2 с проходит 120 см. С какими ускорением движется верхняя точка шарика? Ответ: а) Т=1,1 с; б) Т=2,1 с; в) Т=3,1 с;
Ответ: а) Т=1,1 с; б) Т=2,1 с; в) Т=3,1 с; 8. Сплошной цилиндр радиуса r=0,2 м с моментом инерции I (относительно геометрической оси) и массой m катается без скольжения по внутренней поверхности цилиндра радиуса R=1 м, совершая малые колебания около положения равновесия (рис. 6). Найти период колебаний.
8. Сплошной цилиндр радиуса r=0,2 м с моментом инерции I (относительно геометрической оси) и массой m катается без скольжения по внутренней поверхности цилиндра радиуса R=1 м, совершая малые колебания около положения равновесия (рис. 6). Найти период колебаний. Ответ: а) v12=2 м/с; б) v12=1,2 м/с; в) v12=22 м/с; г) v12=32 м/с;
Ответ: а) v12=2 м/с; б) v12=1,2 м/с; в) v12=22 м/с; г) v12=32 м/с;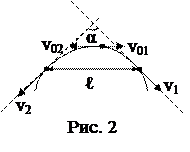 Ответ: а) l=1,5 м; б) l=2 м; в) l=2,5 м; г) l=3 м; д) l=3,5 м.
Ответ: а) l=1,5 м; б) l=2 м; в) l=2,5 м; г) l=3 м; д) l=3,5 м. 5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 3), и за 2 с проходит 120 см. С какими ускорением движется нижняя точка шарика?
5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 3), и за 2 с проходит 120 см. С какими ускорением движется нижняя точка шарика? Ответ: а) Т=2,42 с; б) Т=2,32 с; в) Т=2,22 с;
Ответ: а) Т=2,42 с; б) Т=2,32 с; в) Т=2,22 с; 2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m1=m2=1 кг соединены нитью, перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 1). Найти ускорение, с которым движутся гири.
2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m1=m2=1 кг соединены нитью, перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 1). Найти ускорение, с которым движутся гири. 4. В момент времени, когда модуль скорости v=106 м/с, ускорение частицы а=104 м/с2 и направлено под углом 300 к вектору скорости. На какой угол изменится направление скорости за время Δt=10-2 с?
4. В момент времени, когда модуль скорости v=106 м/с, ускорение частицы а=104 м/с2 и направлено под углом 300 к вектору скорости. На какой угол изменится направление скорости за время Δt=10-2 с? , y=cospt. Найти уравнение траектории точки.
, y=cospt. Найти уравнение траектории точки.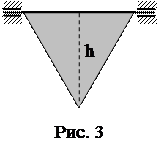 8. Достаточно тонкая пластинка из однородного материала имеет форму равностороннего треугольника высоты h=0,2 м (рис. 3). Она может вращаться вокруг горизонтальной оси, совпадающей с одной из сторон пластинки. Найти период малых колебаний такого физического маятника.
8. Достаточно тонкая пластинка из однородного материала имеет форму равностороннего треугольника высоты h=0,2 м (рис. 3). Она может вращаться вокруг горизонтальной оси, совпадающей с одной из сторон пластинки. Найти период малых колебаний такого физического маятника.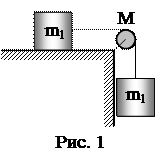 Ответ: а) Т1=0,5 Н; б) Т1=1,5 Н; в) Т1=2,5 Н; г) Т1=4,5 Н; д) Т1=3,5 Н.
Ответ: а) Т1=0,5 Н; б) Т1=1,5 Н; в) Т1=2,5 Н; г) Т1=4,5 Н; д) Т1=3,5 Н. 8. Сплошной однородный диск с радиусом r=0,1 м колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска (рис. 2). Какой длины ℓ должен быть математический маятник, имеющий тот же период колебаний, что и диск?
8. Сплошной однородный диск с радиусом r=0,1 м колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска (рис. 2). Какой длины ℓ должен быть математический маятник, имеющий тот же период колебаний, что и диск? 2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m1=m2=1 кг соединены нитью, перекинутой через блок (рис. 1). Коэффициент трения одной из гирь о стол равен 0,1. Найти натяжение нити, к которой прикреплена вторая гиря.
2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m1=m2=1 кг соединены нитью, перекинутой через блок (рис. 1). Коэффициент трения одной из гирь о стол равен 0,1. Найти натяжение нити, к которой прикреплена вторая гиря. 3. Из пушки (рис. 2) выпустили последовательно два снаряда со скоростью v0=300 м/с: первый – под углом a1=450 к горизонту, второй – под углом a2=300 к горизонту. Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.
3. Из пушки (рис. 2) выпустили последовательно два снаряда со скоростью v0=300 м/с: первый – под углом a1=450 к горизонту, второй – под углом a2=300 к горизонту. Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом. . Определить модуль полного ускорения тела в момент времени t=2 с.
. Определить модуль полного ускорения тела в момент времени t=2 с. 5. Две прочные линейки расположены параллельно друг другу на расстоянии d=2см под углом a=50 к горизонту (рис. 3). С каким ускорением будет катиться по ним шарик, радиус которого r=1,5 см? Скольжение отсутствует.
5. Две прочные линейки расположены параллельно друг другу на расстоянии d=2см под углом a=50 к горизонту (рис. 3). С каким ускорением будет катиться по ним шарик, радиус которого r=1,5 см? Скольжение отсутствует. 8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м (рис. 4). Определить период малых колебаний диска относительно точки А. Ось перпендикулярна плоскости диска.
8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м (рис. 4). Определить период малых колебаний диска относительно точки А. Ось перпендикулярна плоскости диска. 2. Человек находится на расстоянии S=50 м от прямой дороги (рис. 1), по которой приближается автомобиль со скоростью v1=10 м/с. По какому направлению должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S1=200 м от человека и если человек может бежать со скоростью v2=3 м/с?
2. Человек находится на расстоянии S=50 м от прямой дороги (рис. 1), по которой приближается автомобиль со скоростью v1=10 м/с. По какому направлению должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S1=200 м от человека и если человек может бежать со скоростью v2=3 м/с? 3. Небольшое тело заставили двигаться снизу вверх по наклонной плоскости, составляющей угол a=150 с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в n=2,0 раза меньше времени спуска (рис. 2).
3. Небольшое тело заставили двигаться снизу вверх по наклонной плоскости, составляющей угол a=150 с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в n=2,0 раза меньше времени спуска (рис. 2). 4. Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиуса R=40 м (рис. 3). Полотно дороги составляет угол α=200 с горизонтальной плоскостью. Каково ускорение автомобиля, движущегося с постоянной по модулю скоростью v=72 км/ч?
4. Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиуса R=40 м (рис. 3). Полотно дороги составляет угол α=200 с горизонтальной плоскостью. Каково ускорение автомобиля, движущегося с постоянной по модулю скоростью v=72 км/ч? 5. Вертикальный столб высотой h=5 м подпиливается у основания и падает на Землю (рис. 4). Определить линейную скорость его верхнего конца в момент удара о Землю.
5. Вертикальный столб высотой h=5 м подпиливается у основания и падает на Землю (рис. 4). Определить линейную скорость его верхнего конца в момент удара о Землю. 8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Определить период малых колебаний диска относительно точки В. Ось перпендикулярна плоскости диска.
8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Определить период малых колебаний диска относительно точки В. Ось перпендикулярна плоскости диска. Вариант № 8
Вариант № 8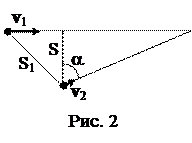 2. Человек находится на расстоянии S=50 м от прямой дороги, по которой приближается автомобиль со скоростью v1=10м/с (рис. 2). Определить наименьшую скорость, с которой должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S1=200 м от человека.
2. Человек находится на расстоянии S=50 м от прямой дороги, по которой приближается автомобиль со скоростью v1=10м/с (рис. 2). Определить наименьшую скорость, с которой должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S1=200 м от человека. д) v2=2,5 м/с.
д) v2=2,5 м/с. образует с вектором скорости
образует с вектором скорости  угол α=450.
угол α=450.
 8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Каково будет отношение периодов колебаний этого диска вокруг оси перпендикулярной к плоскости диска, проходящей через точку А и В?
8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×103 кг/м3), вторая – свинцовая (плотность r=10×103 кг/м3) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Каково будет отношение периодов колебаний этого диска вокруг оси перпендикулярной к плоскости диска, проходящей через точку А и В? 1. Камень, брошенный со скоростью 12 м/с под углом 45о к горизонту (рис. 1), упал на землю на расстоянии L от места бросания. С какой высоты надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место?
1. Камень, брошенный со скоростью 12 м/с под углом 45о к горизонту (рис. 1), упал на землю на расстоянии L от места бросания. С какой высоты надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место? 2. Наблюдатель, стоявший в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за время t=4 с. Сколько времени будет двигаться мимо наблюдателя 7 – й вагон? Движение считать равномерно ускоренным.
2. Наблюдатель, стоявший в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за время t=4 с. Сколько времени будет двигаться мимо наблюдателя 7 – й вагон? Движение считать равномерно ускоренным. 5. Массивное колесо, насаженное на оси, поддерживается двумя закрепленными нитями (рис. 3). Ось вращения колеса горизонтальна. Нити постепенно раскручиваются с оси, а колесо опускается. Определить натяжение F каждой из двух нитей, если масса колеса вместе с осью m=1 кг, момент инерции относительно этой оси I=2,5×10-3 кг×м2 и радиус оси r=5 мм.
5. Массивное колесо, насаженное на оси, поддерживается двумя закрепленными нитями (рис. 3). Ось вращения колеса горизонтальна. Нити постепенно раскручиваются с оси, а колесо опускается. Определить натяжение F каждой из двух нитей, если масса колеса вместе с осью m=1 кг, момент инерции относительно этой оси I=2,5×10-3 кг×м2 и радиус оси r=5 мм. ; y=coswt. Найти уравнение траектории точки.
; y=coswt. Найти уравнение траектории точки. 8. Физический маятник состоит из стержня квадратного сечения, подвешенного за конец, и груза, прикрепленного на другом конце (рис. 4). Груз имеет форму куба с ребром а=40 см, а стержень – длину ℓ=400 мм и сторону сечения b=4 мм; груз и стержень сделаны из одного материала. Найти приближенное значение периода колебаний Т такого маятника (при расчете можно полагать стержень достаточно тонким).
8. Физический маятник состоит из стержня квадратного сечения, подвешенного за конец, и груза, прикрепленного на другом конце (рис. 4). Груз имеет форму куба с ребром а=40 см, а стержень – длину ℓ=400 мм и сторону сечения b=4 мм; груз и стержень сделаны из одного материала. Найти приближенное значение периода колебаний Т такого маятника (при расчете можно полагать стержень достаточно тонким). 1. Наклонная плоскость составляет угол 37° с линией горизонта. На наклонной плоскости лежит брусок массой m1=1 кг. Шнур, привязанный одним концом к бруску, перекинут через неподвижный блок, укрепленный в верхнем конце наклонной плоскости. К другому концу шнура, свисающему с блока, подвешена гирька массой m2=0,4 кг (рис. 1). Коэффициент трения равен 0,2. С каким ускорением будет двигаться брусок? В начальный момент скорость равна нулю.
1. Наклонная плоскость составляет угол 37° с линией горизонта. На наклонной плоскости лежит брусок массой m1=1 кг. Шнур, привязанный одним концом к бруску, перекинут через неподвижный блок, укрепленный в верхнем конце наклонной плоскости. К другому концу шнура, свисающему с блока, подвешена гирька массой m2=0,4 кг (рис. 1). Коэффициент трения равен 0,2. С каким ускорением будет двигаться брусок? В начальный момент скорость равна нулю. 2. Наблюдатель, стоящий на платформе, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение t1=4 с, а второй – в течение t2=5 с. После этого передний край поезда остановился на расстоянии S=75 м от наблюдателя. Считая движение поезда равномерно замедленным, определить его ускорение.
2. Наблюдатель, стоящий на платформе, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение t1=4 с, а второй – в течение t2=5 с. После этого передний край поезда остановился на расстоянии S=75 м от наблюдателя. Считая движение поезда равномерно замедленным, определить его ускорение.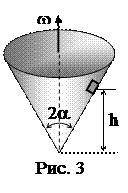 4. На внутренней поверхности конической воронки с углом 2a (a=300) при вершине на высоте h=0,1 м от вершины находится малое тело. Коэффициент трения между телом и поверхностью воронки равен k=0,1. Найти минимальную угловую скорость вращения конуса вокруг вертикальной оси, при которой тело будет неподвижно в воронке (рис. 3).
4. На внутренней поверхности конической воронки с углом 2a (a=300) при вершине на высоте h=0,1 м от вершины находится малое тело. Коэффициент трения между телом и поверхностью воронки равен k=0,1. Найти минимальную угловую скорость вращения конуса вокруг вертикальной оси, при которой тело будет неподвижно в воронке (рис. 3).


