
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затраты времени на обработку деталиСодержание книги
Поиск на нашем сайте
Определить средние затраты времени на обработку детали:
Если данные представлены в виде интервального ряда распределения, то принцип расчета средней остается прежним, но предварительно вычисляется среднее значение признака для каждого интервала, представляющее полусумму нижнего и верхнего значений интервала где
Если есть интервалы с открытыми границами, то для первой группы величина интервала берется равной величине интервала последующей группы. Пример. Таблица 14 Стаж работы рабочих цеха
Определить средний стаж рабочих цеха. Он равен:
Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Она бывает простая и взвешенная: Простая – Пример. Определить среднюю скорость движения автомобиля, если известно, что три машины прошли один путь, при этом одна машина двигалась со скоростью 60 км/ч, вторая – 70 км/ч, третья – 100 км/ч.
Взвешенная – Пример. Определить среднюю себестоимость изготовления единицы продукции.
Средняя квадратическая используется в том случае, когда необходимо возводить варианты в квадрат: Простая – Взвешенная – Средняя квадратическая применяется в технике, а также в математическом анализе. Средняя геометрическая – Данный вид средних применяется для анализа средних показателей динамики. Средняя хронологическая: Простая – Применяется в том случае, когда интервалы времени между явлениями равны. Пример. Определить средний остаток материалов на складе за I квартал текущего года, если известно, что остаток на 1-ое января составил 24,8 млн. руб., на 1-ое февраля – 25,6 млн. руб., на 1-ое марта – 21,2 млн. руб., на 1-ое апреля – 18,1 млн. руб.
взвешенная – Применяется в том случае, когда интервалы времени между явлениями неравны. Пример. Определить средний остаток краски на складе за десять дней марта, если известно, что остаток краски на 1 марта составил 200 кг, 3-его марта отпущено в производство 70 кг, 5-го марта поступило от поставщика 100 кг, 9-го марта списано в производство 50 кг краски.
Свойства средней арифметической: 1. Средняя арифметическая из постоянных чисел равна этому постоянному числу. Пусть х = a, тогда: 2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится. Пусть f уменьшим в к раз. Тогда: 3. Если все варианты уменьшить или увеличить на какое-либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же. Уменьшим все варианты х на а, т.е.
Среднюю арифметическую первоначального ряда можно получить, прибавляя к средней арифметической нового ряда, ранее вычтенное из вариантов число a, т.е. 4. Если все варианты уменьшить в к раз, то средняя арифметическая нового ряда уменьшится в к раз. Пусть Среднюю арифметическую первоначального ряда можно получить, увеличив среднюю арифметическую нового ряда в 5. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю.
Перечисленные свойства позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты на какое-либо число а, сокращать их в к раз и рассчитывать среднюю арифметическую из уменьшенных вариантов, а затем переходить к средней первоначального ряда. Способ исчисления средней арифметической с использованием ее свойств известен в статистике как способ «условного нуля» или «условной средней», а также как «способ моментов». Этот способ расчета находит отражение в следующей формуле:
Если уменьшенные варианты Пример. Используя метод моментов, определить средний объем реализованной продукции:
Для характеристики среднего значения признака в вариационном ряду используется не только средняя арифметическая, но и мода и медиана, котороые относятся к структурным средним. Мода – это наиболее часто встречающееся значение признака в совокупности. Медианой называется численное значение признака, расположенное в середине ранжированного ряда, которое делит этот ряд на две равные по численности части. Для определения медианы сначала находят ее место в ряду по формуле Применяется мода при экспертных оценках, при установлении размера изделий, который пользуется наибольшим спросом (одежда, обувь), медиана используется при статистическом контроле качества продукции. Пример. Таблица 15
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.01 с.) |

 .
. ,
, ;
; – нижняя граница интервала;
– нижняя граница интервала;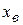 – верхняя граница интервала.
– верхняя граница интервала. .
. ;
; км/ч.
км/ч.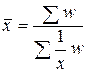 ,
,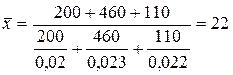 руб.
руб. ;
; .
.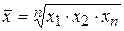 .
. ;
;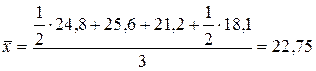 млн. руб.
млн. руб.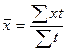 .
. кг.
кг.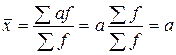 .
. .
. . Тогда:
. Тогда: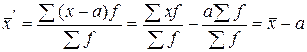 .
. .
. , тогда
, тогда 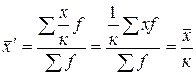 .
. раз:
раз:  ,
,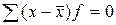 .
.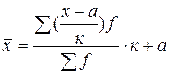 .
.
 обозначить через
обозначить через  , то
, то  .
.
 ,
а =225
,
а =225
 ,
к =50
,
к =50
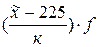
 млн. руб.
млн. руб.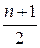 , где n – число членов ряда (
, где n – число членов ряда (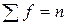 ). Если число единиц четное, то место медианы в ряду определяется как
). Если число единиц четное, то место медианы в ряду определяется как  .
.


