
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т.Ф. Манцерова, Ю.К. АбуховичСодержание книги
Поиск на нашем сайте
Т.Ф. Манцерова, Ю.К. Абухович
Социально-экономическая
Курс лекций
Минск
М24
Серия основана в 2001 году Рекомендовано к изданию Комиссией по приемке и аттестации электронных версий учебных и учебно-методических материалов Академии управления при Президенте Республики Беларусь.
СОДЕРЖАНИЕ ПРЕДИСЛОВИЕ 5 ТЕМА 1. ПРЕДМЕТ И МЕТОД СТАТИСТИЧЕСКОЙ НАУКИ. ЗАДАЧИ И ОРГАНИЗАЦИЯ СТАТИСТИКИ В РЕСПУБЛИКЕ БЕЛАРУСЬ 7 Лекция 1. Предмет и метод статистической науки. Задачи и организация статистики в Республике Беларусь 7 Контрольные вопросы к теме №1 15 ТЕМА 2. ТЕОРИЯ СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ 16 Лекция 2. Теория статистического наблюдения 16 Контрольные вопросы к теме №2 27 ТЕМА 3. СВОДКА И ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ И ГРАФИКИ 28 Лекция 3. Сводка и группировка статистических данных 28 Контрольные вопросы к лекции №3 39 Лекция 4. Статистические таблицы и графики 40 Контрольные вопросы к лекции №4 48 ТЕМА 4. ТЕОРИЯ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ 49 Лекция 5. Теория статистических показателей 49 Контрольные вопросы к теме №4 60 ТЕМА 5. ТЕОРИЯ СРЕДНИХ ВЕЛИЧИН 61 Лекция 6. Теория средних величин 61 Контрольные вопросы к теме №5 73 ТЕМА 6. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ 73 Лекция 7. Статистическое изучение динамики социально-экономических явлений 73 Контрольные вопросы к теме №6 88 ТЕМА 7. ИНДЕКСНЫЙ МЕТОД В СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЯХ 89 Лекция 8. Индексный метод в статистических исследованиях 89 Контрольные вопросы к теме №7 101 ТЕМА 8. МАКРОЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ ПРОИЗВОДСТВА ТОВАРОВ И УСЛУГ 102 Лекция 9. Макроэкономические показатели производства товаров и услуг 102 Контрольные вопросы к теме №8 115 ТЕМА 9. ПОКАЗАТЕЛИ ОБРАЗОВАНИЯ И РАСПРЕДЕЛЕНИЯ ДОХОДОВ 116 Лекция 10. Показатели образования и распределения доходов 116 Контрольные вопросы к теме №9 127 ТЕМА 10. ПОКАЗАТЕЛИ ИСПОЛЬЗОВАНИЯ ДОХОДОВ И НАКОПЛЕНИЯ 128 Лекция 11. Показатели использования доходов и накопления 128 Контрольные вопросы к теме №10 134 ТЕМА. 11. СТАТИСТИКА НАЦИОНАЛЬНОГО БОГАТСТВА 135 Лекция 12. Статистика национального богатства 135 Контрольные вопросы к теме №11 151 ТЕМА 12. СТАТИСТИКА НАСЕЛЕНИЯ, ТРУДОВЫХ РЕСУРСОВ И ЗАНЯТОСТИ 152 Лекция 13. Статистика населения, трудовых ресурсов и занятости 152 Контрольные вопросы к теме №12 167 ТЕМА 13. СТАТИСТИКА УРОВНЯ ЖИЗНИ И ПОТРЕБЛЕНИЯ НАСЕЛЕНИЯ 169 Лекция 14. Статистика уровня жизни и потребления населения 169 Контрольные вопросы к теме №13 189 ТЕМА 14. СТАТИСТИКА ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ ЭКОНОМИКИ 191 Лекция 15. Статистика эффективности функционирования экономики 191 Контрольные вопросы к теме №14 199 ЛИТЕРАТУРА 200
ПРЕДИСЛОВИЕ В современных условиях развития экономики Республики Беларусь все большее значение приобретают проблемы совершенствования методов управления. Развитие межпроизводственных связей охватывает широкий комплекс взаимоотношений правового, финансового и экономического характера. Данные вопросы решаются, прежде всего, учетно-экономическими службами. В этой связи изучение курса «Социально-экономическая статистика» крайне важно для подготовки высококвалифицированных специалистов в сфере экономики. Статистика вооружает управленцев мощным орудием социально–экономического познания и управления. Без статистических исследований деятельности предприятия, отрасли и всего народного хозяйства невозможно обоснование и анализ как внешней, так и внутренней стратегии государства в области экономики. Основная цель пособия – ознакомить студентов с общими методами и принципами статистики, понятийным аппаратом, основными категориями и методологией статистики, помочь разобраться в методологии исчисления и анализа показателей системы национальных счетов, оценки уровня жизни населения, эффективности функционирования экономики. Данное пособие составлено таким образом, что сначала излагаются темы общей теории статистики, а затем – социально-экономической, что весьма удобно при его использовании в учебном процессе. В первых семи темах излагается материал по статистической теории и методологии. В нем рассмотрены основные методы статистического исследования, теория статистического показателя, теория средних величин, анализ динамики социально-экономических показателей, индексный метод анализа. Во многих темах есть примеры расчета. В темах, посвященных основам социально-экономической статистики, рассмотрены основы расчета основных макроэкономических показателей в соответствии с международным стандартом СНС-93. Таблица 4 К трудовой деятельности
Интервалы групп могут быть закрытыми, когда указаны нижняя и верхняя границы (табл.9). Таблица 9 Пример. По состоянию на 14 октября имеются следующие данные о расходе металла 8 рабочими (кг): 17,2; 19,0; 20,0; 17,0; 18,0; 19,8; 18,0; 18,6 Для того чтобы определить средний расход металла на одного рабочего, необходимо общий расход металла разделить на число рабочих:
Если данные представлены в виде дискретного ряда распределения, то расчет средней производится по формуле средней арифметической взвешенной: где х – значение признака; f – частота повторения соответствующего признака (веса). Пример. Таблица 13 Стаж работы рабочих цеха
Определить средний стаж рабочих цеха. Он равен:
Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Она бывает простая и взвешенная: Простая – Пример. Определить среднюю скорость движения автомобиля, если известно, что три машины прошли один путь, при этом одна машина двигалась со скоростью 60 км/ч, вторая – 70 км/ч, третья – 100 км/ч.
Взвешенная – Пример. Определить среднюю себестоимость изготовления единицы продукции.
Средняя квадратическая используется в том случае, когда необходимо возводить варианты в квадрат: Простая – Взвешенная – Средняя квадратическая применяется в технике, а также в математическом анализе. Средняя геометрическая – Данный вид средних применяется для анализа средних показателей динамики. Средняя хронологическая: Простая – Применяется в том случае, когда интервалы времени между явлениями равны. Пример. Определить средний остаток материалов на складе за I квартал текущего года, если известно, что остаток на 1-ое января составил 24,8 млн. руб., на 1-ое февраля – 25,6 млн. руб., на 1-ое марта – 21,2 млн. руб., на 1-ое апреля – 18,1 млн. руб.
взвешенная – Применяется в том случае, когда интервалы времени между явлениями неравны. Пример. Определить средний остаток краски на складе за десять дней марта, если известно, что остаток краски на 1 марта составил 200 кг, 3-его марта отпущено в производство 70 кг, 5-го марта поступило от поставщика 100 кг, 9-го марта списано в производство 50 кг краски.
Свойства средней арифметической: 1. Средняя арифметическая из постоянных чисел равна этому постоянному числу. Пусть х = a, тогда: 2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится. Пусть f уменьшим в к раз. Тогда: 3. Если все варианты уменьшить или увеличить на какое-либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же. Уменьшим все варианты х на а, т.е.
Среднюю арифметическую первоначального ряда можно получить, прибавляя к средней арифметической нового ряда, ранее вычтенное из вариантов число a, т.е. 4. Если все варианты уменьшить в к раз, то средняя арифметическая нового ряда уменьшится в к раз. Пусть Среднюю арифметическую первоначального ряда можно получить, увеличив среднюю арифметическую нового ряда в 5. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю.
Перечисленные свойства позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты на какое-либо число а, сокращать их в к раз и рассчитывать среднюю арифметическую из уменьшенных вариантов, а затем переходить к средней первоначального ряда. Способ исчисления средней арифметической с использованием ее свойств известен в статистике как способ «условного нуля» или «условной средней», а также как «способ моментов». Этот способ расчета находит отражение в следующей формуле:
Если уменьшенные варианты Пример. Используя метод моментов, определить средний объем реализованной продукции:
Для характеристики среднего значения признака в вариационном ряду используется не только средняя арифметическая, но и мода и медиана, котороые относятся к структурным средним. Мода – это наиболее часто встречающееся значение признака в совокупности. Медианой называется численное значение признака, расположенное в середине ранжированного ряда, которое делит этот ряд на две равные по численности части. Для определения медианы сначала находят ее место в ряду по формуле Применяется мода при экспертных оценках, при установлении размера изделий, который пользуется наибольшим спросом (одежда, обувь), медиана используется при статистическом контроле качества продукции. Пример. Таблица 15 Производство пиломатериалов
Особенностью интервальных рядов динамики является то, что данные этих рядов можно суммировать и получать новые численные значения, относящиеся к более длительным периодам времени. Моментный ряд динамики состоит из показателей, характеризующих состояние явления на определенные моменты времени. Таблица 18 Запас топлива на складах
Уровни моментных рядов складывать нельзя, так как слагающие явления единицы последовательно повторяются в различных уровнях ряда, поэтому их сумма не имеет смысла. К суммированию показателей интервального ряда часто прибегают для построения рядов динамики с нарастающими итогами. Таблица 19 Добыча угля за январь-июль
Нарастающие итоги часто приводятся в отчетах предприятий. Если ряд динамики состоит из относительных или средних величин, то суммировать их нельзя, но разность их имеет реальный смысл. Таблица 20 Понятие и виды индексов.
Индексы являются важнейшим видом обобщающих статистических показателей. Они используются для характеристики динамики явлений, сравнений по различным территориям, при контроле и разработке плановых заданий. Наравне со средними величинами они представляют собой один из самых распространенных видов статистических показателей. Слово «индекс» (index) в переводе с латыни означает указатель, показатель. В статистике этот термин имеет специфическое значение. Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом. Индекс является результатом сравнения двух одноименных величин, поэтому необходимо различать величину сравнения (числителя индексного отношения) и базу сравнения (знаменатель). Выбор базы сравнения определяется целью исследования; при изучении динамики в качестве базы используются данные какого-либо предыдущего периода; при контроле за выполнением плана – плановые данные; при территориальных сравнениях – данные другой территории. Величину сравнения обычно называют показателем отчетного периода, базу сравнения называют показателем базисного периода. Если базисный уровень при исчислении индекса принимается за единицу, то индексы вычисляются в виде коэффициентов, а если базисный уровень принимается за 100, то индекс вычисляют в виде процентов. На основании вычисления можно определить, во сколько раз отчетная величина больше или меньше базисной или на сколько процентов она больше или меньше базисной. Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых. Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции. При всем их разнообразии экономические индексы подразделяются на индивидуальные и общие индексы. Индивидуальным называется индекс, характеризующий изменение объема производства, объема продажи, уровня производительности труда и т.д. в отношении какого-нибудь одного продукта. Например, имеются следующие данные о производстве электродвигателей переменного тока с высотой оси вращения 63 – 450 мм (тыс.шт.) в 2006 – 448; в 2007 – 188. Определим индивидуальный индекс физического объема продукции:
Индивидуальные индексы: · цен · себестоимости · стоимости Цепные и базисные индексы
3.Средние индексы и их виды. Агрегатный способ исчисления общих индексов является основным, но не единственным в статистике. В ряде случаев из-за отсутствия некоторых данных нельзя произвести расчет по формуле агрегатного индекса. Это может иметь место в том случае, если нет данных об абсолютном значении индексируемой величины, т.е. величины показателя, характеризующего ту сторону явления, изменение которой изучается (например, при исчислении индекса физического объема продукции нет данных об объеме производства в целом). В этом случае применяются средние индексы. Мы знаем, что индивидуальный индекс физического объема выражается
Пример. Таблица 25
Определить общий индекс физического объема продукции.
В тех случаях, когда нет данных о количестве проданных товаров, нельзя исчислить агрегатный индекс цен, но если известны индивидуальные индексы цен, а также имеются данные о продажах в текущем периоде в ценах текущего периода, таким образом, можно исчислить средний гармонический индекс цен. Из формулы индивидуального индекса цен Пример. Таблица 26
Определить общий индекс цены:
(цены снижены на 7,4%). ТЕМА 9. ПОКАЗАТЕЛИ ОБРАЗОВАНИЯ И РАСПРЕДЕЛЕНИЯ ДОХОДОВ Лекция 10. Показатели образования и распределения доходов Основные понятия: первичные доходы; валовая заработная плата; оплата труда в натуральной форме; отчисления на социальные нужды; налоги на производство; расчет ВВП распределительным методом; валовая прибыль экономики; чистая прибыль экономики; чистый национальный располагаемый доход; доход от собственности; компенсация наемным работникам-резидентам; рента; проценты; дивиденды; валовой национальный доход (ВНД). Показатели образования доходов. Определение валового внутреннего продукта распределительным методом. Располагаемого дохода
Скорректированный валовой располагаемый доход институциональных единиц и секторов или скорректированный валовой национальный располагаемый доход по экономике страны в целом переносятся в данный счет из счета перераспределения доходов в натуральной форме, рассмотренного выше, и записываются в ресурсной части. В использовании ресурсов показываются фактическое конечное потребление товаров и услуг и балансирующая статья счета, которой является сбережение. В фактическом конечном потреблении товаров и услуг, т.е. их непосредственном использовании для удовлетворения текущих индивидуальных потребностей людей и коллективных потребностей общества, участвуют институциональные единицы двух секторов экономики, а именно сектора домашних хозяйств и общего государственного управления. Фактическое конечное потребление домашних хозяйств-резидентов включает стоимость потребительских товаров и услуг, реально полученных ими для индивидуального потребления, независимо от того, кто их финансирует (оплачивает). Поэтому фактическое конечное потребление домашних хозяйств определяется путем суммирования: 1) расходов домашних хозяйств на конечное потребление, т.е. покупку ими потребительских товаров и услуг; 2) стоимости потребительских товаров и услуг, полученных домашними хозяйствами в виде социальных трансфертов в натуральной форме от органов государственного управления и от некоммерческих организаций, обслуживающих домашние хозяйства. Эти трансферты количественно равны сумме расходов на индивидуальное конечное потребление органов государственного управления и расходов на конечное потребление некоммерческих организаций, обслуживающих домашние хозяйства. Фактическое конечное потребление органов общего государственного управления принимается равным стоимости их расходов на товары и услуги коллективного потребления. Очевидно, что общая стоимость социальных трансфертов, полученных домашними хозяйствами–резидентами равна стоимости социальных трансфертов, выплаченных органами общего государственного управления и некоммерческими организациями. Следовательно, фактическое конечное потребление для всей экономики будет равно сумме расходов на конечное потребление товаров и услуг. При этом балансирующая статья «Сбережение» должна быть идентичной по охвату и стоимости в счетах использования располагаемого дохода и использования скорректированного располагаемого дохода, так как социальные трансферты в натуральной форме одинаково влияют на показатели располагаемого дохода и конечного потребления в этих счетах. Контрольные вопросы к теме №10 1. Показатели использования располагаемого дохода. 2. Какие расходы включаются в расходы на конечное потребление домашних хозяйств? 3. Что включает в себя валовое конечное потребление? 4. Определение ВВП методом конечного использования. 5. Порядок распределения скорректированного располагаемого дохода. Возраст, лет
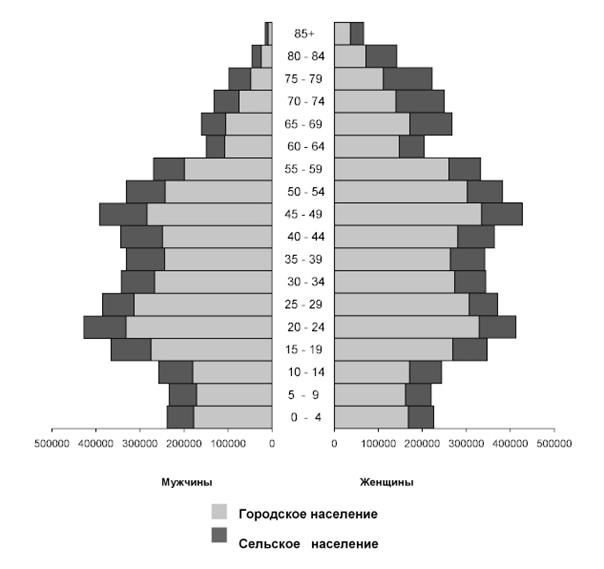
Рис.14 Половозрастная пирамида населения Республики Беларусь (на 1 января 2008 г.; человек)
Численность населения непрерывно изменяется вследствие рождаемости и смертности, а также вследствие пространственного перемещения населения. Численность населения определяется по состоянию на определенный момент времени, т.е. в результате переписей. Перепись является в настоящее время основным методом точного определения численности населения.
Рис. 15 Виды переписей
Однако переписи населения проводятся относительно редко, а данные о численности населения требуются постоянно. Поэтому в периоды между переписями статистические органы проводят, так называемую, текущую оценку численности населения, т.е. проводят расчет, опираясь на данные последней переписи и материалы текущей статистики о движении населения. Ее расчеты уточняются на основании итогов очередной переписи. Различают две категории населения, учитываемые при проведении переписей населения: постоянное поселение и наличное население. К постоянному населению относятся лица, которые обычно проживают в данном населенному пункте, а к наличному – все лица, находившиеся на критический момент переписи на данной территории, независимо от того, постоянно они здесь проживают или временно. Чтобы определить численность постоянного населения, в процессе переписи производится учет временно отсутствующих и временно проживающих. Временно отсутствующими считаются постоянные жители данного населенного пункта, временно выбывшие из него. Таким образом, временно отсутствующие есть часть постоянного населения. Временно проживающие составляют часть наличного населения. Численность постоянного населения можно определить:
где
Большое значение в статистике населения имеет показатель средней численности населения. Средняя численность населения может быть рассчитана разными методами. Наиболее точным является метод прожитых населением человеко-лет. В данном случае определяется общее число прожитых данным населением человеко-лет за изучаемый период времени и делится на длину этого периода. Часто среднюю годовую численность населения определяют как полусумму численности его на начало и конец года:
где
При наличии данных за несколько равностоящих одна от другой дат расчет
Если же временное расстояние между датами неодинаковое, то расчет проводится по формуле средней арифметической (хронологической) взвешенной:
где
Численность населения на конец года рассчитывается по формуле:
где N − число родившихся; М − число умерших; П − численность прибывших в данный населенный пункт; В − численность выбывших из данного населенного пункта. В межпереписной период перспективную численность населения рассчитывают, используя коэффициенты общего прироста за периоды, предшествующие прогнозируемому. Один из методов расчета перспективной численности населения:
где Кобщ − коэффициент общего прироста населения; S0 − численность населения на начало года; N − число периодов прогнозов. Для расчета изменения численности населения во времени рассчитывают показатели динамики. Население является главным материальным компонентом общества, и изучение закономерностей его развития имеет большое значение для экономики страны. Для каждой отдельно взятой страны общая численность населения может меняться за счет двух факторов: · естественного движения (рождаемости и смертности); · миграционного (механического) движения. Однако меняется не только общая численность населения, но и состав. В настоящее время в статистике используются четыре взаимодополняющих источника данных о населении: · переписи населения; · текущий учет естественного движения населения и его миграции; · выборочные и специальные демографические обследования; · регистры и различные учеты населения. Данные этих источников используются для различных целей и не могут заменять друг друга. Однако между ними существует тесная связь: каждый источник дополняет или продолжает другой. Основным источником данных о населении является перепись, которая проводится один раз в 10 лет. Учет населения при ее проведении осуществляется по населенным пунктам по состоянию на определенный момент времени, который называется критическим моментом. В 1853 г. были сформированы принципы проведения переписи, основные из которых используются до сих пор. При характеристике динамики численности населения нужно учитывать два обстоятельства: 1) можно сравнивать между собой население только одной категории (либо постоянное, либо наличное); 2) если были административно-территориальные изменения, то данные о численности населения должны быть сопоставимы в отношении территории. Общий абсолютный прирост населения (
где
При этом: где
Тогда: Как общий, так и естественный, и миграционные приросты могут быть положительными или отрицательными. Абсолютные приросты – это интервальные показатели, они рассчитываются за определенные периоды времени (наибольшее значение имеют годовые показатели). Данные о численности населения представляются в территориальном разрезе (в пределах административно-территориальных единиц). Для характеристики размещения населения используются структурные показатели. Это: 1) доли населения, проживающего в отдельных регионах; 2) показатель физической плотности населения, который рассчитывается как отношение численности населения к занимаемой им площади (самая большая плотность населения – 15539 чел. на 1 км2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.014 с.) |

 ББК 60.6
ББК 60.6 Рецензенты: кандидат экономических наук, доцент Е.И.Сапелкина
Рецензенты: кандидат экономических наук, доцент Е.И.Сапелкина  кг.
кг. ,
, .
. ;
; км/ч.
км/ч.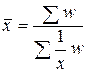 ,
,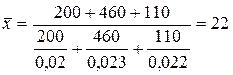 руб.
руб. ;
; .
.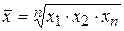 .
. ;
;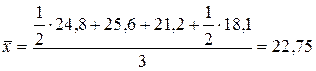 млн. руб.
млн. руб.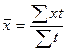 .
. кг.
кг.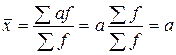 .
. .
. . Тогда:
. Тогда: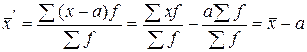 .
. .
. , тогда
, тогда 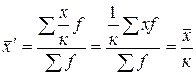 .
. раз:
раз:  ,
,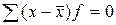 .
.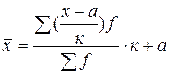 .
.
 обозначить через
обозначить через  , то
, то  .
.
 ,
а =225
,
а =225
 ,
к =50
,
к =50
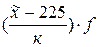
 млн. руб.
млн. руб.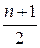 , где n – число членов ряда (
, где n – число членов ряда (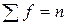 ). Если число единиц четное, то место медианы в ряду определяется как
). Если число единиц четное, то место медианы в ряду определяется как  .
. ;
; 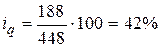 , т.е. произошло снижение объема производства на 58%.
, т.е. произошло снижение объема производства на 58%. ;
; ;
;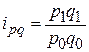 .
.
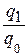 ;
;  ;
;  ;
; 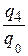
 ;
;  ;
; 

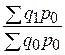 ;
;  ;
;  ;
;
 ;
;  ;
;

 ;
;  ;
;  ;
; 
 ;
;  ;
; 

 ;
;  ;
; 
 ;
; 

 ;
;  ;
; 
 ;
; 

 ;
;  ;
; 
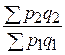 ;
; 
 . Если в формуле агрегатного индекса
. Если в формуле агрегатного индекса  заменить
заменить  на выражение
на выражение  , то получим формулу среднего арифметического индекса физического объема:
, то получим формулу среднего арифметического индекса физического объема:
 .
. (объем выпуска увеличился на 22,7%).
(объем выпуска увеличился на 22,7%). . Если в агрегатном индексе цен
. Если в агрегатном индексе цен  заменить в знаменателе
заменить в знаменателе  на
на  , то получим формулу среднего гармонического индекса цен:
, то получим формулу среднего гармонического индекса цен:  .
.

 ,
, – наличное население;
– наличное население; – временно отсутствующие;
– временно отсутствующие; – временно прибывшие.
– временно прибывшие. ,
, – численность населения на начало года;
– численность населения на начало года; – численность населения на конец года.
– численность населения на конец года. может быть произведен по формуле средней хронологической простой:
может быть произведен по формуле средней хронологической простой: .
. , или
, или ,
, − средняя численность населения i-го периода;
− средняя численность населения i-го периода; − длительность i -го периода времени.
− длительность i -го периода времени. ,
, − численность населения на начало года;
− численность населения на начало года; ,
, ):
): или
или  ,
, – естественный прирост;
– естественный прирост; – механический прирост.
– механический прирост. ;
; 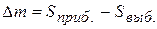 ,
, – число родившихся;
– число родившихся; – число умерших;
– число умерших; – число прибывших;
– число прибывших; – число выбывших.
– число выбывших.



